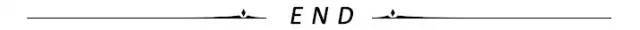考生对满分的向往,就是我们的奋斗目标!!
还记得上次我们留给大家的弹性力学填空题吗?今天给大家提供参考答案。
弹性力学重要公式复习检测(请填空)
弹性力学重要公式总结(含答案)
弹性力学的基本方程(空间直角坐标)
1. 平衡微分方程:(3个)
【参考答案】

2. 几何方程(6个)
【参考答案】

3. 物理方程:(6个)
【参考答案】

4. 用应变表示应力(6个)
【参考答案】

按位移求解:
5. 弹性方程(6个)(用位移表示应力)
【参考答案】

6.拉梅方程:(3个)
【参考答案】
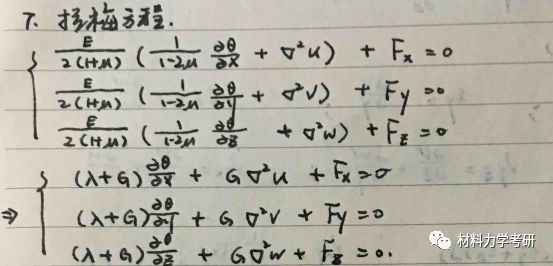
按应力求解:
7.用应变表示的协调方程:
(1)相同平面变形协调:(3个)
(2)不同平面变形协调:(3个)
【参考答案】

8. 常体力下用应力表示的协调方程:(6个)
【参考答案】

9. 斜截面上一点的应力状态(空间):(3个)
法向应力:
切向应力:
正应变:
【参考答案】
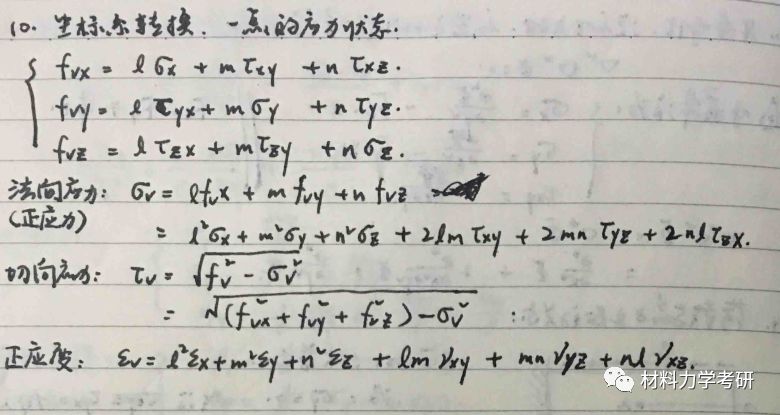
10. 应力函数法(平面问题)求解步骤,应力分量的表示:
1)校验应力函数是否满足相容方程: ;
2)求应力分量:(3个)
3)校验边界条件,大边界精确满足,小边界满足圣维南原理;
4)多连体满足位移单值条件。
【参考答案】

11. 直角坐标系中,斜截面上的边界条件:(2个)(注意符号方向)
【参考答案】

半逆解法
12. 直角坐标下的双调和方程(相容方程): 。
直角坐标下的应力用应力函数表示:(3个)(考虑体力)
【参考答案】
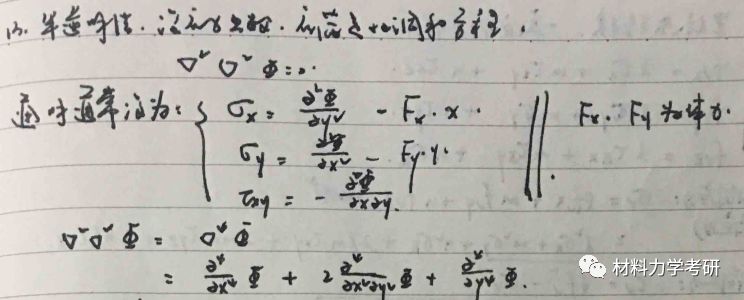
13. 荷载与应力函数间的关系:(怎么设?应力函数形式?)
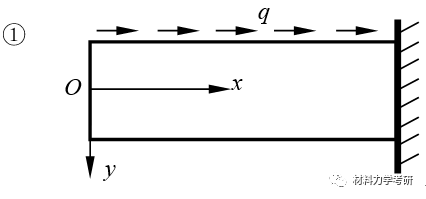
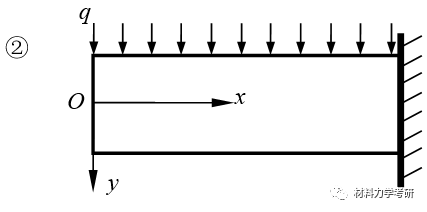
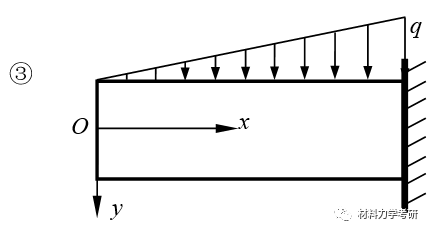
【参考答案】

14. 极坐标系下的平衡微分方程(平面问题):(2个)
【参考答案】

15. 极坐标系下几何方程:(3个)
16. 极坐标系下物理方程:(3个)(平面应力问题)
17. 极坐标系下的双调和方程(相容方程): 。
极坐标下的应力用应力函数表示:(3个)(不考虑体力)
应力轴对称情况
18. 应力函数(1个)(平面应力)
应力分量为:(3个)
*位移分量为:(2个)
位移轴对称情况
19. 位移轴对称情况是应力轴对称的特殊情况,应力函数为?(1个)(平面应力)
应力分量:(3个)
位移分量:(2个)
【15~19参考答案】


20. 应力分量的坐标转换:
(1)极坐标转直角坐标:(3个)
(2)直角坐标转极坐标:(3个)
【参考答案】

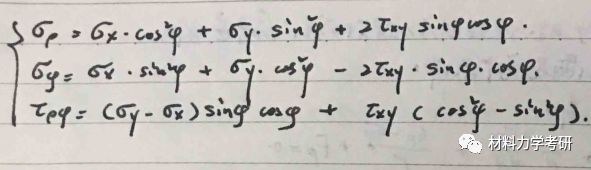
21. 位移分量的坐标转换:
(1)极坐标转直角坐标:(2个)
(2)直角坐标转极坐标:(2个)
【参考答案】

22. 什么条件下,平面问题的应力分布与材料的弹性参数无关?
【参考答案】

23. 用量刚分析法设置应力函数:(针对楔形体、半平面体)应力函数的形式:
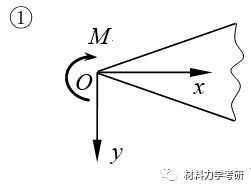
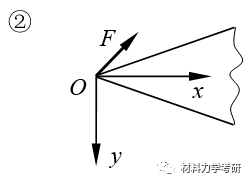
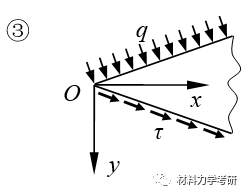
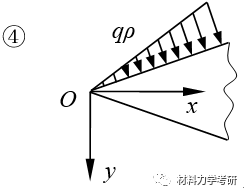
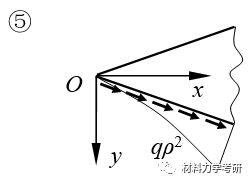
【参考答案】



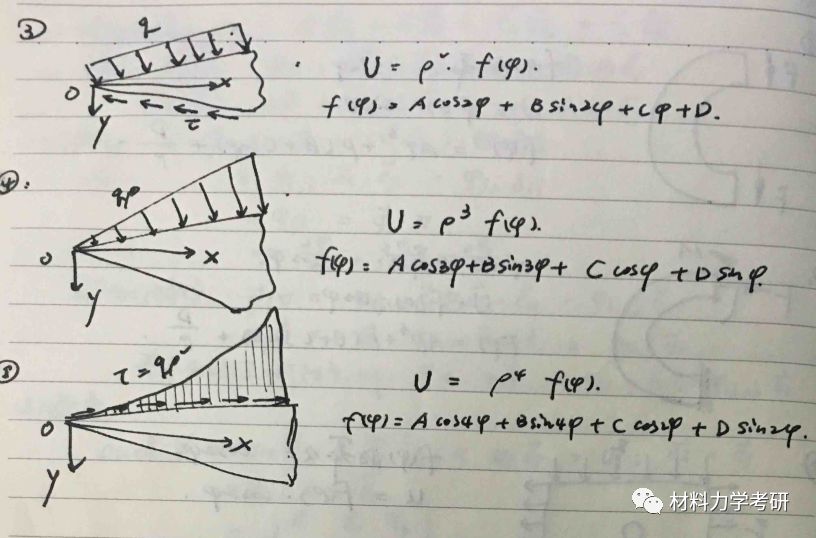
24. 由应力特征导出应力函数:
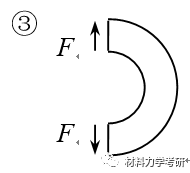
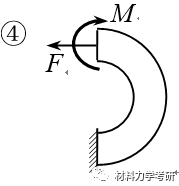
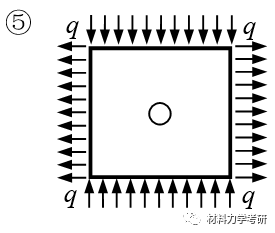
【参考答案】
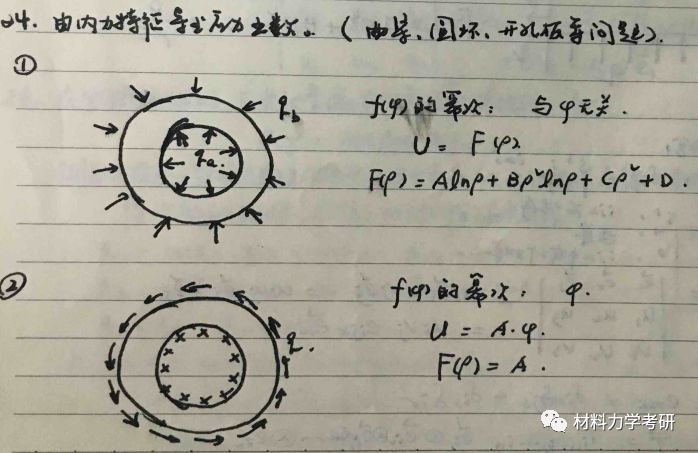
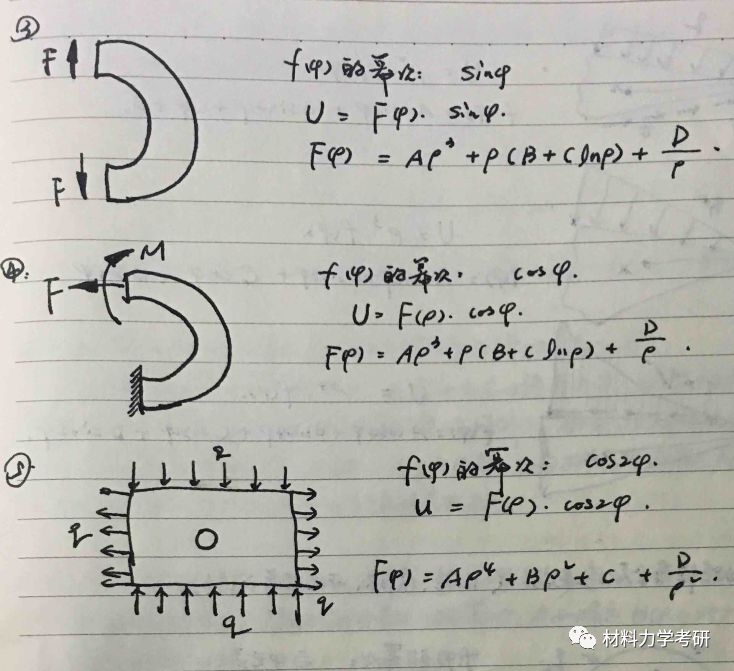
张量基础
25.
哈密顿算子:
梯度:
散度:
旋度:
【参考答案】
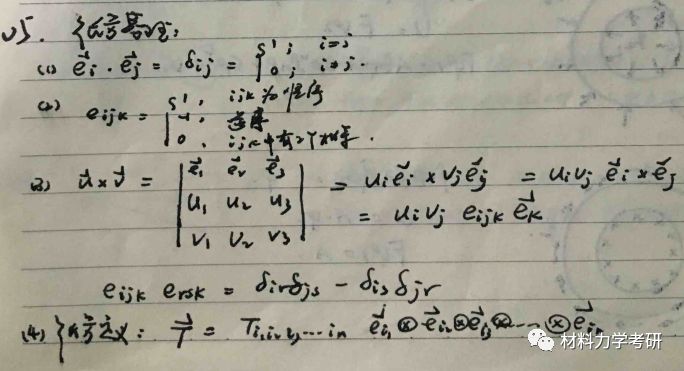
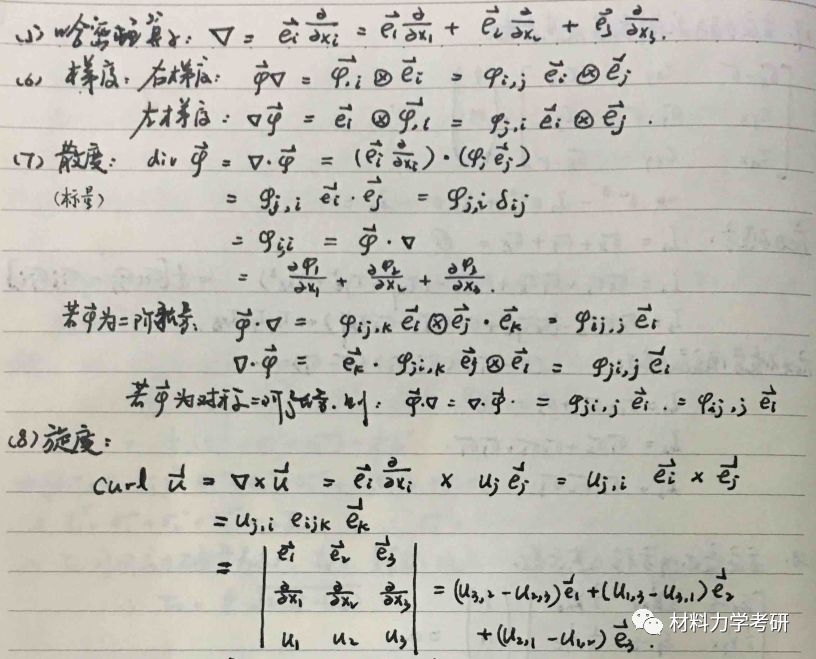
26. 主应力求解方程:(矩阵表示)
系数(3个应力不变量):
应力不变量用主应力表示:(3个)
【参考答案】

27. 主应变求解方程:(矩阵表示)
系数(3个应变不变量):
应变不变量用主应变表示:(3个)
【参考答案】

28. 等截面杆件扭转问题应力函数解法步骤:
1)设置应力函数,满足: ;
2)满足协调方程: ;
3)满足端部条件: ;
4)求出待定系数,确定应力函数;
5)求出切应力: ; ;
6)代入物理方程求切应变: ; ;
7)根据几何方程求出位移: ; 。
【参考答案】

薄板小挠度弯曲问题
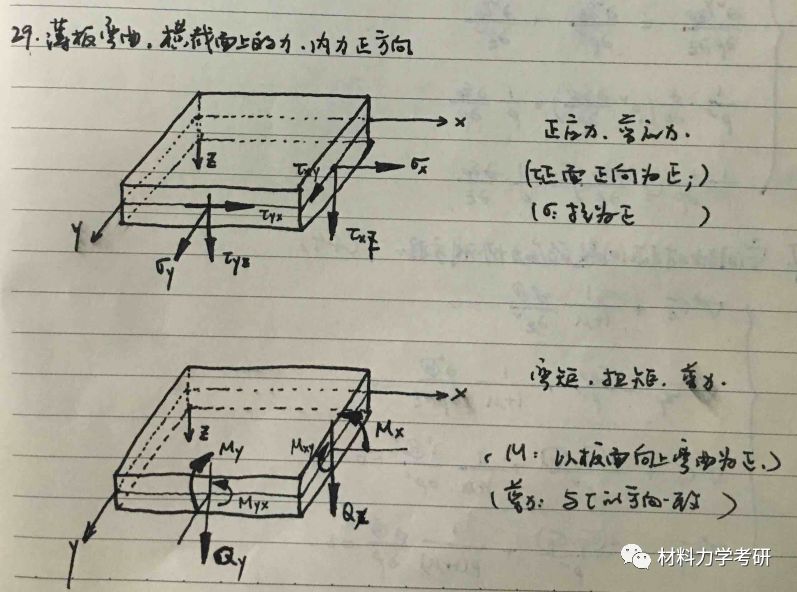
29. 画出横截面上力、内力的正方向:
(1)正应力和切应力:
(2)弯矩、扭矩、剪力、角点反力:
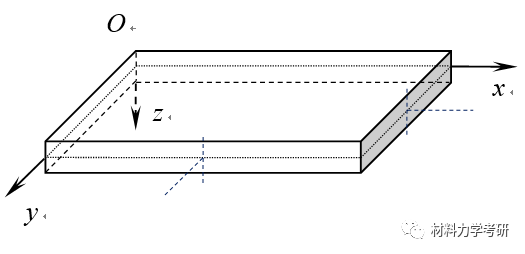
【参考答案】
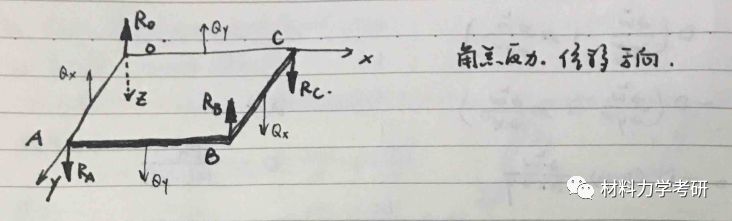
30. 薄板弯曲问题中,基于克希霍夫假设(直法线假设;中面内无x、y向位移;σz引起的应变可忽略),于是:
w= ;
u= ;v= ;
εx= ;εy= ;γxy= ;
γxz= ;γzy= ;εz= ;
31. 用挠度表示的应变和曲率(扭率):
(1)应变分量(3个)
(2)曲率(扭率):(3个)
【30-31参考答案】

32. 用挠度表示的应力(6个)和内力(5个):
(1)主要应力(3个)
(2)次要应力(2个)
(3)更次要应力(1个)
(4)内力(5个):
【参考答案】


33. 应力与内力关系(应力用内力表示):(6个)
34. 不同内力之间的关系:(4个)
【33-34参考答案】
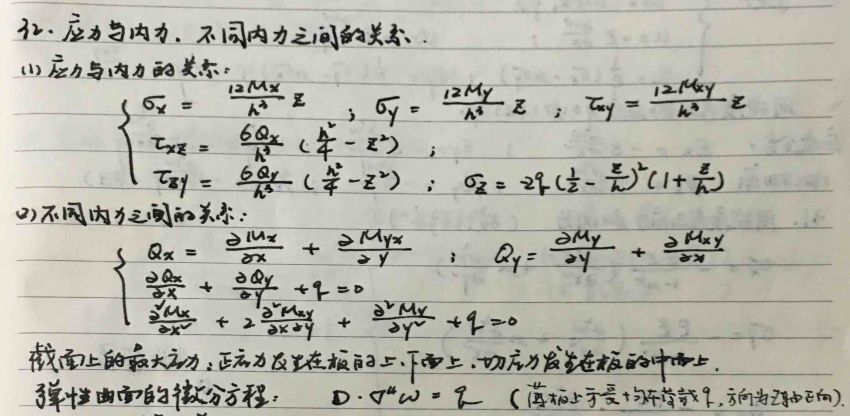
35. (1)弹性曲面的微分方程(直角坐标): ;
(2)扭矩的等效剪力:(2个,直角坐标表示)
(3)角点反力:RB= ;
【参考答案】

36. 矩形薄板的纳维解(Navier):
(1)适用条件: ;
(2)挠度函数:
【参考答案】

37. *矩形薄板的李维解(Lēvy):
(1)适用条件: ;
(2)挠度函数:
【参考答案】

38. 圆形薄板的一般弯曲问题(极坐标)
(1)挠曲面微分方程(极坐标): ;
(2)用挠度表示的内力:(5个)
(3)合剪力:(2个,极坐标表示)
【参考答案】
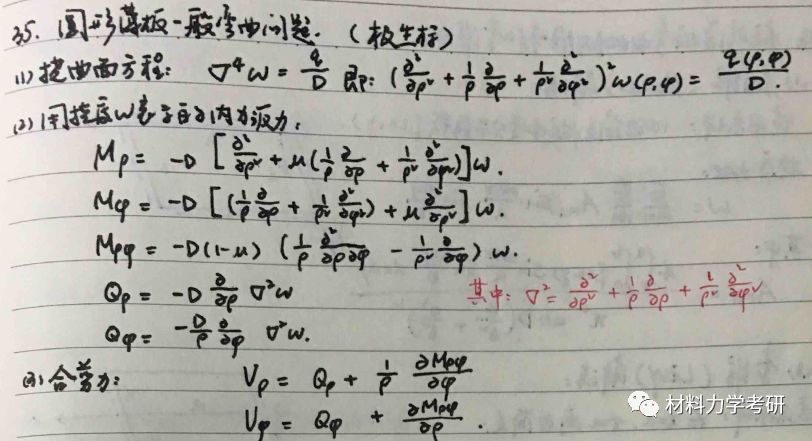
39. 圆形薄板的轴对称弯曲问题(极坐标)
(1)挠曲面微分方程(极坐标): ;
(2)用挠度表示的内力:(5个)
(3)合剪力:(2个,极坐标表示)
【参考答案】

40. 圆形薄板轴对称弯曲时的挠度解:
w= ,
其中,w1 = 。
【参考答案】
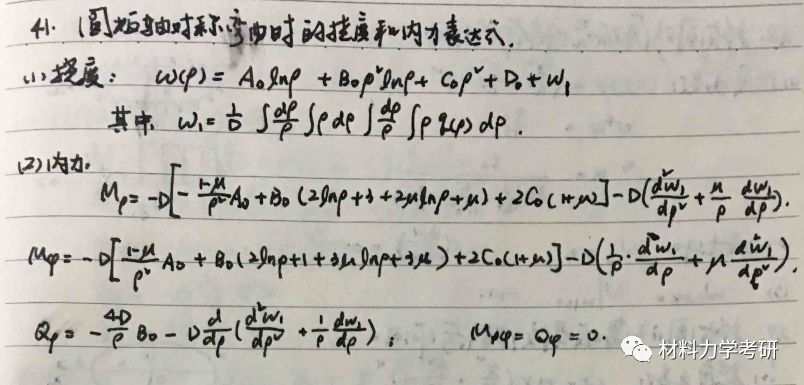
41. 几类弹性力学问题求解方程归纳表
名称 | 坐标系 | 求解方程形式 | 拉普拉斯算子 | 方程实质 | ||
薄板弯曲问题 | 位移解法 | 一般情况 | 直角坐标 | 以位移表示的平衡方程 | ||
极坐标 | ||||||
轴对称 | 极坐标 | |||||
平面问题 | 应力解法 | 一般情况 | 直角坐标 | 以应力函数表示的协调方程 | ||
极坐标 | ||||||
轴对称 | 极坐标 | |||||
空间问题 | 位移解法 | 轴对称 | 柱坐标 | 平衡条件 | ||
球对称 | 球坐标 | 平衡条件 | ||||
应力解法 | 直杆扭曲 | 直角坐标 | 以应力函数表示的协调方程 | |||
梁弯曲 | 直角坐标 | |||||
【略,这里补充空间问题的求解方法参考答案】


弹性力学的变分解法
42. 比能vε(应变能密度):单位体积内的应变能(3种表达形式)
(1)用应力应变表示:
(2)用应力表示:
(3)用应变表示:
43. 应变能密度vε与应变的关系(格林公式):(6个)
【42-43参考答案】

44. 单位体积的余能vc与应变的关系(卡斯蒂利亚诺公式):(6个)
(注:对于线弹性体,由于vε=vc,因此,单位体积的余能vc可以用比能vε代替。)
【参考答案】

45. 位移变分方程、最小势能原理、虚功方程。
(1)位移变分方程:
(2)最小(极小)势能原理:
(3)总势能:
(4)虚功方程:
【略,具体请看第46题】
46. 瑞利-利兹法解题步骤:
(1)求解梁弯曲问题:
a)设定满足梁两端位移约束条件的挠度函数:w(x)=∑Bmvm(x)。
b)计算梁的总势能Ep:
c)由最小势能原理求解系数Bm:
d)得到挠度w(x)=∑Bmvm(x)。
(2)求解平面问题(平面应力):
a)设定满足位移约束条件(u0, v0)的位移函数:u = u0 + ∑Amum;v = v0 + ∑Bmvm。
b)计算应变能Vm:
c)确定待定系数系数Am,Bm:
d)代入物理方程和几何方程,可得到应力分量。
(3)求解矩形薄板弯曲问题:
a)设定满足位移约束条件的挠度函数:w(x, y)=∑Cmwm。
b)计算应变能Vm:
(对于周边固定或简支的情况,应变能Vm = 。)
c)求解系数Cm:
d)得到挠度w(x)=∑Bmvm(x)。
(4)求解圆形薄板弯曲问题:(轴对称弯曲)
a)设定满足位移约束条件的挠度函数:w(ρ) = ∑Cm·wm(ρ)。
b)计算应变能Vm:
c)求解系数Cm:
d)得到挠度w(ρ) = ∑Cm·wm(ρ)。
【参考答案】


获取更多材料力学考研相关资料,请关注微信公众号:材料力学考研、新浪微博:材料力学考研。即日起,“材料力学考研”新浪微博将与“材料力学考研”微信公众号同步发送消息。至此,我们将形成QQ、微博、微信公众号多个平台为大家分享信息!
本公众号服务广大考研学生,搜集整理材料力学考研复习资料及全国各大高校的材料力学考研专业课试题。公众号的特色板块包括:基础练习、强化训练、冲刺拔高等。基础训练板块为大家提供“每日一题”、“知识点梳理”、“课后习题详解”、“视频教程”栏目,主要为基础题;强化训练版快包括“材料力学题库”、“考研真题详解”、“模拟试题”、“周周练(难题)”栏目;冲刺模拟包括“力学竞赛”、“弹性力学”、“土木工程考研复试”等栏目,还有专门针对报考土木工程专业的“复试专栏”。欢迎大家扫码关注: