机器学习(周志华)——第 4 章 决策树
1、决策树学习算法包括哪几个部分?常用的算法有哪些?
决策树是一种基本的分类与回归方法,主要包含了 3 个步骤:特征选择、决策树的生成和决策树的修剪. 常见的决策树算法有:ID3,C4.5,CART.
2、决策树的根节点、内部节点和叶节点分别表示什么?
根节点 —— 一个特征或属性(包含所有测试样本)
内部节点 —— 一个特征或属性(包含部分测试样本)
叶节点 —— 一个类
决策树学习的损失函数通常是正则化的极大似然函数
3、特征选择的准则有哪些(如何选择最优划分属性)?
在属性划分的过程中,我们希望决策树的分支节点所包含的样本尽可能属于同一类别,即节点的 “纯度” 越来越高,这样就可以减少划分次数,节约计算资源.
**主要的准则有:**信息增益(information gain)、增益率(gain ratio)、基尼指数(gini)
(1) 信息增益
介绍信息增益前,需要对 “信息熵” 进行解释.
信息熵是度量样本集合纯度最常用的一种指标,信息熵越小,说明样本集合纯度越高. 假设当前集合 D DD 中第 k kk 类样本所占的比例为 p k p_{k}pk(k kk = 1,2,…,|y yy|),则 D DD 的信息熵定义为:
E n t ( D ) = − ∑ k = 1 ∣ y ∣ p k l o g 2 p k Ent(D) = -\sum_{k=1}^{|y|}p_{k}log_{2}p_{k}Ent(D)=−k=1∑∣y∣pklog2pk
假定对西瓜的离散属性 “敲声”(用 a 表示) 有 3 (用 v 表示,v=1,2,3) 个可能的取值 {浊响,沉闷,清脆},若使用 “敲声” 来对样本集 D DD 进行划分,则会产生 3 个分支结点,其中第 1 个分支结点包含了 D DD 中所有在 “敲声” 这一属性上取值为 “浊响” 的样本,记为 D 1 D^{1}D1. 我们可根据下式计算出 D 1 D^{1}D1 的信息熵,再考虑到不同的分支结点所包含的样本数不同,给分支结点赋予权重 |D v D^{v}Dv| / |D DD|,即样本数越多的分支结点的影响越大,于是可计算出用属性 “敲声” 对样本集D进行划分所获得的“信息增益”(information gain).
G a i n ( D , a ) = E n t ( D ) − ∑ k = 1 ∣ y ∣ ∣ D v ∣ ∣ D ∣ E n t ( D v ) Gain(D,a) = Ent(D)-\sum_{k=1}^{|y|} \frac {|D^{v}|}{|D|}Ent(D^{v})Gain(D,a)=Ent(D)−k=1∑∣y∣∣D∣∣Dv∣Ent(Dv)
一般而言,信息增益越大,则意味着使用属性a来进行划分所获得的 “纯度提升” 越大. 如上式,前一部分为当前样本集合 D DD 的信息熵,为一个确定数 E n t ( D ) Ent(D)Ent(D) ,后一部分表示以某个属性进行划分,划分后的信息熵,若后部分的信息熵很小,则表示用该属性进行划分 “纯度提升” 很大. 由此可确定当前节点的划分属性.
(2) 增益率
由于信息增益准则对可取值数目较多的属性有所偏好,为减少这种偏好带来的不利影响,C 4.5 C4.5C4.5 决策树算法不直接使用信息增益,而是使用 “增益率” 来选择最优划分属性.
G a i n r a t i o ( D , a ) = G a i n ( D , a ) I V ( a ) Gain_ratio(D,a) = \frac {Gain(D,a)}{IV(a)}Gainratio(D,a)=IV(a)Gain(D,a)
其中
I V ( a ) = − ∑ v = 1 V ∣ D v ∣ ∣ D ∣ l o g 2 ∣ D v ∣ ∣ D ∣ IV(a) = -\sum_{v=1}^{V} \frac{|D^{v}|}{|D|}log_{2} \frac{|D^{v}|}{|D|}IV(a)=−v=1∑V∣D∣∣Dv∣log2∣D∣∣Dv∣
称为属性 a aa 的 “固有值” —— 熵 . 属性 a aa 的可能取值数目越多 (即V VV 越大),则 I V ( a ) IV(a)IV(a) 的取值通常会越大,那么增益率通常就越小.
需要注意的是, 增益率准则对可取值数目较少的属性有所偏好,因此,C 4.5 C4.5C4.5 算法并不在直接选择增益率最大的候选划分属性,而是使用了一个启发式:先从候选划分属性中找出信息增益高于平均水平的属性,再从中选择增益率最高的.
(3) 基尼指数
C A R T CARTCART 决策树是使用 “基尼指数” 来选择划分属性. 数据集 D DD 的纯度可用基尼值来度量.
G i n i ( D ) = ∑ k = 1 ∣ y ∣ ∑ k ′ ≠ k p k p k ′ = ∑ k = 1 ∣ y ∣ p k ( 1 − p k ) = 1 − ∑ k = 1 ∣ y ∣ p k 2 Gini(D) = \sum_{k=1}^{|y|} \sum_{k' \neq k}p_{k}p_{k'} = \sum_{k=1}^{|y|} p_{k}(1-p_{k})= 1- \sum_{k=1}^{|y|} p_{k}^{2}Gini(D)=k=1∑∣y∣k′=k∑pkpk′=k=1∑∣y∣pk(1−pk)=1−k=1∑∣y∣pk2
G i n i ( D ) Gini(D)Gini(D) 反映了从数据集 D DD 中随机抽取两个样本,其类别标记不一致的概率. 因此,G i n i ( D ) Gini(D)Gini(D) 越小,样本不一致的概率越小,则数据集 D DD 的纯度越高.
G i n i _ i n d e x ( D , a ) = ∑ k = 1 ∣ y ∣ ∣ D v ∣ ∣ D ∣ G i n i ( D v ) Gini\_index(D,a) = \sum_{k=1}^{|y|}\frac{|D^{v}|}{|D|}Gini(D^{v})Gini_index(D,a)=k=1∑∣y∣∣D∣∣Dv∣Gini(Dv)
4、 决策树如何防止过拟合?
预剪枝
预剪枝是要对划分前后泛化性能进行评估,对比决策树某节点生成前与生成后的泛化性能。若当前节点的划分不能带来决策树泛化性能提升,则停止划分并将当前节点标记为叶节点。

假设我们将这个叶节点标记为 “好瓜” ,在用属性 “脐部” 划分前,从验证集中可以看出,编号{4, 5, 8}被分类正确,正确率 3/7 . 若以属性 “脐部” 进行划分,训练集中 {1, 2, 3, 14}——好瓜,{6, 7, 15, 17}——好瓜,{10, 16}——坏瓜,验证集中有 {4, 5, 8, 11, 12} 分类准确,精度为 5/7 . 预剪枝的决策是划分. 其他属性的划分如下图所示.
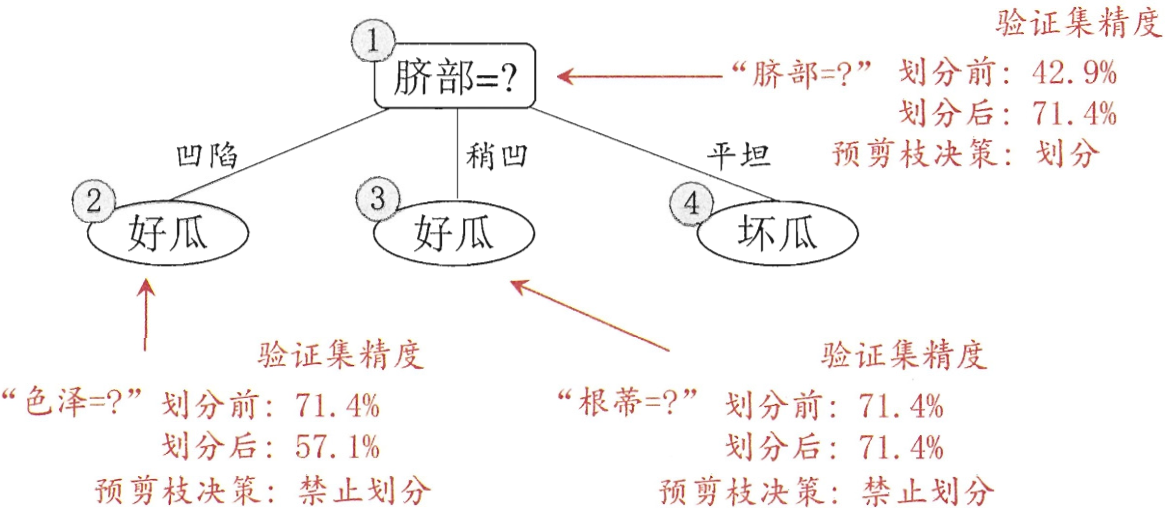
后剪枝
后剪枝表示先从训练集中生成一颗完整决策树,子弟向上地对非叶节点进行考察,若将该节点对应的子树替换成叶节点能提升泛化性能,则将该子树替换成叶节点。
从图 4.1 中首先可考虑对属性 “纹理” 进行剪枝,剪枝后有编号为{7, 15}的样本,若对其进行剪枝,叶节点标记为好瓜,
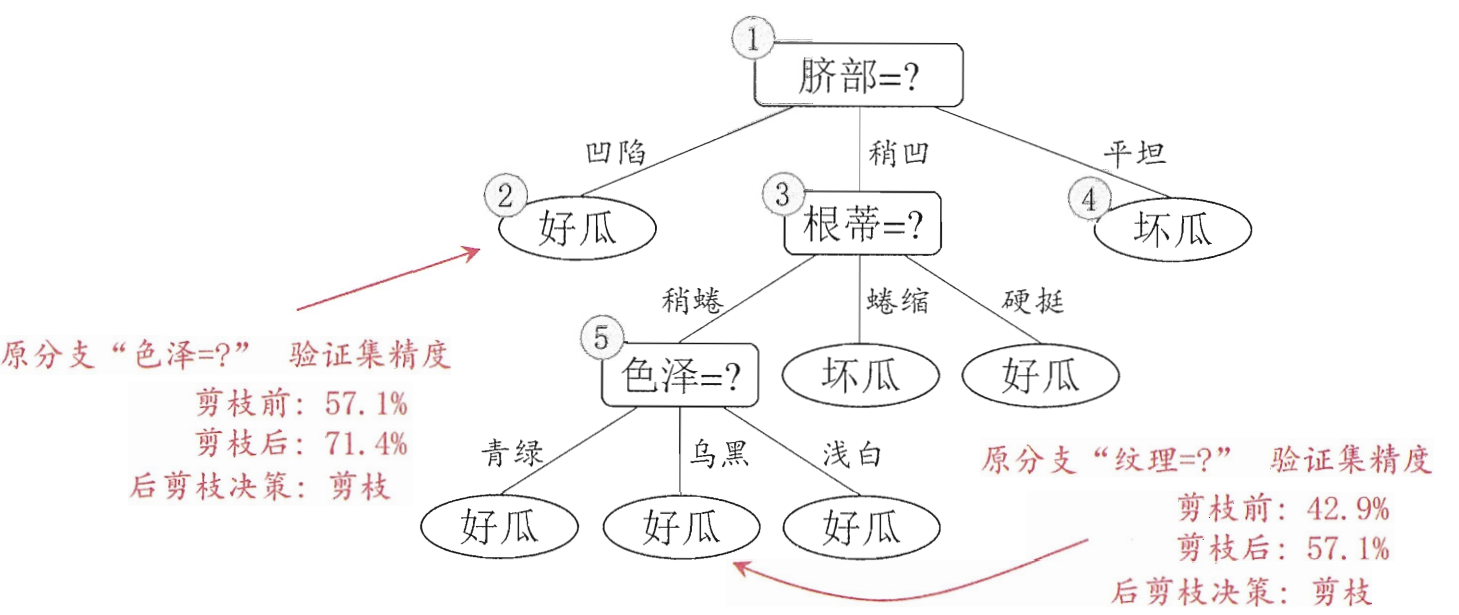
5、对 ID3,C4.5 以及 CART 的区别进行小结
ID3:划分选择依据是信息增益,缺点是信息增益准则对可取数目较多的属性有偏好。
C4.5:划分选择依据是信息增益率,与 ID3 不同,其对可取数目较少的属性有偏好,可取数目是指一个属性下的可能取值,如 “色泽” = {青绿,乌黑,浅白},则可取数目是 3,改进版本是先找到信息增益高于平均水平的属性,再从中选出信息增益率最高的属性。
CART:划分选择依据是基尼指数。