数据结构与算法基础

1.数组与矩阵

数组

首字母+偏移量：有(2*5+3) *2+a

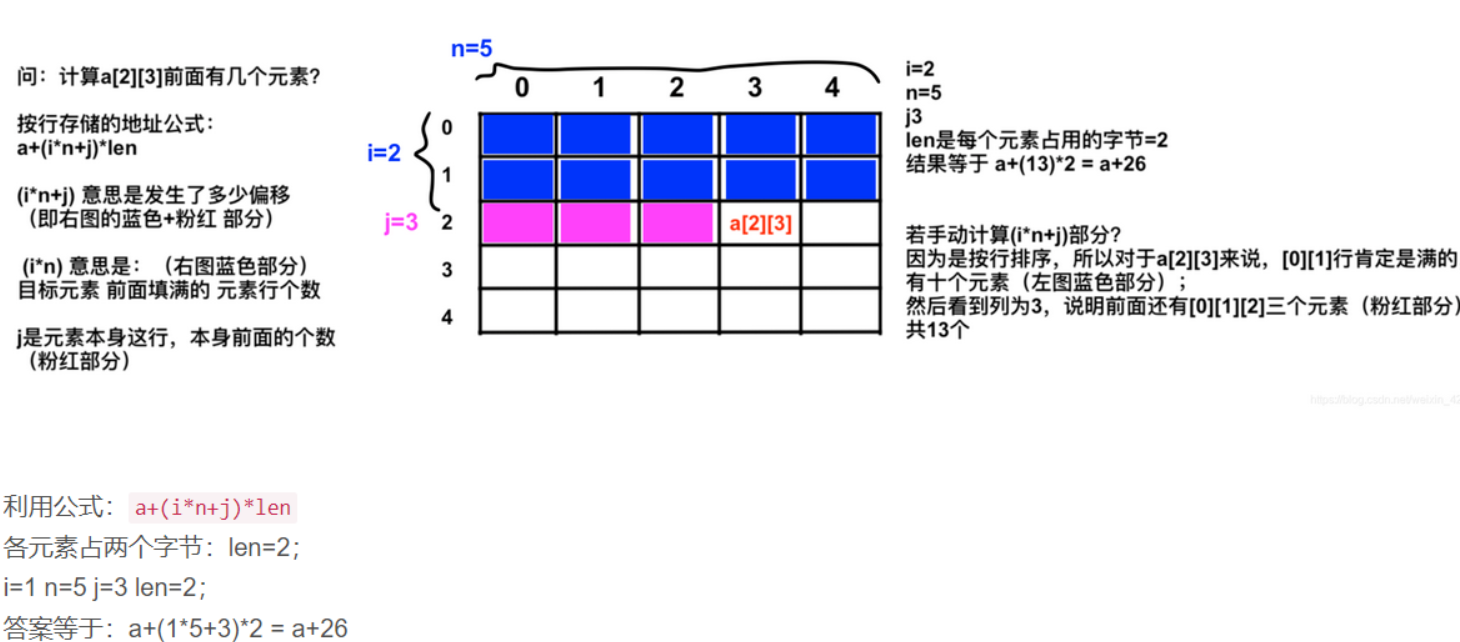
稀疏矩阵 _代入计算

解题思路：代入排除法

2.线性表***

线性表是N个具有相同特性的数据元素的有限序列

2.1顺序表

数组，地址上连续的存储单元，数组可静态分配或动态扩展；

优点：随机访问特性，查找O(1)时间，存储密度高，逻辑物理均相邻

缺点：插入删除操作需要移动大量元素

2.2链表

递归，为空或者指向另一个结点的node引用，该节点含有下一个结点或链表的引用；存储空间可不连续，插入删除不需要移动大量元素，但查找某个结点时需要从头遍历

2.2.1类型

单链表：头结点依次指向尾结点

循环链表：

双向链表：

2.2.2操作

单链表：删除结点、插入结点

双向链表：删除结点、插入结点

顺序存储和链式存储二者比较

查找操作中时间复杂度一致；读运算顺序更优

2.3队列和栈

队列：先进先出、两端都可操作

栈：先进后出、一端操作

3.广义表

是由n个表元素组成的有限序列，是线性表的推广

长度：最外层表包含元素的个数–如图长度为三(例一)

深度：包含括号的重数–a一重，b一重共两重

表头：最外层的元素；表尾：除了表头的元素(例二)

​

4.树与二叉树***

• 结点的度：一个结点所拥有的的孩子结点数

• 

• 树的度：结点度最多的那个1\2

• 叶子结点：无孩子结点的如7\8

• 分支结点：根节点以下

• 内部结点：根节点和叶子结点之间的

• 父节点:2是4的父节点

• 子结点：4是2的子结点

• 兄弟结点：4和5是兄弟结点

• 层次：分层

经过前人的总结，二叉树具有以下几个性质：
    1.二叉树中，第 i 层最多有 2i-1 个结点。
    2.如果二叉树的深度为 K，那么此二叉树最多有 2K-1 个结点。
    3.二叉树中，终端结点数（叶子结点数）为 n0，度为 2 的结点数为 n2，则 n0=n2+1。
    4.如果对一颗有n个结点的完全二叉树的结点按层序号编号(从第一层多(log2n)+1层，每层从左到右)，则对任意结点有(1<=i<=n):
    如果i=1,则结点无父节点，是二叉树的根；如果i>1，则父节点是i/2
    如果2i>n,则结点i为叶子结点，无左子节点；否则其左子节点是2i
    如果2i+1>n,则结点i无右子结点，否则，其右子结点是2i+1

4.1满二叉树和完全二叉树

满二叉树：每个结点的度都为2

完全二叉树：除去最后一层结点为满二叉树，且最后一层的结点依次从左到右分布

4.2二叉树的遍历

1. 前序遍历：根左右(当前)
2. 中序遍历：左根右
3. 后续遍历：左右根–当前左右子树遍历完之后遍历该结点
4. 层次遍历：第一层从左到右

前、中、后续和层次遍历依次为：

1 2 4 5 3 6 7

4 2 5 1 6 3 7

4 5 2 6 7 3 1

1 2 3 4 5 6 7

4.3树转二叉树

①：当前孩子结点作为左子树的结点，当前层的兄弟结点作为左子树的右孩子结点

②：兄弟结点连接，多个孩子只保留第一个，旋转置换获得

4.4查找(排序)二叉树

左孩子<根<右孩子

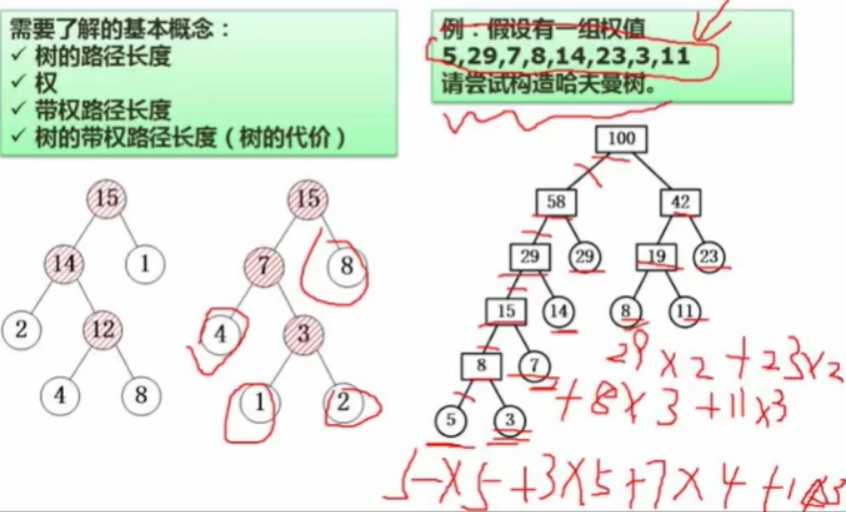
4.5最优(哈夫曼)二叉树

是一种无损压缩方式

树的路径长度：路径相加的和

权：叶子结点出现的频度

带权的路径长度：路径长度*权值

树的带权路径长度：各路径长度的和，最优要求路径最短

4.6线索二叉树

很多结点是空的，将空闲资源利用起来从而构成线索二叉树

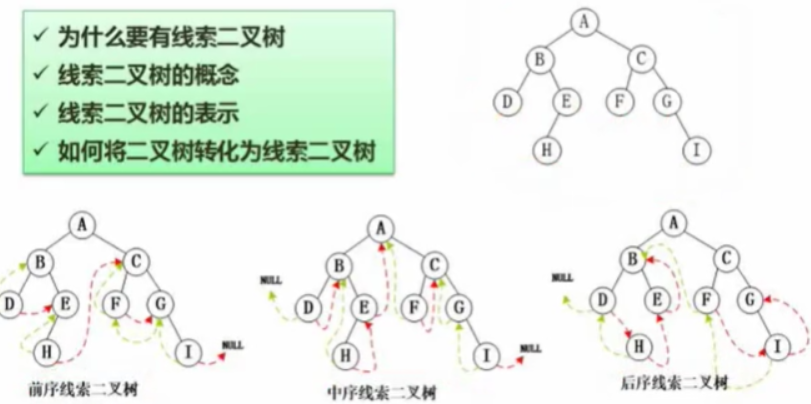
根左右ABDEHCFGI—左根右DBHEAFCGI—左右根DEHBFGICA

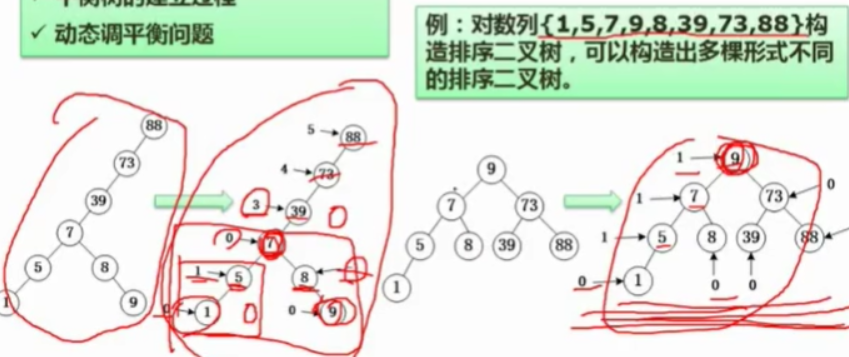
4.7平衡二叉树

提出原因？

定义：任意结点的左右子树深度相差不超过1；每个结点的平衡度只能为-1,0或1===>平衡度：叶子结点：0，左子树减右子树的情况：左0右1为负一，左1右0为一

建立过程？动态平衡？

5.图

5.1基本概念

5.2存储方式

5.2.1邻接矩阵

1到1没有连线则用0表示，1到2有连线则为1

无向图具有对称性，可以存储上或下三角矩阵信息节省空间

5.2.2邻接表

V1–>[指向的下一结点，距离]

5.3图的遍历

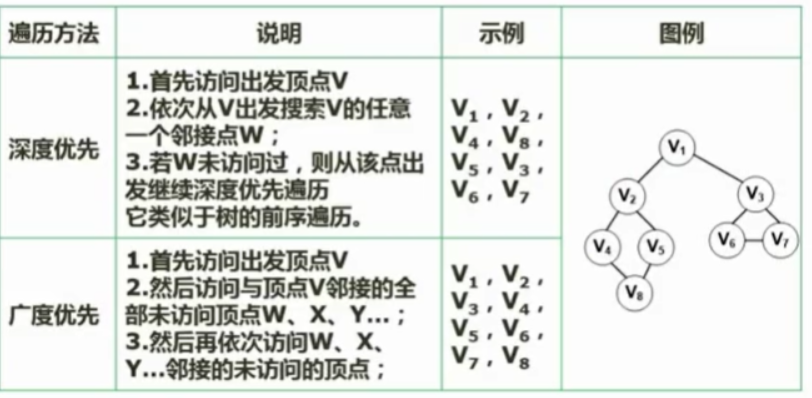
5.3.1深度优先遍历

遍历完左子树后再遍历右子树(根左右)；纵向;都被访问过则逐层往上回退，直到找到未访问过的再依次按照未访问的邻接点遍历

5.3.1广度优先遍历

一层一层一次遍历(层次遍历)；横向

考察方式：给出领接矩阵\邻接表求深度广度优先

5.4拓扑排序

用有向边表示活动之间开始的先后关系；这种有向图称为用顶点表示的活动网络(AOV网络)

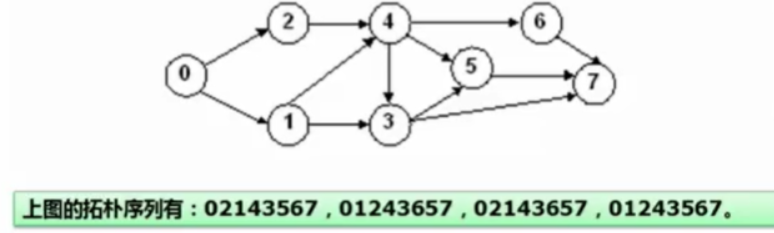
关键路径的几个重要概念：

顶点j事件的最早发生时间：从源点到j的最长路径Ve(j)

顶点j事件的最迟发生时间：不推迟完成时间的前提下，一个事件j允许最迟的发生时间Vl(j)

正推求最大，反推求最小

5.5图的最小生成树

将图的线和边去掉，所有权值相加最小

树和图最大的区别：树没有环路而图有，树的结点为n时边最多为n-1,图的结点和边相等

首先确定最小生成树的长度：为图的边-1，即线条数

从根节点无法到达的节点用∞表示

普里姆算法：从一个任意结点出发，下一红点集出发连接最小边，形成树

克鲁斯卡尔算法:先确定边，避免成环，继续选择最小边，直到边的数目达到要求

6.排序与查找***

6.1排序的概念

• 稳定与不稳定排序

稳定：键值顺序不会因为排序而改变；

不稳定：相等的数在排序之后的顺序改变了

• 内排序和外排序

内排序：在内存(随机存储器)中的排序

外排序：排序的数量级很大，内存装不下，需要用外存进行访问的排序

6.2排序分类

6.2.1插入类排序

• 直接插入排序

将要插入的元素放入已经排序好的序列中，从大到小或从小到大依次比较放入合适的位置中，速度很慢；第一个数必然有序，将无序的数与有序数依次比较；n个数要便利n-1次

• 希尔排序

先按固定间隔分组(总长度的一半)，组内插入排序，再减小组内间隔再插入排序；分成n组，组内间隔则为n

二者区别：插入排序的比较次数都比希尔排序的多得多，效率自然低

6.2.2交替类排序

• 冒泡排序

外层n次循环，内层n-1次循环，每次循环只拿一个元素与其他元素比较

• 快速排序

使用分治法排序，递归，是二分法的一种优化；分治不存在强调当前步骤和整体最优一说法

6.2.3选择类排序

• 直接选择排序

每次选择最小的元素

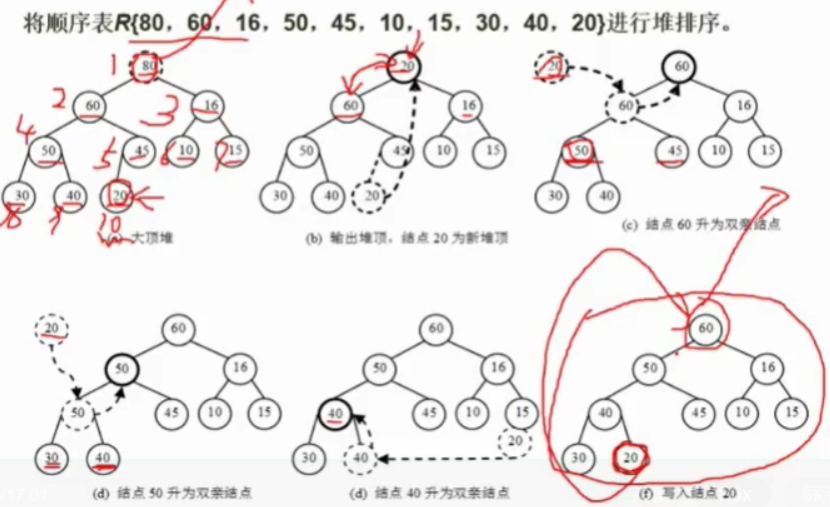
• 堆排序

是所有排序算法中最复杂的一种

当子结点**>根节点时为小顶堆，当子结点<根节点时为大**顶堆；根小堆小，根大堆大；相当于完全二叉树

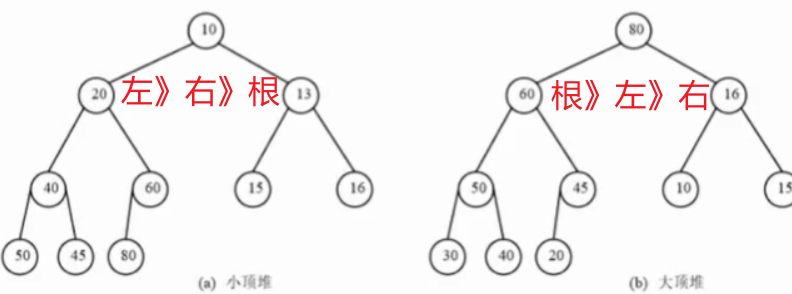
堆的思想：先建立堆，输出堆顶元素，取走之后均为剩余里面最小的元素

先用完全二叉树排序数组元素，再依次根据堆顶规则调整

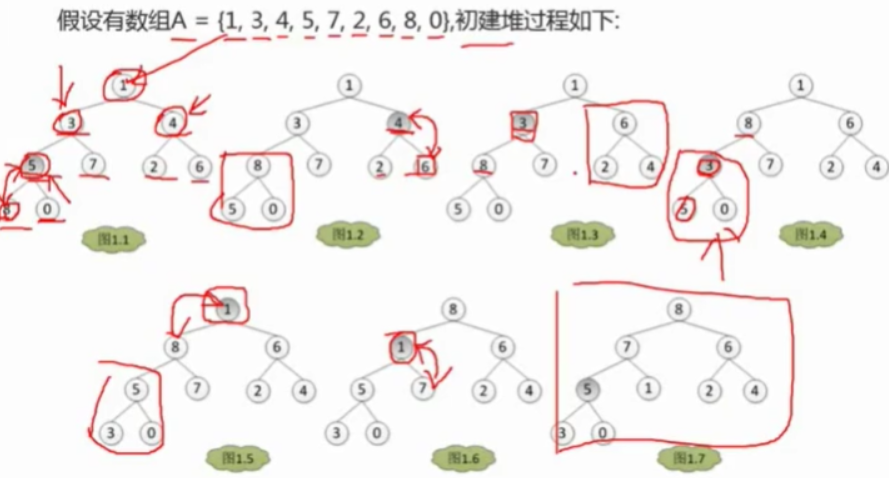
堆排序实现：把顶结点取出—将最后的结点放到顶部–再将其依次与子结点进行比较—直到得到新一轮完全二叉树…再去顶重复操作

6.2.4归并排序

将两个或两个以上的有序表和并成一个新的有序表

6.2.5基数排序

非重点

7.算法基础及常见算法***

7.1算法的特性

• 有穷性：执行有穷步后结束
• 确定性：算法中的每一天指令都必须有确切的含义，不能含糊不清
• 输入>=0
• 输出>=1
• 有效性：每个步骤都能有效执行并能得到确定的结果

7.2时间复杂度和空间复杂度

时间复杂度：衡量算法执行所耗费的时间

时间度量:O(1)<O(log₂n)<O(n)<O(nlog₂n)<O(n²)<O(n³)<O(2^n)

树的处理中常用log₂n

空间复杂度：执行过程中要临时占用存储空间大小的度量，只考虑在运算过程中为局部变量分配的存储空间的大小

7.3顺序查找

思想：将待查找的关键字为key的元素从头到尾与表中元素进行比较，如果中间存在关键字为key的元素，则返回成功，否则失败

顺序查找的时间复杂度为O(n),效率并不高;查找的平均次数为(n+1)/2

7.4二分查找

前提：有序排列的(小到大或大到小)

二分查找的中间值为**(head+tail)/2**，非整数时向下取整

时间复杂度为O(log₂n),查找的次数最多为[log₂n]+1

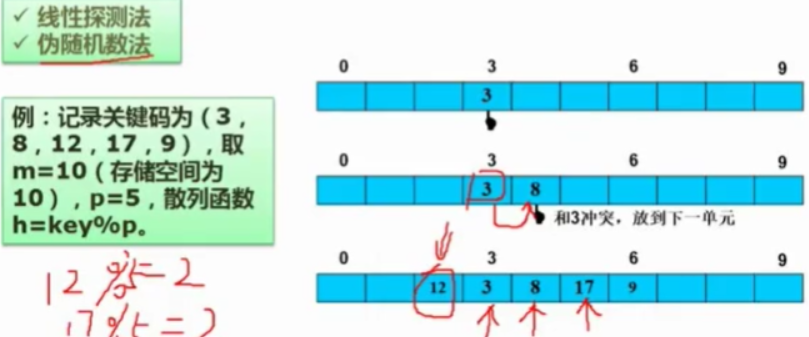
7.5散列表

相当于按类容存储

思想：已知关键字集合U，最大关键字为m，设计一个函数Hash，它以关键字为变量，关键字的存储地址为因变量，将关键字映射到一个有限、地址连续的区间T0…n-1,这个区间就称为散列表，转换函数称为散列函数

key的元素从头到尾与表中元素进行比较，如果中间存在关键字为key的元素，则返回成功，否则失败

[外链图片转存中…(img-hkHAZKj9-1652976233182)]

顺序查找的时间复杂度为O(n),效率并不高;查找的平均次数为(n+1)/2

7.4二分查找

前提：有序排列的(小到大或大到小)

二分查找的中间值为**(head+tail)/2**，非整数时向下取整

时间复杂度为O(log₂n),查找的次数最多为[log₂n]+1

7.5散列表

相当于按类容存储

思想：已知关键字集合U，最大关键字为m，设计一个函数Hash，它以关键字为变量，关键字的存储地址为因变量，将关键字映射到一个有限、地址连续的区间T0…n-1,这个区间就称为散列表，转换函数称为散列函数

[外链图片转存中…(img-xqFQVhg3-1652976233183)]