Exploiting Edge Features in Graph Neural Networks(CVPR 2019)阅读笔记
作者认为 传统GNN例如GAT和GCN都没有很好利用边的特征。在GAT中,当两个节点没有连接的时候,强行让它们的attention为0,然后将图的拓扑信息注入模型。所以,GAT中边的信息只能表示有没有边,也就是连接性。GCN的边可以利用一维的真值边的特征,例如边的权重,但是边的特征被限制为一维的。GAT和GCN的另外一个问题是,各层都使用最开始输入的邻接矩阵,一直不变。
这篇文章的模型建设不同的公式来利用多维度的边的特征。该模型通过让一维特征在网络层之间adpte,也可以使得利用一维特征更有效。该模型还通过use ordinary row or
symmetric edge normalization方法,利用了doubly stochastic normalization来增强GCN和GAT模型。doubly stochastic matrics在利用边上,有很好的性能。
EGNN和传统的GNN比较:
- 邻接矩阵。
传统GNN的邻接矩阵就是a binary matrix(0或者1),表示各个点的邻居关系,GAT也是这样。在GCN中,邻接矩阵是一个都是正值的矩阵,每个值都是一维的边的特征。
而EGNN的邻接矩阵是多维的正值矩阵。(矩阵中每个值都有多个维度,来表示每条边的多个属性) - 邻接矩阵的喂法
传统GNN每一层都输入相同的邻接矩阵A,而EGNN中,在输入到下一层之前,每一层的边的特征都在改变。
节点 X = NF
边 F = NNP
l层数
输入 X0和E0,过了一层,X0变成X1 = NF1,E0变成E1(维度不变)。
The node features XL can be considered as an embedding of the graph nodes in an FL-dimensional space.
对于节点分类问题,沿着最后一个维度,每个节点embedding vector XiL都应用一个softmax operator。
对于整个图的预测(分类或者回归),在XL的第一个维度应用一个池化层pooling layer使得特征矩阵简化为一个整个图的单个vector embedding。然后一个全连接层应用于该向量上,全连接层的输出可以被用来做回归的预测,或者是分类。
EGNN的输入E0是已经被预归一化了,归一化的方法:
两种类型的EGNN层,基于attention的EGNN(EGNN(A))layer和基于convolution的EGNN(EGNN©) layer
图卷积的操作,边特征矩阵当成filter用来和节点特征矩阵相乘,为了避免由于乘法导致的输出特征维度增加,边特征需要被归一化。
这个doubly stochastic normalization看不懂为什么要这样:

表明,边的维度上,每一个维度都是一个正方形矩阵,所有的行或者列的和都是1
往下看不懂了(双随机矩阵)。
GAT的归一化: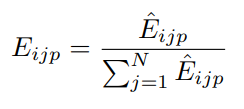
GCN的归一化:
这么做优点在于,因为在多层图申精网络中,边缘特征矩阵会在不同的层之间重复相乘,因此采用双随机归一化可以使得过程更加稳定。
版权声明:本文为SUNNYMOOD1995原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。