线性规划模型与求解
1.线性规划定义
1.1.线性规划模型
我们用不等式和单纯形法中顶点坐标的计算方法,给出线性规划模型的两种表示形式:不等式形式和等式形式
1.2.线性规划问题的解的概念
可行解:满足约束条件的解。
可行域:可行解构成的集合。
最优解:使目标函数达到最大(最小)值的解。
2.求解线性规划的matlab解法
2.1.基于matlab求解器的解法
首先应将问题化为标准模型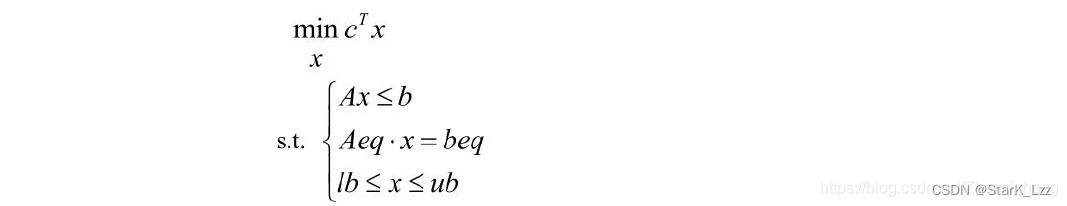 其中c和x为n维列向量,A、Aeq为适当维数的矩阵,b、beq为适当维数的列向量。【注意:matlab是求的是最小值,不等式的不等号是≤ \le≤】
其中c和x为n维列向量,A、Aeq为适当维数的矩阵,b、beq为适当维数的列向量。【注意:matlab是求的是最小值,不等式的不等号是≤ \le≤】
用linprog命令求解线性规划问题 x返回值是决策向量取值,fval返回值是目标函数最优值 【命令中的空项目用[ ]代替即可】
[x,fval] = linprog(c,A,b)
[x,fval] = linprog(c,A,b,Aeq,beq)
[x,fval] = linprog(c,A,b,Aeq,beq,lb,ub)
2.2.基于问题的解法
当约束条件和目标函数比较复杂,运用求和符号或者连乘符号表示,或者决策向量是二维极其以上,用基于问题的解法比较简单。
以下题为例: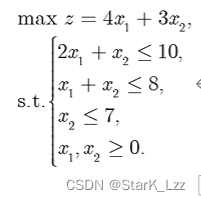
解得最优解为x 1 = 2 , x 2 = 6 x_1=2,x_2=6x1=2,x2=6
目标函数最优值为26
求解matlab程序如下:
clc,clear
probl=optimproblem("ObjectiveSense","max");
%创建最大化线性规划问题(我们的问题是使目标函数值最大,所以要输"ObjectiveSense")
c=[4,3]; %目标函数系数向量
a=[2,1;1,1;0,1];
b=[10;8;7];
x=optimvar("x",2,1,"LowerBound",0);
%定义问题的符号决策向量
%x=optimvar(,行数,列数,,)
probl.Objective=c*x; %问题的目标函数
probl.Constraints=a*x<=b; %问题的约束条件
%如果约束条件有多类,可以再加个标签probl.Constraints.c1,这里只有一类约束条件,所以没有加
[sol,fval,flag,out]=solve(probl)
%一般的线性规划只需要[sol,fval]=solve(probl)
%其中fval是返回的最优值
sol.x %显示决策变量的取值
应用举例:
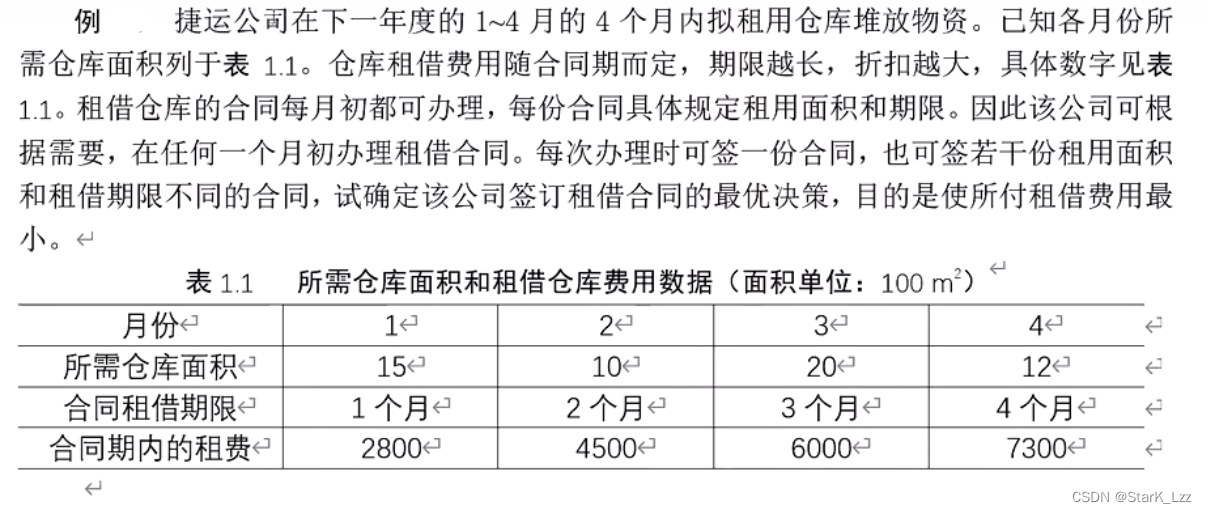 设x i j x_{ij}xij为第i个月份租借期限为j的仓库面积,因为5月份不租仓库,所以x 24 , x 33 , x 34 , x 42 , x 43 , x 44 = 0 x_{24},x_{33},x_{34},x_{42},x_{43},x_{44}=0x24,x33,x34,x42,x43,x44=0,可建立如下模型:
设x i j x_{ij}xij为第i个月份租借期限为j的仓库面积,因为5月份不租仓库,所以x 24 , x 33 , x 34 , x 42 , x 43 , x 44 = 0 x_{24},x_{33},x_{34},x_{42},x_{43},x_{44}=0x24,x33,x34,x42,x43,x44=0,可建立如下模型:
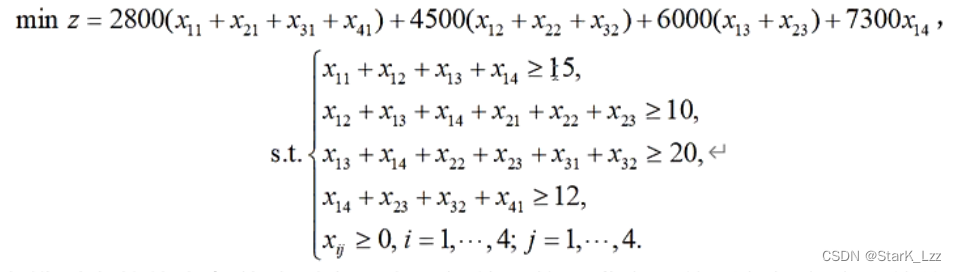 解得最优解为:x 11 = 3 , x 14 = 12 , x 31 = 8 x_{11}=3,x_{14}=12,x_{31}=8x11=3,x14=12,x31=8
解得最优解为:x 11 = 3 , x 14 = 12 , x 31 = 8 x_{11}=3,x_{14}=12,x_{31}=8x11=3,x14=12,x31=8
目标函数最优值是 118400
matlab程序如下:
clc,clear
prob=optimproblem;
x=optimvar("x",4,4,'LowerBound',0);
prob.Objective=2800*sum(x(:,1))+4500*sum(x(1:3,2))+6000*sum(x(1:2,3))+7300*x(1,4);
prob.Constraints=[sum(x(1,:))>=15
sum(x(1,2:4))+sum(x(2,1:3))>=10
sum(x(1,3:4))+sum(x(2,2:3))+sum(x(3,1:2))>=20
x(1,4)+x(2,3)+x(3,2)+x(4,1)>=12];
[sol,fval,flag,out]=solve(prob)
sol.x
3. 运输问题(产销平衡)
运输问题也是线性规划问题,其模型如下 可以用线性规划的解法解决,
可以用线性规划的解法解决,
应用举例
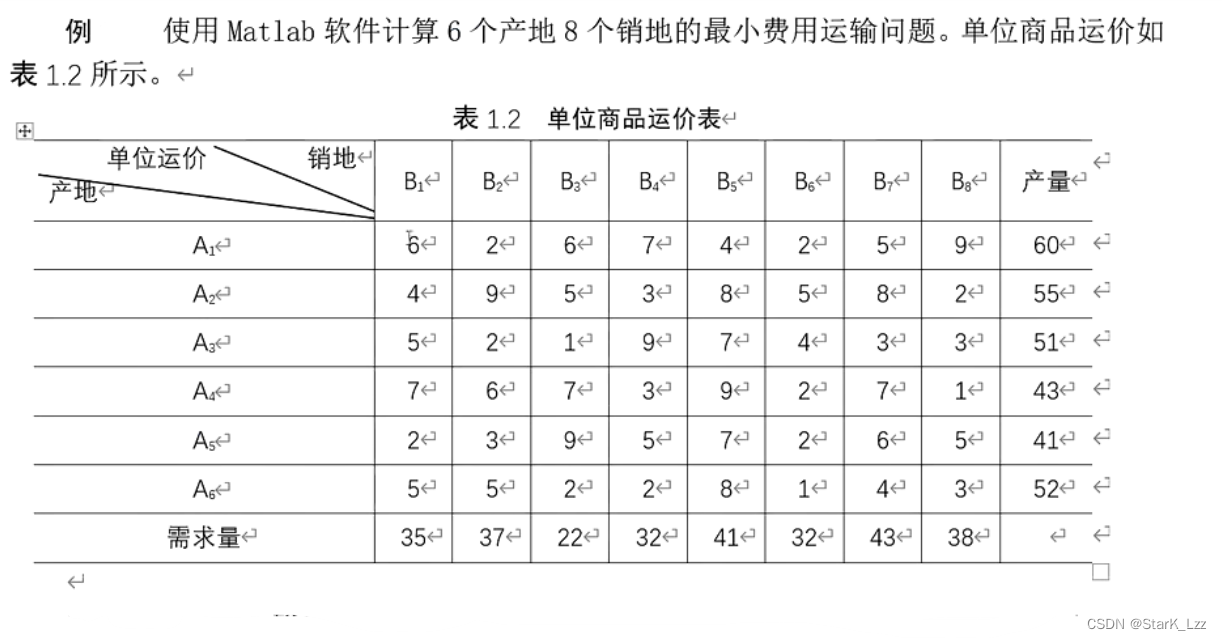 设x i j x_{ij}xij表示从产地A i A_iAi运到到销售地B j B_jBj的量,c i j c_{ij}cij表示产地A i A_iAi运到到销售地B j B_jBj的运价,d i j d_{ij}dij表示销售地B j B_{j}Bj的需求量,c i c_{i}ci表示产地的产量。
设x i j x_{ij}xij表示从产地A i A_iAi运到到销售地B j B_jBj的量,c i j c_{ij}cij表示产地A i A_iAi运到到销售地B j B_jBj的运价,d i j d_{ij}dij表示销售地B j B_{j}Bj的需求量,c i c_{i}ci表示产地的产量。
则目标函数就是使总的运费最小,约束条件有,销售地需求量等于运送量;运送量小于等于产地产量。
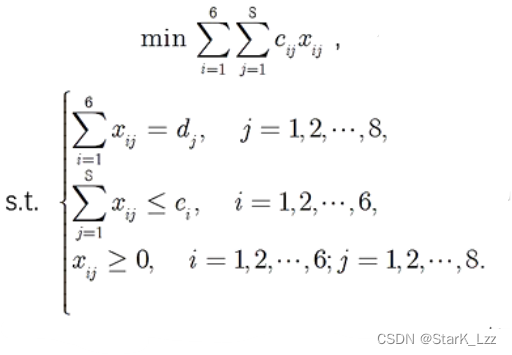
我们用基于问题的方法求解这个线性规划,得到x 12 = 19 , x 15 = 41 , x 21 = 1 , x 24 = 40 , x 32 = 11 , x 37 = 40 , x 46 = 5 , x 48 = 38 , x 51 = 34 , x 52 = 7 , x 63 = 22 , x 66 = 27 x_{12}=19,x_{15}=41,x_{21}=1,x_{24}=40,x_{32}=11,x_{37}=40,x_{46}=5,x_{48}=38,x_{51}=34,x_{52}=7,x_{63}=22,x_{66}=27x12=19,x15=41,x21=1,x24=40,x32=11,x37=40,x46=5,x48=38,x51=34,x52=7,x63=22,x66=27
matlab程序如下`
clc,clear
a=readmatrix('data1.txt') %读取表中的数据
%%若数据是整行整列的表,则可以用load('文件名')
c=a(1:end-1,1:end-1);
%%end表示行、列的最大值
d=a(end,1:end-1);
e=a(1:end-1,end);
x=optimvar("x",6,8,'LowerBound',0) %定义决策向量
prob=optimproblem('Objective',sum(c.*x,'all'));
%定义问题,并写出目标函数
%这里sum(c.*x,'all')相当于sum(sum(c.*x))
prob.Constraints.c1=sum(x)==d;
%sum(A),不指定dim或指定dim为1,则自动计算成所有列向量数值的和;如果指定dim为2,则自动计算成所有行向量数值的和
prob.Constraints.c2=sum(x,2)<=e;
[sol,fval,flag,out]=solve(prob)
xx=sol.x
writematrix(xx,'data1.xlsx') %把数据贴到excel表格中,用于做表使用
4.问题记录
模型建立方面:
1.模型要注意灵敏度分析,即分析哪个变量的轻微波动对结果的影响更大(现实生活中难免决策变量会发生变化)
2.投资偏好系数:投资者在权衡资产风险和预期收益两方面时,希望选择一个令自己满意的投资组合,因此对风险和收益分别赋予权重,s称为投资偏好系数
记风险为P,收益为Q,则需要寻找一个s,使得
m i n P − Q min P-QminP−Q,或m a x Q − P max Q-PmaxQ−P。
