应用numpy里的SVD实现3D直线拟合点云

缘起

只是求出了几何质心, 如何加权还不会…

问题:

对一组质心(点云)拟合直线, 这条线被称为:3D正交距离回归 (ODR) 线 (3D Orthogonal Distance Regression (ODR) line )

探索

奇异值分解（singular value decomposition, SVD）

(参见:奇异值分解 - 中文维基百科【维基百科中文版网站】)
?真心没看懂…

照搬算法:五步穿云法

def lineFitPoints(psarr):
	'''
	'''
	# 1. 求质心
	ct = np.mean(psarr, axis = 0)
	# 2. 减质心
	data = psarr-ct
	# 3. SVD
	_,_,vv = np.linalg.svd(data)
	# 4. 取线的矢量
	# 最大奇异值对应的右奇异向量...???‍♀️不知道啥意思
	drt = vv[0]
	# 5. 点(质心)+矢量得到直线
	length = len(psarr)+2 # 线的长度
	p3 = ct + vv[0] / np.linalg.norm(vv[0]) * length/2
	Helper.p2pexLine(p3,ct,modName="axis", plus = length/2) # Slicer项目里面专用

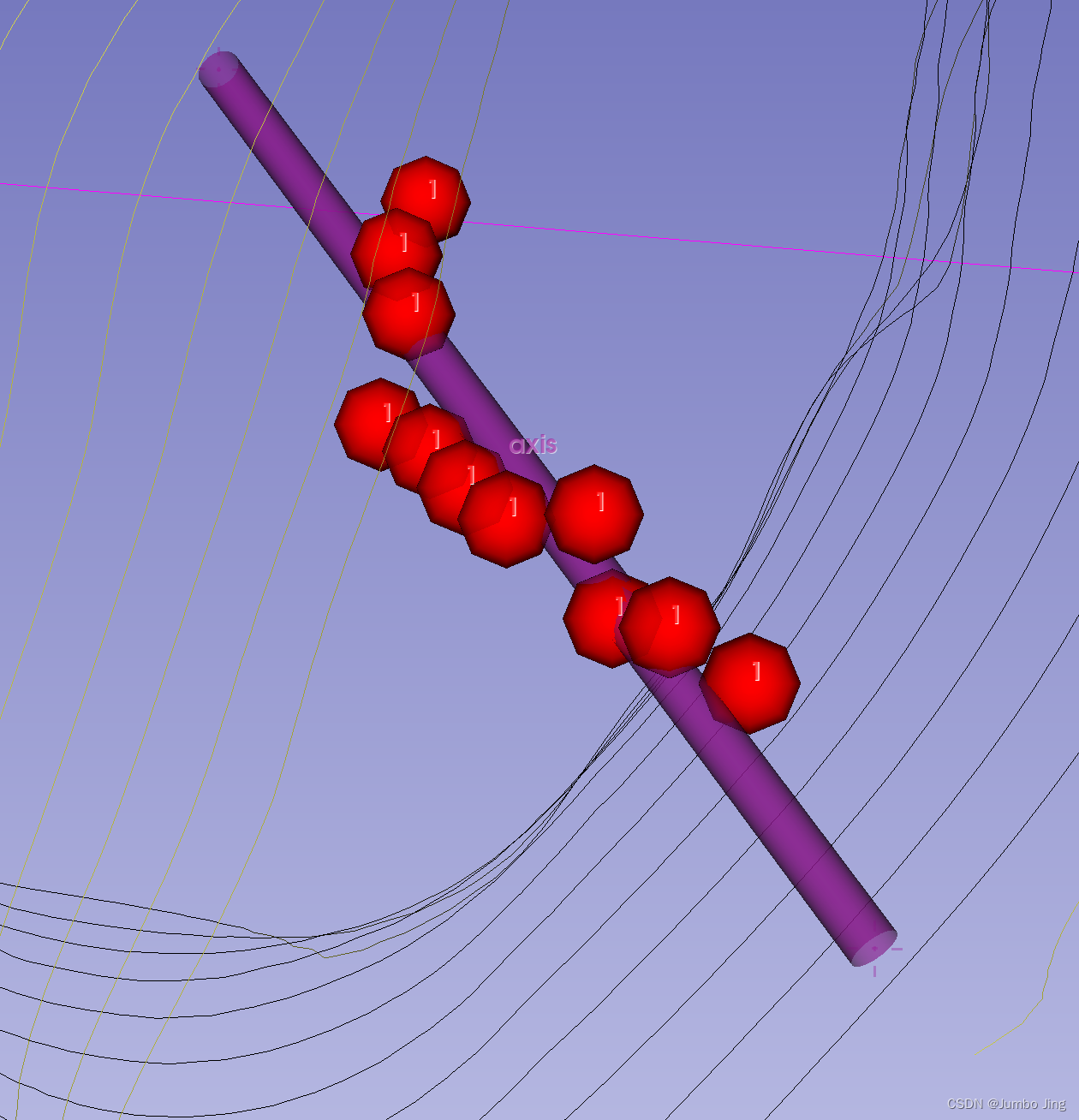
参考

3D Line Fitting in 5 Easy Steps with SVD – CodeFull
p2pexLine