动态规划算法

简单来说，就是把问题分成多个阶段，每个阶段都符合一个式子（状态转移），后面阶段的状态（结果）一般可以由前面阶段的状态（结果）转移而来。

找出状态转移方程，动态规划已经成功了 90%。使用动态规划求解时，最关键的是找出状态转移方程，而想要找出状态转移方程，首先要对问题状态有清晰的定义。一般来说，动态规划求解主要包括以下步骤：

• 划分阶段：把问题划分成子问题，类似于分治法，每个阶段一般是有序的。
• 定义状态：每个阶段，都有属于自己的最优状态，每一个阶段的最优状态，可以从前面阶段的最优状态中转化获得。
• 状态转化：不同阶段之间的转化关系，就是状态转移方程，定义好它们之间的递推关系，就是极其重要的一步。
• 逆向求解：一般来说我们要求解一个状态，需要先把前面的状态先求解。那么逆向就是自底向上，也就是先挨个把前面的- 状态求解，再使用前面的状态求解后面的状态。（注意最初的状态定义必须准确，边界值需要处理好）

斐波那契数列

public class FibonacciTest {

  public static int Fibonacci(int n) {
    if (n == 0) {
      return 0;
    }
    if (n == 1) {
      return 1;
    }
    int[] nums = new int[n + 1];
    nums[0] = 0;
    nums[1] = 1;
    for (int i = 2; i <= n; i++) {
      nums[i] = nums[i - 1] + nums[i - 2];
    }
    return nums[n];
  }
}

优化之后

public class FibonacciTest {

  public int Fibonacci(int n) {
    if (n <= 0) return 0;
    if (n == 1) return 1;
    // 初始化状态
    int fibonacci1 = 0;
    int fibonacci2 = 1;
    int result = 0;
    for (int i = 2; i <= n; i++) {
      result = fibonacci1 + fibonacci2;
      fibonacci1 = fibonacci2;
      fibonacci2 = result;
    }
    // 返回最后的状态
    return result;
  }
}

跳台阶
小时候，我们会在阶梯上跳，现在我们玩一个游戏，一次可以跳上 1 级台阶，也可以跳上 2 级…… 假设也可以跳上 n 级。求我们跳上一个 n 级的台阶总共有多少种跳法。

public class JumpFloorTest {

  public int jumpFloor(int target) {
    if (target <= 0) {
      return 0;
    }
    int[] nums = new int[target];
    nums[0] = 1;
    for (int i = 0; i < target; i++) {
      int sum = 1;
      for (int j = 0; j < i; j++) {
        sum += nums[j];
      }
      nums[i] = sum;
    }
    return nums[target - 1];
  }
}

上面的做法明显复杂度过高，那么我们改用动态规划的方式：

• 定义状态：f(n) 表示跳上 n 级台阶的方法。
• 初始化状态：跳上第一级只有一种方法，f(1) = 1。
  

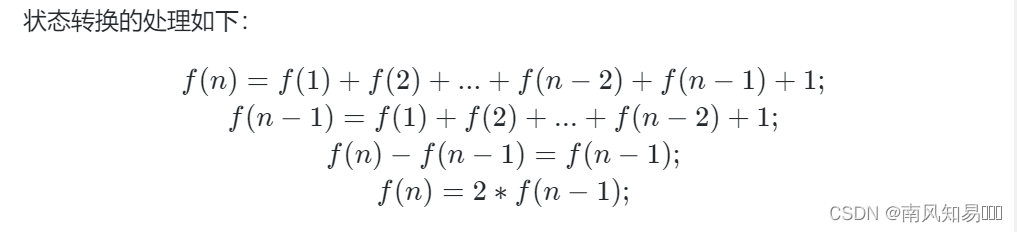
public class JumpFloorTest {

  public static void main(String[] args) {
    System.out.println("F(4) = " + jumpFloor(4));
  }

  public static int jumpFloor(int target) {
    if (target <= 0) return 0;
    // 初始化
    int total = 1;
    for (int i = 1; i < target; i++) {
      // 状态转移
      total = 2 * total;
    }
    return total;
  }
}

动态规划求解回文串

“上海自来水来自海上”，这句话不管是顺着读还是逆着读，都是一样的，这就是回文串。相信如何判断一个字符串是回文串，这个问题大家都会（根据中心对称来判断即可），现在问题升级了，给出一个字符串 s，找到 s 里面包含的最长的回文串。

输入：s = abddbc
输出：bddb

public class Palindrome {

  public static void main(String[] args) {
    System.out.println(longestPalindrome("abddbc"));
  }

  public static String longestPalindrome(String str) {
    int size = str.length();
    if (size <= 1) return str;
    boolean[][] results = new boolean[size][size];
    // 起始索引位置
    int startIndex = 0;
    // 保存回文串最大长度
    int max = 0;
    // 初始化状态，长度为 1 和 2 的子串
    for (int i = 0; i < size; i++) {
      results[i][i] = true;
      if (i < size - 1 && str.charAt(i) == str.charAt(i + 1)) {
        results[i][i + 1] = true;
        startIndex = i;
        max = 2;
      }
    }
    // 回文串的长度从 3 开始计算
    for (int length = 3; length <= size; length++) {
      for (int i = 0; i <= size - length; i++) {
        int j = i + length - 1;
        // 去掉当前字符的前面长度为 length 的子串是回文串，且当前字符与对折字符相等
        if (results[i + 1][j - 1] && str.charAt(i) == str.charAt(j)) {
          results[i][j] = true;
          startIndex = i;
          max = length;
        }
      }
    }
    print(results);
    if (startIndex == 0 && max == 0) return String.valueOf(str.charAt(0));
    // 返回回文串
    return str.substring(startIndex, startIndex + max);
  }

  // 打印矩阵
  public static void print(boolean[][] results) {
    for (int i = 0; i < results.length; i++) {
      for (int j = 0; j < results[0].length; j++) {
        System.out.print(results[i][j] ? "T " : "F ");
      }
      System.out.println("");
    }
    System.out.println("========================== ");
  }
}

连续子数组的最大和

假设有一个整型数组，数组里有正数也有负数。数组中的一个或连续多个整数组成一个子数组。现在要求所有子数组的和的最大值，当然我们还希望时间复杂度为 O(n)。

倘若没有时间复杂度的要求，我们马上就能想到暴力破解的方法，那就是两层循环，求每一个区间的子数组的和，不断和最大值比较，最后得到最大值。

public class LargeSumOfSubArray {

  public static void main(String[] args) {
    System.out.println("sum: " + simpleSolution(new int[] { 1, -3, 4, 2, -8 }));
  }

  public static int simpleSolution(int[] array) {
    if (array == null || array.length == 0) {
      return 0;
    }
    int result = Integer.MIN_VALUE;
    // 从每一个字符开始
    for (int i = 0; i < array.length; i++) {
      int tempSum = 0;
      // 每一种长度的子串（合法的索引范围）
      for (int j = i; j < array.length; j++) {
        tempSum = tempSum + array[j];
        // 当前最大值和保存的最大值相比较
        if (tempSum > result) {
          result = tempSum;
        }
      }
    }
    return result;
  }
}

暴力破解并非我们目的所在，我们需要尝试使用动态规划来解决它。动态规划三把斧，状态定义，初始化状态以及状态转换。动态规划只要找出状态转移方程，就意味着成功了一大半。

我们求解的是字符串里面的最大连续子数组之和，假设我们得知一个数组里面的最大子数组之和，还得知了这个数组后面的元素，可以知道这个数组加上这个元素之后的最大子数组之和么？

答案是否定的，因为我们不知道之前的数组的最大连续子数组之和，是否是以最后一个元素为结尾的，如果不是，我们加上新的元素，就不能算是连续子数组。因此这里面的状态除了最大的子数组之外，还有以最后一个元素为结尾的最大子数组之和。

定义状态：dp[i] 表示下标以 i 结尾的连续子数组的最大和，假设数组大小为 n，那么最终求解的就是 dp[n-1]。

• 以 num[i-1] 结尾的连续子数组最大和 max + 当前数 nums[i]。
• 连续子数组最大和还是之前的 dp[i-1]。
• 当前数 nums[i]。

状态转移方程为：

dp[i] = Max{ Max { max + nums[i] , nums[i] } , dp[i-1] }

public class LargeSumOfSubArray {

  public static void main(String[] args) {
    System.out.println(
      "sum: " + findLargeSumOfSubArray(new int[] { 1, -3, 4, 2, -8 })
    );
  }

  public static int findLargeSumOfSubArray(int[] array) {
    // 记录当前所有子数组的和的最大值
    int res = array[0];
    // 包含 array[i] 的连续数组最大值
    int max = array[0];
    for (int i = 1; i < array.length; i++) {
      // 当前元素加上以上一个元素结尾的连续子数组的和，与当前元素比较，去较大值
      max = Math.max(max + array[i], array[i]);
      // 更新保存的最大值
      res = Math.max(max, res);
    }
    return res;
  }
}

捡最大价值的装备包

你有一个背包，只能装 m 公斤，你现在刚刚降落，走进一个房子，房子里面有 n 个物品，假设每件物品的重量取值为 W1、W2、W3… Wn，每件物品对你的成长价值是 C1、C2、C3… Cn，所以这个时候，你要选择把最大价值的装备放到自己的背包里，那我们怎么选择呢？

• 定义状态：如果前面 i 件装备，放进最大重量为 w 的背包，获得的最大价值为 v[i][w]。
• 初始化状态：0 件装备或者背包的最大重量为 0 的背包，获得的最大的价值都是 0。
• 状态转移：面临第 i 件装备放不放进去这个问题，有两种情况：
  • 放进去的第 i 件装备，超过了最大的背包数量，放不进去，那么 v[i][w] = v[i-1][w]，也就是在最大的重量是 w 的背包里面，从前面 i 件挑选放进去最优解，和从前面 i-1 件中挑选的最优解是一样的。
  • 剩下的空间可以放下第 i 件，选择放进去，那么假设第 i 件物品的重量是 w[i]，此时的最优解，应该是 v - w[i] 大小的背包，选择放进去 i-1 件的最优解，再加上现在放进去的背包 c[i]。

总结一下：i 件物品放进容量为 V 的背包中的最优选择是取上面步骤 1 和 2 中最大的，也就是 Max{v[i-1][v],c[i-1][v-w[i]]+c[i]}。

public class BagValue {

  public static void main(String[] args) {
    int maxWeight = 10;
    int bagNum = 5;
    int[] weights = { 3, 4, 5, 7, 2 };
    int[] values = { 3, 5, 4, 6, 1 };
    int[][] results = bagValue(maxWeight, bagNum, weights, values);
    print(results);
  }

  public static int[][] bagValue(
    int maxWeight,
    int bagNum,
    int weights[],
    int values[]
  ) {
    // c[i][m] 表示前 i 件物品恰好放入重量为 m 的背包时的最大价值
    int v[][] = new int[bagNum + 1][maxWeight + 1];
    // 初始化状态，重量最大为 0，结果肯定为 0
    for (int i = 0; i < bagNum + 1; i++) {
      v[i][0] = 0;
    }
    // 初始化状态，包裹数量最大为 0，结果肯定为 0
    for (int j = 0; j < maxWeight + 1; j++) {
      v[0][j] = 0;
    }
    // 循环
    for (int i = 1; i < bagNum + 1; i++) {
      for (int j = 1; j < maxWeight + 1; j++) {
        // 规划到物品为 i 件最大重量为 j 时，如果第 i 件的重量 (weights[i-1]) 小于最大重量 j：
        if (weights[i - 1] <= j) {
          // 如果放进去的价值比不放进去的价值更大
          if (v[i - 1][j] < v[i - 1][j - weights[i - 1]] + values[i - 1]) {
            // 物品 i 放入背包中，则背包剩余重量为 j-weights[i-1]
            // 则 v[i][j] 为 v[i-1][j-weights[i-1]] 的值加上当前物品 i 的价值
            v[i][j] = v[i - 1][j - weights[i - 1]] + values[i - 1];
          } else {
            // 第 i 件不放入背包中，所以 v[i][j] 为 v[i-1][j] 的值
            v[i][j] = v[i - 1][j];
          }
        } else {
          v[i][j] = v[i - 1][j];
        }
      }
    }
    return v;
  }

  // 打印矩阵
  public static void print(int[][] results) {
    for (int i = 0; i < results.length; i++) {
      for (int j = 0; j < results[0].length; j++) {
        System.out.print(results[i][j] + " ");
      }
      System.out.println("");
    }
    System.out.println(
      "最大价值为： " + results[results.length - 1][results[0].length - 1]
    );
  }
}

最长公共子序列

字符串一般会涉及子序列和子串两个概念，子序列和子串可不是同样的概念，子串要求是连续的，而子序列只要求顺序并不要求连续。

我们可以知道这个问题可以分解为更小的问题，思考一下，比如长度为 n 的字符串 str1 和长度为 m 的字符串 str2，两者的最长公共子序列，是不是可以从 str1 前长度为 n-1 的子串与 str2 前长度为 m-1 的子串的最长公共子序列中得知呢？答案是肯定的。

public class LCS {

  public static void main(String[] args) {
    findLCS("abbcdd", "abdbcabd");
  }

  public static int findLCS(String str1, String str2) {
    int n = str1.length();
    int m = str2.length();
    // 状态定义
    int[][] dp = new int[n + 1][m + 1];
    // 初始化状态
    for (int i = 0; i <= n; i++) {
      for (int j = 0; j <= m; j++) {
        dp[i][j] = 0;
      }
    }
    for (int i = 1; i <= n; i++) {
      for (int j = 1; j <= m; j++) {
        // 如果两个字符相等
        if (str1.charAt(i - 1) == str2.charAt(j - 1)) {
          dp[i][j] = dp[i - 1][j - 1] + 1;
        } else {
          // 不相等的时候，取 dp[i - 1][j] 和 dp[i][j - 1] 的最大
          dp[i][j] = dp[i - 1][j] > dp[i][j - 1] ? dp[i - 1][j] : dp[i][j - 1];
        }
      }
    }
    print(dp);
    return dp[n][m];
  }

  // 打印矩阵
  public static void print(int[][] results) {
    for (int i = 0; i < results.length; i++) {
      for (int j = 0; j < results[0].length; j++) {
        System.out.print(results[i][j] + " ");
      }
      System.out.println("");
    }
    System.out.println(
      "最长公共子串的长度为： " +
      results[results.length - 1][results[0].length - 1]
    );
  }
}

寻找数字塔的路径

数字塔是一座由数字组成的塔，第 i 层由 i 个数字组成，比如下面的塔中，1 + 3 + 7 + 9 + 11 = 31 就是最大的路径值。最上面的 1 可以往下走到 3 或者 5，上面第 2 层的 3 又可以走到第三层的 7 或者 5，但是不能走到 2。

• 定义状态：dp[i][j] 表示走到第 i+1 层，第 j+1 个位置的最大路径值。
• 初始化状态：第一层的第一个位置的最大路径只有一种，就是塔的顶点位置的值，dp[0][0]=data[0][0]。
• 状态转换：每一个位置索引合法的情况下，只能通过自己的左上角或者右上角的位置走下来。那么就是 dp[i][j] = Math.max(dp[i-1][j-1], dp[i-1][j]) + data[i][j]，如果在左边界，那么只能是右上角走下来，也就是 dp[i][j] = dp[i-1][j] + data[i][j]，在求解的过程中，用变量保存最大值，不断更新即可。
  

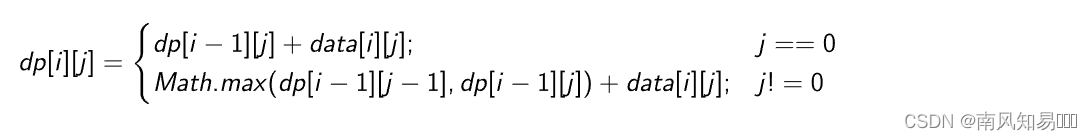
public class Tower {

  public static void main(String[] args) {
    int[][] datas = {
      { 1 },
      { 3, 5 },
      { 7, 5, 2 },
      { 9, 3, 4, 11 },
      { 11, 1, 2, 5, 7 },
    };
    System.out.println("最大路径为：" + maxRoute(datas));
  }

  public static int maxRoute(int data[][]) {
    int max = 0;
    int dp[][] = new int[data.length][data.length];
    dp[0][0] = data[0][0];
    for (int i = 1; i < data.length; i++) {
      for (int j = 0; j <= i; j++) {
        if (j == 0) {
          // 左边界，直接是右上角的数字相加
          dp[i][j] = dp[i - 1][j] + data[i][j];
        } else {
          // 不是左边界，取左上角也右上角的最大值
          dp[i][j] = Math.max(dp[i - 1][j - 1], dp[i - 1][j]) + data[i][j];
        }
        max = Math.max(dp[i][j], max);
      }
    }
    print(dp);
    return max;
  }

  // 打印矩阵
  public static void print(int[][] results) {
    for (int i = 0; i < results.length; i++) {
      for (int j = 0; j < results[0].length; j++) {
        System.out.print(results[i][j] + " ");
      }
      System.out.println("");
    }
  }
}