距离度量方法

距离定义

        假设有n维向量a、b、c，则定义距离满足以下三个条件：

1）非负性：d(a,b)>=0,当且仅当a=b时，d(a,b)=0;

2）对称性：d(a,b)=d(b,a);

3）三角不等式：d(a,b)<=d(a,c)+d(c,b)

距离度量方法

       在特征空间中，取出两个特征，它们分别是n维的特征向量

（1）明可夫斯基距离（闵可夫斯基距离）

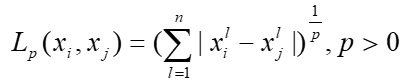
       明可夫斯基距离三种特殊而常见形式：曼哈顿距离、欧氏距离、切比雪夫距离（p=1、2、∞）。

       在明考夫斯基距离中，p值越大，其受（较大的）异常值影响就越厉害。可以发现当p=∞时，切比雪夫距离将完全由最大的异常值决定。同理，欧式距离比曼哈顿距离受异常值的影响程度更高。

（2）曼哈顿距离

（3）欧几里得距离

（4）切比雪夫距离

（5）马氏距离

S为协方差矩阵。