在一些应用问题中,需要将n个不同的元素划分成一些不相交的集合。开始时,每个元素自成一个单元素集
合,然后按一定的规律将归于同一组元素的集合合并。在此过程中要反复用到查询某一个元素归属于那个集
合的运算。
举例:求朋友圈
链接:https://www.nowcoder.com/questionTerminal/a5c097f75db8418395b6a0e32c608c38
假设有N个用户,其中有些人是朋友,有些则不是。A和B是朋友,B和C是朋友,这样ABC就是一个朋友圈,请计算给定的朋友关系的朋友圈数。
给定一个 N * N 的矩阵 M,表示用户之间的朋友关系。如果M[i][j] = 1,表示已知第 i 个和 j 个人互为朋友关系,否则为不知道。输出所有用户中的已知的朋友圈总数。
示例1
输入
3
1,1,0
1,1,0
0,0,1
输出
2
说明
第0个用户和第1个用户组成一个朋友圈,第2个用户组成一个朋友圈
这道题讲述就是有一组元素,他们相互之间产生某种关系,形成了集合,面对这种问题,有了并查集我们解决这类问题是较简单的。
下面就来研究下并查集。
其实就是一个数组,首先将数组所有值初始化为-1。
假设有5个人:下标分别为0-4,并初始化为-1 ,我们这里用负数表示自己为整体
0 1 2 3 4
-1 -1 -1 -1 -1
假设过了一段时间后,编号为0,2,4的同学形成了一个集合。编号为1,3的同学形成了一个集合。
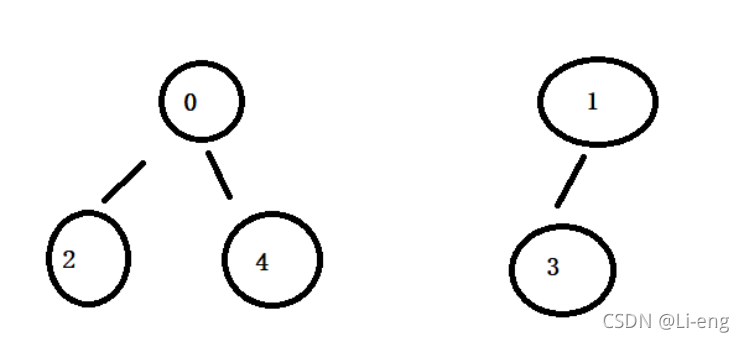
0 1 2 3 4
-3 -2 0 1 0
2 4的父亲为0,所以对应下标的值变为0
3 的父亲为1,所以对应下标的值变为1
0和1 本来是-1,为什么变了呢?
在这里我们规定,假如两个集合合并了,比如1和3合并,那么就把3这个集合所有的都要合并过来,也就是找到3的根节点(也就是自己),把1和3的根节点加起来,所以 3的值变成 1,而1的值变成了 -2.
用负数代表根,数字代表该集合中的元素个数
如果在进行合并,如图,合并0和1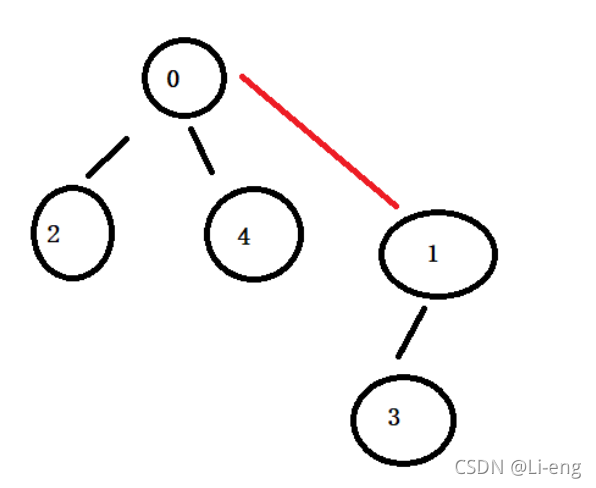
找到0的根,也就是0自己,将0成为新集合的头,并计算他的元素个数,
找到1的根,1的内容则指向0的索引
也就变成了
0 1 2 3 4
-5 0 0 1 0
通过以上例子可知,并查集一般可以解决一下问题:
- 查找元素属于哪个集合
沿着数组表示树形关系以上一直找到根(即:树中中元素为负数的位置) - 查看两个元素是否属于同一个集合
沿着数组表示的树形关系往上一直找到树的根,如果根相同表明在同一个集合,否则不在 - 将两个集合归并成一个集合
将两个集合中的元素合并
将一个集合名称改成另一个集合的名称 - 集合的个数
遍历数组,数组中元素为负数的个数即为集合的个数。
寻找某个元素的根节点:
因为根节点必定是负数,所以while循环,直到找到最上层的父亲,返回值。
int FindRoot(int x)
{
assert(x < _ufs.size());
while (_ufs[x] >= 0)
{
x = _ufs[x];
}
return x;
}
将两个集合合并的操作:
就是先找到两个元素的根节点,如果相等,说明在同一集合,否则
将root1成为新集合的头,并计算他的元素个数,root2的内容则指向root1的索引(也就是存的根节点索引)
bool Union(int x1,int x2)
{
int root1 = FindRoot(x1);
int root2 = FindRoot(x2);
if (root1 == root2)
return false;
else
{
//将root1成为新集合的头,并计算他的元素个数,root2的内容则指向root1的索引
_ufs[root1] += _ufs[root2];
_ufs[root2] = root1;
return true;
}
}
算出数组当中有多少个集合:
就是循环判断每个元素下标对应的值,负数则为根
int Size()
{
int count = 0;
for (int i = 0; i < _ufs.size(); ++i)
{
//计算数组中有几个集合
if (_ufs[i] < 0)
count++;
}
return count;
}
朋友圈题目解析
这题其实就是给了我们一个二维矩阵,然后让我们确定有多少个朋友圈,这个就很简单了,我们可以遍历一遍数组,用我们的Union的接口将两个人合并成一个集合,最后在用Size接口来计算集合的个数。
class UnionFindSet
{
public:
UnionFindSet(int x)
{
_ufs.resize(x, -1);
//初始化的时候讲x个空间初始化成-1
}
bool Union(int x1,int x2)
{
int root1 = FindRoot(x1);
int root2 = FindRoot(x2);
if (root1 == root2)
return false;
else
{
//将root1成为新集合的头,并计算他的元素个数,root2的内容则指向root1的索引
_ufs[root1] += _ufs[root2];
_ufs[root2] = root1;
return true;
}
}
int FindRoot(int x)
{
assert(x < _ufs.size());
while (_ufs[x] >= 0)
{
x = _ufs[x];
}
return x;
}
int Size()
{
int count = 0;
for (int i = 0; i < _ufs.size(); ++i)
{
if (_ufs[i] < 0)
count++;
}
return count;
}
private:
vector<int> _ufs;
};
class Solution {
public:
int findCircleNum(vector<vector<int>>& isConnected) {
UnionFindSet ufs(isConnected.size());
for(int i =0;i<isConnected.size();++i)
{
for(int j =0;j<isConnected.size();++j)
{
//遍历二维数组,将 i==j自己与自己的情况过滤
if(i == j)
continue;
//1为朋友,将这两个人合并到一个集合
if(isConnected[i][j]==1)
ufs.Union(i,j);
}
}
int ret = ufs.UfsSize();
return ret;
}
};