跳表介绍

跳表(SkipList，全称跳跃表)是用于有序元素序列快速搜索查找的一个数据结构，跳表是一个随机化的数据结构，实质就是一种可以进行二分查找的有序链表。

跳表在原有的有序链表上面增加了多级索引，通过索引来实现快速查找。跳表不仅能提高搜索性能，同时也可以提高插入和删除操作的性能。它在性能上和红黑树，AVL树不相上下，但是跳表的原理非常简单，实现也比红黑树简单很多。

应用：**Redis的有序集合(zset) **

关于链表

链表的优势就是更高效的插入、删除。痛点是查询很慢，查询时间复杂度为O(n)。

跳表优化思路

以空间换时间，在链表基础上加几层索引，在查询某个节点的时候，首先会从上一层快速定位节点所在的一个范围，如果找到具体范围向下然后查找代价很小，当然在表的结构设计上会增加一个向下的索引(指针)用来查找确定底层节点。

这样链表便拥有了二分查找的查询性能(O(log n))。

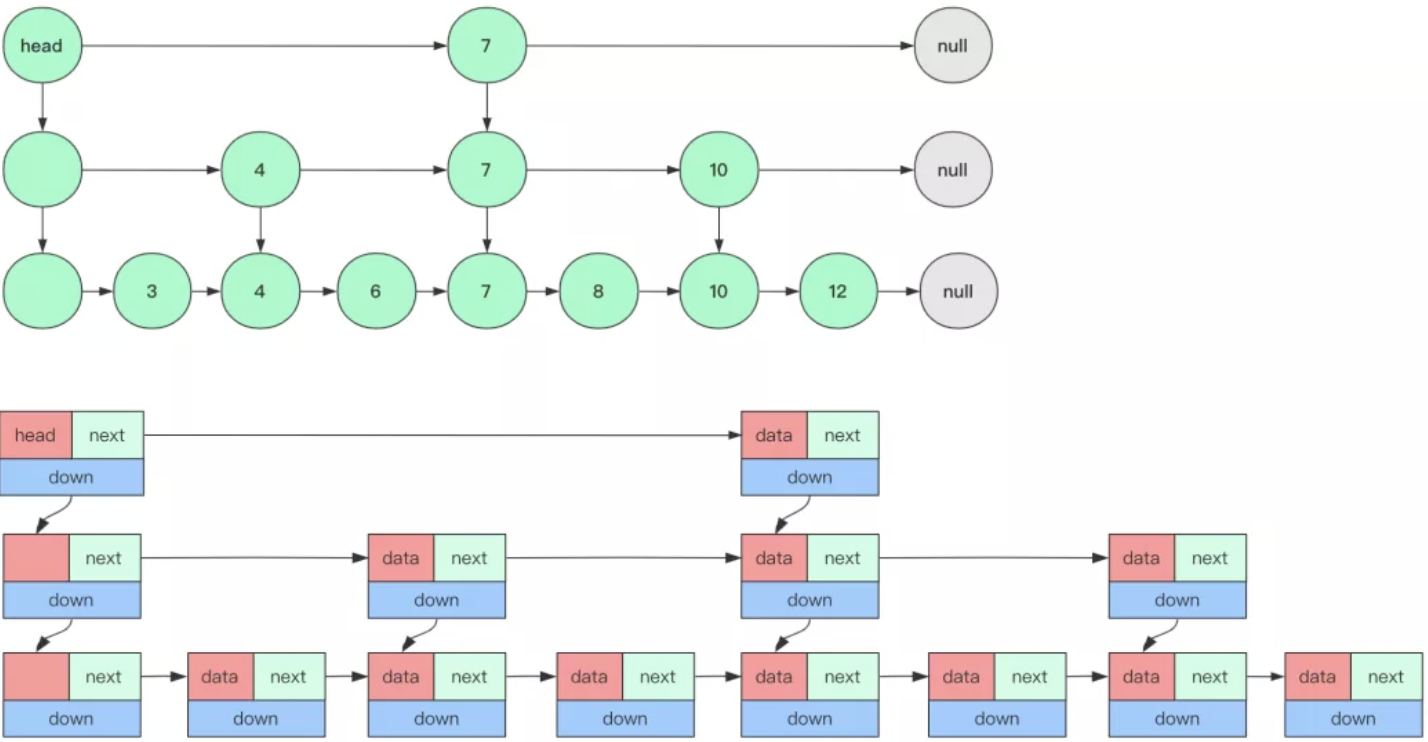
具体实现

跳表节点定义

/**
 * 节点定义
 */
private class Node {

    //节点key
    private int key;

    //节点value
    private T value;

    //同一层指向后继
    private Node next;

    //指向下层节点
    private Node down;

    public Node(int key, T value) {
        this.key = key;
        this.value = value;
    }
}

跳表定义

/**
 * 跳跃表数据结构
 */
public class SkipList<T> {
    //跳表头结点，不存储任何数据
    private Node head;

    //随机生成器/骰子 用于随机决定是否生成索引节点
    private Random random;

    //当前索引层数
    private int highLevel;

    //最大索引层数 用于控制索引层数
    private final int MAX_LEVEL = 1 << 5;

    public SkipList() {
        this.random = new Random();
        this.highLevel = 0;
        this.head = new Node(Integer.MIN_VALUE, null);
    }
    
    ......
}

查

public T search(int key) {
    Node node = searchNode(key);
    return node == null ? null : node.value;
}

private Node searchNode(int key) {
    Node node = head;
    while (node != null) {
        //本层未找到该值 or 索引，则到下层找
        if (node.next == null) {
            node = node.down;
        } else if (node.next.key == key) {
            //本层找到该值 or 索引
            return node.next;
        } else if (node.next.key > key) {
            //本层找到该值 or 索引
            node = node.down;
        } else {
            //当前节点比查找值小，继续在本层查找
            node = node.next;
        }
    }
    return null;
}

改

public void modify(int key, T value) {
    Node node = searchNode(key);
    //与查询不同的是，修改需要将该值的所有索引节点都修改掉
    //该值的所有索引节点必然可以通过down指针索引到
    if (node != null) {
        node.value = value;
        node = node.down;
        while (node != null) {
            node.value = value;
            node = node.down;
        }
    }
}

删

public T delete(int key) {
    Node node = head;
    T value = null;
    while (node != null) {
        if (node.next == null) {
            node = node.down;
        } else if (node.next.key == key) {
            value = node.next.value;
            node.next = node.next.next;
            //删除和修改有点类似，需要将该值所有索引都删除
            node = node.down;
        } else if (node.next.key > key) {
            node = node.down;
        } else {
            node = node.next;
        }
    }
    return value;
}

增

public void add(int key, T value) {
    Node node = head;
    //这个栈用于记录将要插入节点的前驱节点
    Stack<Node> stack = new Stack<>();
    while (node != null) {
        if (node.next == null) {
            //插入位置在下一层，但是后面如果要插入的话，
            //当前这个节点后也可能要插入
            stack.add(node);
            node = node.down;
        } else if (node.next.key == key) {
            //key存在，直接覆盖更新
            node.next.value = value;
            node = node.next.down;
            while (node != null) {
                node.value = value;
                node = node.down;
            }
            return;
        } else if (node.next.key > key) {
            //插入位置在下一层，但是后面如果要插入的话，
            //当前这个节点后也可能要插入
            stack.add(node);
            node = node.down;
        } else {
            //查找插入位置
            node = node.next;
        }
    }

    //记录索引层前驱
    Node preNode = null;
    //记录当前处理层数，防止层数超过限制
    int level = 1;
    do {
        //处理最底下一层 or 处理索引层
        Node pop = stack.pop();
        Node n = new Node(key, value);
        n.next = pop.next;
        n.down = preNode;
        pop.next = n;
        //记录索引层前驱
        preNode = n;
        //随机是否向上层添加索引
        if (random.nextBoolean()) {
            break;
        }
        level ++;
        //如果当前处理层数超过限制，那么停止向上添加索引层
        if (level > MAX_LEVEL) {
            break;
        }
        //如果当前处理层数未超过限制，但是超过当前已添加的最高层
        //则需要向上新建一层
        if (level > highLevel) {
            highLevel = level;
            n = new Node(Integer.MIN_VALUE, null);
            n.down = head;
            //向上新建一层索引层
            head = n;
            //接下来需要在这新增的索引层上添加索引节点
            stack.add(n);
        }
    } while (!stack.isEmpty());
}

跳表展示

public void print() {
    Node teamNode = head;
    int index = 1;
    Node last = teamNode;
    while (last.down != null){
        last = last.down;
    }
    while (teamNode != null) {
        Node enumNode = teamNode.next;
        Node enumLast = last.next;
        System.out.printf("%-8s", "head->");
        while (enumLast != null && enumNode != null) {
            if(enumLast.key == enumNode.key) {
                System.out.printf("%-5s", enumLast.key + "->");
                enumLast = enumLast.next;
                enumNode = enumNode.next;
            } else {
                enumLast = enumLast.next;
                System.out.printf("%-5s", "");
            }
        }
        teamNode = teamNode.down;
        index ++;
        System.out.println();
    }
}

测试

public static void main(String[] args) {
    SkipList<Integer> list = new SkipList<>();
    for(int i = 1; i < 20; i ++) {
        list.add(i, 666);
    }
    System.out.println("删除前：");
    list.print();
    list.delete(4);
    list.delete(8);

    System.out.println("删除后：");
    list.print();
}

输出:

删除前：
head->  1->  
head->  1->                                                                             17-> 
head->  1->                                                                             17-> 
head->  1->       3->       5->                           11->                     16-> 17-> 18-> 19-> 
head->  1->       3->       5->       7->                 11->                15-> 16-> 17-> 18-> 19-> 
head->  1->  2->  3->  4->  5->  6->  7->  8->  9->  10-> 11-> 12-> 13-> 14-> 15-> 16-> 17-> 18-> 19-> 
删除后：
head->  1->  
head->  1->                                                                   17-> 
head->  1->                                                                   17-> 
head->  1->       3->  5->                      11->                     16-> 17-> 18-> 19-> 
head->  1->       3->  5->       7->            11->                15-> 16-> 17-> 18-> 19-> 
head->  1->  2->  3->  5->  6->  7->  9->  10-> 11-> 12-> 13-> 14-> 15-> 16-> 17-> 18-> 19-> 

参考：

高频面试数据结构——跳表