最小生成树及Prim算法及Kruskal算法的代码实现

最小生成树的概念

一个连通图的生成树是原图的最小连通子图，它包含原图中的所有顶点，而且有尽可能少的边。那么对生成树来说，若砍去它的一条边，生成树就会变成非连通图；若增加一条边，则图中会形成回路。

对于联通网络（带权连通图），构造最小生成树的准则有以下三条：
1、 有n个顶点的生成树有且仅有n-1条属于该网络的边来联结所有顶点；
2、 不能使用产生回路的边；
3、 树的总代价达到最小，即树中所有边的权值总和达到最小。

构造最小生成树的方法

构造最小生成树主要有两大类方法：

<1> 避圈法。按边的权值，从小到大依次添加边到生成树中，如果构成圈则不选。这类构造最小生成树的方法主要有：Prim算法、Kruskal算法和Solin算法。

<2> 破圈法。按边的权值，删除圈中权值最大的边。这类构造最小生成树的方法主要有Dijkstra算法。

关于这些算法的基本思想不再赘述，本文主要解决Prim算法和Kruskal算法的代码实现。

Prim算法

Prim算法是逐步选点的算法，适用于边稠密的图，并且宜选用邻接矩阵存储。

设一个有n个顶点的带权连通图G=(V,E)采用邻接矩阵存储，其最小生成树为T=(U,E’)，则从指定顶点v开始构造图G的最小生成树T的步骤如下：
1、初始化：U={v}，检查G.Edge[v][i]，将其中所有非0非∞的边<v, i>作为侯选边；
2、循环n-1次下面的操作，每次向U中加入一个顶点，向E‘中加入一条边：
①从侯选边中选择权值最小的边，设该边属于V-U的端顶点为k，让U = U∪{k}，将该边加入E’。
②检查所有属于V-U的顶点，将所有一个端顶点属于V，另一个端顶点属于V-U的边加入侯选边。
3、当U=V时算法结束，从T中得到图G的最小生成树。

实现代码：

1、构造邻接矩阵存储的带权无向图：

#define maxvertexnum 30 //最大顶点数
#define maxweight 0x3f3f3f3f //最大权值，相当于∞

//邻接矩阵存储的图
typedef struct{
    int Vertex[maxvertexnum]; //顶点表
    int Edge[maxvertexnum][maxvertexnum]; //边表、邻接矩阵
    int vexnum, edgenum; //图中顶点数、边数
}MGraph;

//构造带权无向图
void CreateMGraph(MGraph &G, int v[], int n, int edge[][3], int e){
    //初始化
    G.vexnum = n;
    G.edgenum = e;
    for(int i=0; i<G.vexnum; i++){
        G.Vertex[i] = v[i]; //初始化边表
        for(int j=0; j<G.vexnum; j++){
            G.Edge[i][j] = (i==j) ? 0 :maxweight;
        }
    }
    for(int i=0; i<G.edgenum; i++){
        int j = edge[i][0];
        int k = edge[i][1];
        G.Edge[j][k] = edge[i][2]; //形成邻接矩阵
        G.Edge[k][j] = edge[i][2];
    }
}

2、最小生成树的类型定义

//最小生成树的类型定义
typedef struct{ //最小生成树边结点的结构定义
    int v1, v2; //端顶点
    int value; //权值
}MSTEdgeNode; 
typedef struct{
    MSTEdgeNode edgeValue[maxvertexnum]; //用边值数组表示树
    int n; //数组中当前元素个数
}MST;

3、Prim算法的实现

//从顶点v出发用Prim算法构造图G的最小生成树
void PrimMGraph(MGraph &G, MST &T, int v){ 
    int visited[maxvertexnum]; //访问标记数组
    int k = 0; //数组元素个数
    for(int i=0; i<G.vexnum; i++) visited[i] = 0; //初始化标记数组
    for(int i=0; i<G.vexnum; i++){   //从第v行选,0到k-1为侯选边
        if(G.Edge[v][i]>0 && G.Edge[v][i]<maxweight){
            T.edgeValue[k].v1 = v;
            T.edgeValue[k].v2 = i;
            T.edgeValue[k++].value = G.Edge[v][i];
        }
    }
    T.n = k; //此时数组当前元素个数为k
    int minval, minpos;
    for(int i=0; i<G.vexnum-1; i++){ //重复n-1次选最小边
        minval = T.edgeValue[i].value;
        minpos = i;
        for(int j=i+1; j<T.n; j++){ //从i到k-1检查侯选边
            if(T.edgeValue[j].value < minval){
                minval = T.edgeValue[j].value;
                minpos = j; //最小权值在edgeValue[minpos]
            }
        }
        visited[T.edgeValue[minpos].v1] = 1;
        int u = T.edgeValue[minpos].v2; //最小权值边的终顶点
        for(int j=0; j<G.vexnum; j++){ //修改侯选边集合
            if(G.Edge[u][j]>0 && G.Edge[u][j]<maxweight && !visited[j]){
                T.edgeValue[k].v1 = u;  //增加依附于u的新侯选边
                T.edgeValue[k].v2 = j;
                T.edgeValue[k++].value = G.Edge[u][j];
                T.n++;
            }
        }
        if(i != minpos){  //最小权值边交换到T[i]
            MSTEdgeNode temp = T.edgeValue[i];
            T.edgeValue[i] = T.edgeValue[minpos];
            T.edgeValue[minpos] = temp;
        }
    }
    T.n = G.vexnum-1; //最终最小生成树有n-1条边
}

4、 主函数及调用

int main(){
    MGraph G;
    MST T;
    int n,e;
    cin>>n>>e; //输入结点数和边数
    int v[n], edge[e][3];
    for(int i=0; i<n; i++){
        cin>>v[i];
    }
    for(int i=0; i<e; i++){ //输入边及对应权值
        cin>>edge[i][0]>>edge[i][1]>>edge[i][2];
    }
    CreateMGraph(G, v, n, edge, e);
    cout<<endl;
    //输出邻接矩阵
    for(int i=0; i<G.vexnum; i++){
        for(int j=0; j<G.vexnum; j++){
            if(G.Edge[i][j] == maxweight){
                cout<<"∞"<<" ";
            }else
                cout<<G.Edge[i][j]<<" ";
        }
        cout<<endl;
    }
    cout<<endl;
    PrimMGraph(G, T, 0);
    //输出最小生成树的边及权值
    for(int i=0; i<T.n; i++){
        cout<<T.edgeValue[i].v1<<" "<<T.edgeValue[i].v2<<" "<<T.edgeValue[i].value<<endl;
    }
    return 0;
}

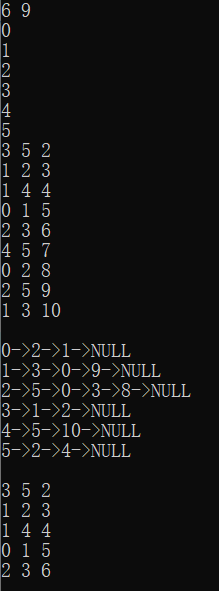
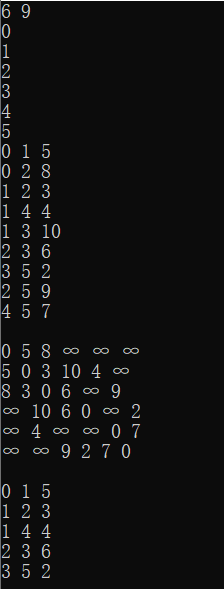
输入及运行结果：

Kruskal算法

Kruskal算法是逐步选边的算法，适用于稀疏图，并宜选用邻接表存储。

设一个有n个顶点的带权连通图G=(V,E)采用邻接表存储，其最小生成树为T=(U,E’)，则构造图G的最小生成树T的步骤如下：
1、 初始化：U=V，即包含图G中的所有顶点，E’为空，使得图中每一个顶点自成一个连通分量。同时，把图G中的所有边按照权值大小从小到大排列。
2、 重复执行以下步骤，直到有n-1条边加入到最小生成树：
①依次从小到大选择权值最小的边。
②检查当前选择的边的两个端顶点：
若两个端顶点属于不同的连通分量，则连通它们，并将它们加入生成树的顶点集合U，同时将该边加入E‘。
若两个端顶点属于同一个连通分量，则将该边舍弃，不加入最小生成树。
3、 算法结束，在T中得到图G的最小生成树。

实现代码：

1、 构造邻接矩阵存储的带权无向图。

#define maxvertexnum 30

//邻接表存储
typedef struct ENode{ //边表结点
    int adjvex; //邻接点存储位置
    struct ENode *nextarc; 
    int weight; //权值
}EdgeNode;
typedef struct VNode{ //顶点表结点
    int data; //顶点值
    struct ENode *firstarc; //指向邻接的第一条边
}VertexNode;
typedef struct{
    VertexNode VertexList[maxvertexnum]; //顶点表
    int vexnum, edgenum;
}ALGraph;

//构建带权无向图
void CreateALGraph(ALGraph &G, int v[], int n, int edge[][3], int e){
    //初始化
    G.vexnum = n;
    G.edgenum = e;
    for(int i=0; i<G.vexnum; i++){
        G.VertexList[i].data = v[i];
        G.VertexList[i].firstarc = NULL;
    }
    for(int i=0; i<G.edgenum; i++){ //头插法建立邻接表
        EdgeNode *p ,*q;
        int j = edge[i][0];
        int k = edge[i][1];
        q = G.VertexList[j].firstarc;
        p = (ENode *)malloc(sizeof(ENode));
        p->adjvex = k;
        p->nextarc = q;
        p->weight = edge[i][2];
        G.VertexList[j].firstarc = p;
        //无向图，k->j也需添加边
        q = G.VertexList[k].firstarc;
        p = (ENode *)malloc(sizeof(ENode));
        p->adjvex = j;
        p->nextarc = q;
        p->weight = edge[i][2];
        G.VertexList[k].firstarc = p;
    }
}

2、 最小生成树的结构定义

//最小生成树的类型定义
typedef struct{ //最小生成树边结点的结构定义
    int v1, v2; //端顶点
    int value; //权值
}MSTEdgeNode; 
typedef struct{
    MSTEdgeNode edgeValue[maxvertexnum]; //用边值数组表示树
    int n; //数组中当前元素个数
}MST;

3、 并查集操作

实现Kruskal算法需要用到并查集的操作，若要进一步了解并查集的细节，请参考文章树的应用——并查集及实现代码

//并查集操作
//初始化
void Init(int n, int father[], int height[]){
    for(int i=0; i<n; i++){
        father[i] = i; //每个结点的父结点为自身
        height[i] = 0; //每个结点的高度为0
    }
}
//查找
int Find(int father[], int x){
    if(x != father[x]){
        father[x] = Find(father, father[x]);
    }
    return father[x];
}
//合并
void Merge(int x, int y, int father[], int height[]){
    x = Find(father, x);
    y = Find(father, y);
    if(x != y){ //矮树作为高数的子树
        if(height[x] < height[y]){
            father[x] = y;
        }else if(height[x] > height[y]){
            father[y] = x;
        }else{
            father[y] = x;
            height[x]++;
        }
    }
}

4、 Kruskal算法的实现

//为简化操作，假设该图的所有边都按照权值从小到大依次存放在顺序表ev[]中，输入边时按照从小到大的顺序输入，并依次存入ev[]中
void KruskalMST(MSTEdgeNode ev[], int n, int e, MST &T){
    T.n = 0;
    int count = 0; //记录当前生成树的边数
    int i=0;
    int father[n];
    int height[n];
    Init(n, father, height);
    while(count<n-1){
        int u = Find(father, ev[i].v1);
        int v = Find(father, ev[i].v2);
        if(u != v){
            T.edgeValue[T.n++] = ev[i];
            Merge(u,v,father,height);
            count++;
        }
        i++;
    }
    if(count>=n) cout<<"该图不连通！"<<endl;
    else{
        for(int i=0; i<T.n; i++){
            cout<<T.edgeValue[i].v1<<" "<<T.edgeValue[i].v2<<" "<<T.edgeValue[i].value;
            cout<<endl;
        }
    }
}

5、 主函数及函数调用

int main(){
    ALGraph G;
    MST T;
    int n,e;
    cin>>n>>e;
    int v[n], edge[e][3];
    MSTEdgeNode ev[n];
    
    for(int i=0; i<n; i++){
        cin>>v[i];
    }
    for(int i=0; i<e; i++){
        cin>>edge[i][0]>>edge[i][1]>>edge[i][2];
        ev[i].v1 = edge[i][0];
        ev[i].v2 = edge[i][1];
        ev[i].value = edge[i][2];
    }
    CreateALGraph(G, v, n, edge, e);
    //输出邻接表
    for(int i=0; i<n; i++){
        EdgeNode *p = G.VertexList[i].firstarc;
        cout<<G.VertexList[i].data<<"->";
        while(p!=NULL){
            cout<<p->adjvex<<"->";
            p = p->nextarc;
        }
        cout<<"NULL"<<endl;
    }
    KruskalMST(ev, n, e, T);
    return 0;
}

说明：其实在实现kruskal算法时并未真正用到邻接表，这是因为我们为了简化操作，在输入时对边的权值进行了排序。若一开始输入的边并未进行排序，则需要遍历邻接表将边的权值进行排序，再依次存入到顺序表ev[]中。

运行结果：