首先:
1)数据有哪些类型?
离散数据,即数据的取值是不连续的。例如抛硬币
连续数据,它能取任意的数值,无限分割。例如时间
2)分布?
数据在统计图中的形状,称之为分布。
3)概率
概率分布就是在统计图中表示概率,横轴是数据的值,纵轴是横轴上对应数据值的概率。
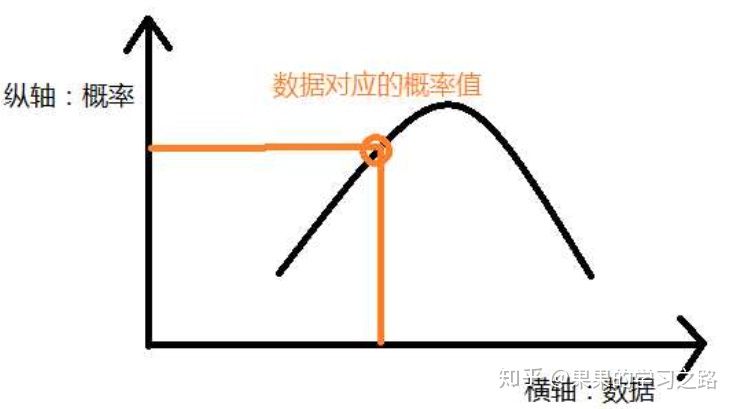
根据数据类型的不同,概率分布分为两种:离散概率分布,连续概率分布
对于离散概率分布,我们关心的是一个特定数值的概率。
对于连续概率分布,我们无法给出每一个数值的概率。
常见的4种概率分布:
1)3种离散概率分布
二项分布:
3个特点—做某件事的次数(也叫试验次数)是固定的,用n表示;
每一次事件都有两个可能的结果(成功,或者失败)
每一次成功的概率都是相等的,成功的概率用p表示
你感兴趣的是成功x次的概率是多少。
公式:
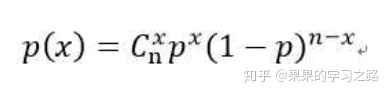
期望:E(X)=np (表示某事件发生n次,预期成功多少次)
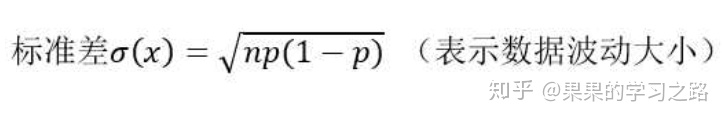
期望的含义:
在任何事情之前,知道预期结果对后面的决策有帮助。如你抛硬币5次,每次概率是1/2,那么期望E(X)=5*(1/2)=2.5次,即有大约3次可以抛出正面。
在比如你之前投资的那5支股票,假设每只股票帮你赚钱的概率是80%,那么期望E(X)=5*80%=4,也就是预期有4只股票投资成功帮你赚钱。
几何分布
即尝试多次能取得第一次成功的概率,就需要几何分布。
4个特点—做某件事的次数(也叫试验次数)是固定的,用n表示;
每一次事件都有两个可能的结果(成功,或者失败)
每一次成功的概率都是相等的,成功的概率用p表示
你感兴趣的是,进行X次尝试这个事情,取得第一次成功的概率是多大。
公式:
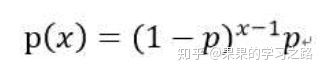
p为成功概率,即为了在第X次尝试取得第一次成功,首先需要你失败(X-1)次。
期望:E(X)=1/P
标准差=(1-P)/(P^2)
泊松分布
3个特点—事件是独立事件
在任意相同的时间范围内,事件发的概率相同
你想知道某个时间范围内,发生某件事情X次的概率是多大
用x代表事件发生的次数,u代表给定时间范围内事件发生的平均次数,概率计算公式为:
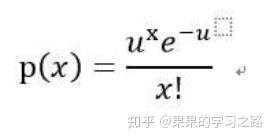
期望,方差为u
2)1种连续概率分布
正态分布