写在前面的话：
期末复习展开，为了方便大家更好的“预习”线性代数，考试完美过关，我们推出“七天期末线性代数急速突破栏目”
这个栏目将线性代数分为六个章节：每个章节分为两个系列：考试不挂，提升拔高
考试不挂系列是线性代数基础知识和基础习题的汇总，只要大家认真看认真学习，可以轻轻松松保证考试不挂科
提升拔高系列是线性代数拓展知识和拔高习题的汇总，难度较高，知识点更加深入，是为了让大家在期末考试突破90分冲刺满分
前期回顾：
爱学习的XP：七天期末线性代数急速突破——行列式篇（考试不挂）zhuanlan.zhihu.com
一、矩阵
（一）基本概念
形如
（二）一些特殊矩阵
1、单位矩阵
从左上角到右下角的对角线（称为主对角线）上的元素均为1。除此以外全都为0
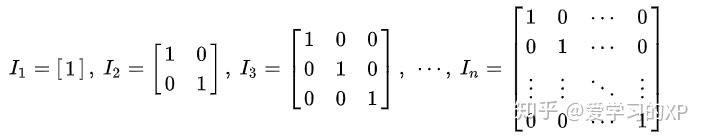
2、分块矩阵
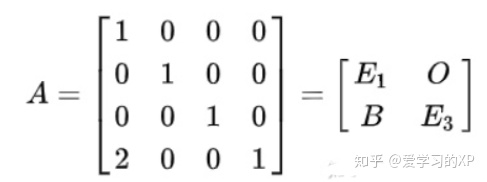
3、对称矩阵
设
4、反称矩阵
设
5、对角矩阵
除主对角线外其余数字均为0的矩阵，称为对角矩阵，记
6、准对角矩阵：是一种特殊的分块矩阵
7、上三角矩阵：主对角线以下都是零的方阵称为上三角矩阵
8、下三角矩阵：主对角线以上都是零的方阵称为下三角矩阵
9、转置矩阵：将矩阵的行列互换得到的新矩阵称为转置矩阵。例如：
设
矩阵转置的性质：
如果，那么
10、伴随矩阵
设
（三）矩阵的基本性质
1、矩阵相等：两个矩阵的对应位置上的元素都一一相等
2、同型矩阵：两个矩阵行数与列数相同
3、矩阵的初等行变换
（1）互换矩阵A的第i行与第j行，记为
（2）用非零常数h乘A的第i行，记为
（3）A的第i行的k倍加到第j行上，记为
4、矩阵A的初等列变换
（1）互换A的第i列与第j列
（2）A的第i列乘以非零常数h
（3）A的第i列的k倍加到第j列上
5、矩阵加减法
6、矩阵的数乘
设
7、矩阵与矩阵的乘法
设
注：两个矩阵可以相乘的充要条件为前乘矩阵的列数等于后乘矩阵的行数，两个矩阵相乘后的矩阵行数等于前乘矩阵的行数，列数等于后乘矩阵的列数（即
例如：
8、矩阵的乘方：设m为正整数，
（四）矩阵运算的性质
1、矩阵的加法和数乘运算统称为矩阵的线性运算
2、矩阵的加法和数乘满足交换律，结合律和分配律
3、只有矩阵A的列数等于矩阵B的行数，A与B的乘积AB才有意义
4、A与B的乘积AB继承了左边矩阵A的行数，右边矩阵B的列数
5、如果A=0或者B=0，那么AB=0,反之不一定成立
6、如果 A的第i行为零行，那么AB的第i行为零行，如果B的第j列为零列，那么AB的第j列为零列。
7、AB的非零行个数小于等于A的非零行个数，AB的非零列个数小于等于B的非零列个数
8、矩阵的乘法满足结合律和分配律，不满足交换律.A与B可以相乘，B与A不一定可以相乘.
9、矩阵乘法也不满足消去律，即AB=AC，且
10、关于矩阵乘方的性质
如果A为 方阵，s,t为非负整数，那么
如果A,B为同阶方阵，m为正整数。 如果AB可以交换，即AB=BA,那么前提很重要）
二、三个初等矩阵及其性质
（1）
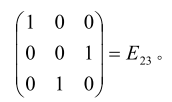
（2）
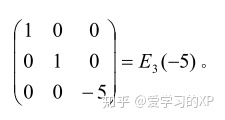
（3）
（4）性质：
综上我们可以看出：左乘一个初等矩阵相当于对矩阵做一个初等行变换，右乘一个初等矩阵相当于对矩阵做一个初等列变换。（左行右列）
三、矩阵的两大核心（逆阵与秩）
（一）：逆矩阵
1、逆矩阵
设
例如：设
解：
则
2、设
3、逆矩阵的性质
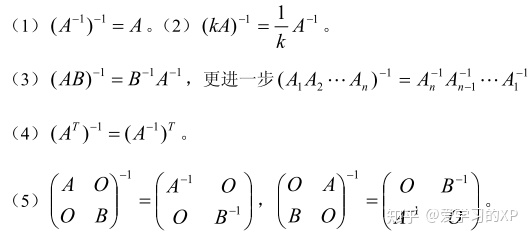
4、逆矩阵的求法
（1）伴随矩阵法：
（2）初等变换法：
一般来说，我们经常使用第二种方法：
1）构造n×（2n）矩阵
2）用初等行变换将
3）写出
例如：
解：1）构造矩阵
2）用初等行变换将
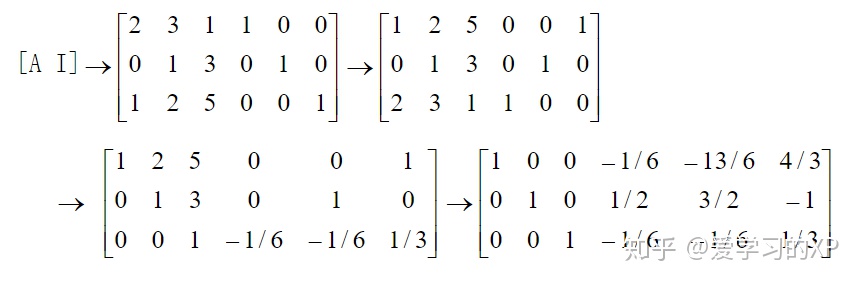
我们使用初等行变换的目的是使原矩阵（即左边的矩阵）变为初等矩阵
3)写出
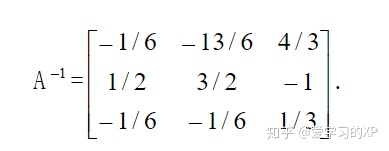
（二）矩阵的秩
1、矩阵的秩
设
2、矩阵秩的求法
将矩阵
3、矩阵秩的性质
口诀：矩阵的乘法不会使矩阵的秩升高
感谢@小季不是咸鱼对本系列的大力支持
经典题型讲解：
1、利用矩阵的三则运算求未知矩阵
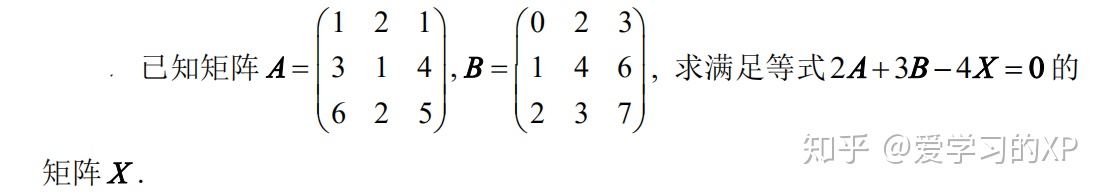
解：
2.利用待定系数法求矩阵（一般只是二阶）
解：
3.用结合律求矩阵的n次方
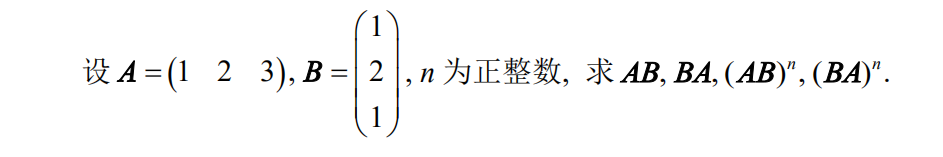
解：
4.用矩阵与初等矩阵的乘积表示行列变换
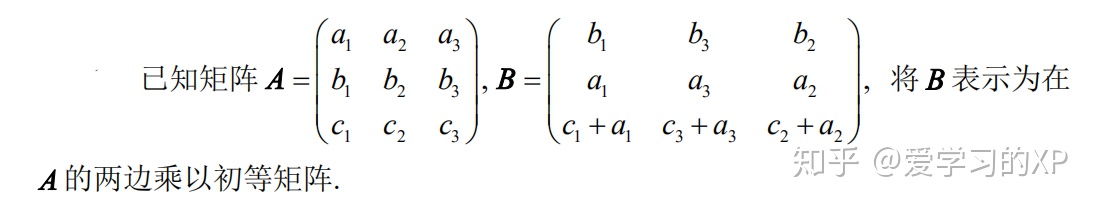
解：
5.求逆矩阵
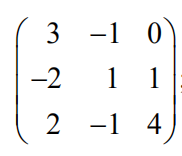
解：
6.利用可逆矩阵求未知矩阵
求满足以下等式的矩阵
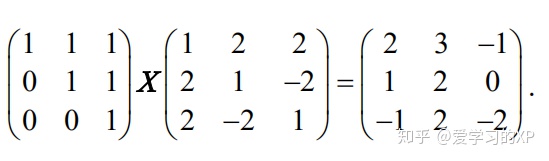
解：
7.利用分块矩阵进行矩阵的三则运算
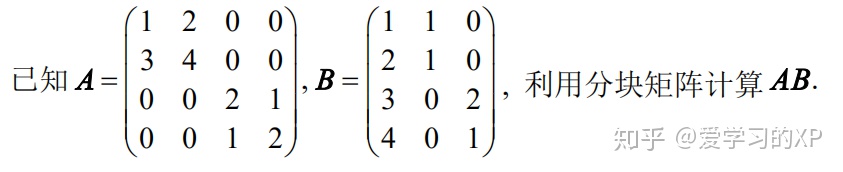
解：
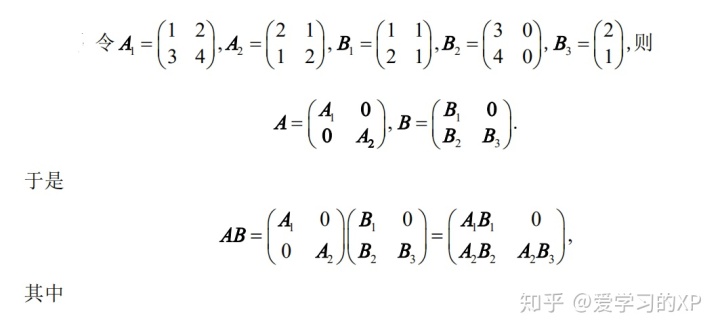
写在后面的话：
知乎码字不易，更多精彩内容以及技巧点拨难以更好的呈现给大家
不过大家可以关注我的公众号，更多精彩内容等你发现
七天期末线性代数急速突破不断更新，期待你的持续关注
喜欢的话点一下赞和关注哦