用三元组实现稀疏矩阵的转置

内容:

设m*n的矩阵中有t个非零元素且t<<m*n,这样的矩阵成为稀疏矩阵，在存储稀疏矩阵时，按照常规方法存储时相当浪费内存，因此提出另外一种存储方法，即只存储非零元素，但在这类矩阵中，通常零元素的排列没有规律，为了能找到相应的元素，仅存储非零元素的值是不够的，还要记下它所在的行和列。于是采取如下办法：将非零元素所在的行、列以及它的值构成一个三元组(i,j,v),然后再按某种规律存储这些三元组，这种方法可以节约存储空间。编写程序用三元组表实现稀疏矩阵的按列转置操作。

步骤：

1. 算法分析

本题需要利用三元组实现稀疏矩阵的按列转置操作。

何为转置操作？所谓矩阵转置，是指变换元素的位置，把位于(row,col)位置上的元素换到(col,row)位置上，也就是说，将元素的行、列互换。

采用三元组表压缩存储稀疏矩阵，实现矩阵的转置时，得到的转置矩阵的三元组表时要按一行一行存放且每行中的元素是按列号从小到大的规律顺序存放，因此在转换时，对a的每一列扫描三元组，找出相应的元素，若找到，则交换其行号与列号，并存储到b的三元组里。

程序中设置了三个函数：

1. 函数InitSPNode()用来建立一个稀疏矩阵的三元组表。首先输入行数、列数和非零元素的值，输入(-1,-1,-1)结束输入。
2. 函数showMatrix()用来输出稀疏矩阵。算法中按矩阵a的列进行循环处理，对a的每一列扫描三元组，找出相应的元素，若找到，则交换其行号和列号，并存储到矩阵b的三元组中。
3. 函数TransposeSMatrix()用来完成稀疏矩阵的转置算法。算法的主要工作是在p和col的两重循环中完成，时间复杂度为O(n*t)。如果非零元素个数t和m*n同数量级，则算法的时间复杂度变为O(m*n^2)。

   2.概要设计

使用C语言，其中设置了以下函数

程序运行流程图如下：

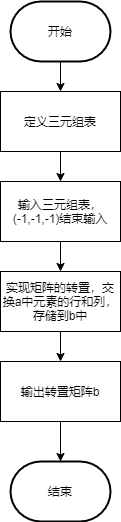
 3.测试

测试样例如下:

 运行结果：

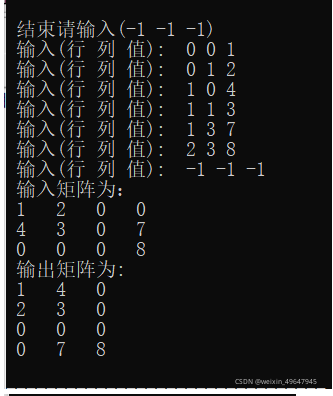
 经测试运行无误。

经过不断的修改和调试，该算法已经基本能够满足要求，对于用户输入的稀疏矩阵，可以方便快捷的完成稀疏矩阵的转置。当非零元素的个数与m*n同数量级时，算法的时间复杂度为O(m*n^2),与传统存储方式下矩阵转置算法相比，节约了一定量的存储空间，但算法的时间性能更差一些，该算法的主要时间耗费在p和col的二重循环上，若能直接确定a中每一个三元组在b中的位置，则对a的三元组表扫描一次即可。算法程序还有待优化。

4.源码如下

#include <stdio.h>
#include <string.h>
#define OK 1
#define Maxsize 10 //用户自定义三元组最大长度
typedef struct { //定义三元组表
	int i,j;
	int v;
}SPNode;
typedef struct
 { //定义三元组表
	SPNode data[Maxsize];
	int m,n,t;//矩阵行、列及三元表长度
}SPMatrix;
void InitSPNode(SPMatrix*a) { //输入三元组表
	int i,j,k,val,maxrow,maxcol;
	maxrow=0;
	maxcol=0;
	i=j=0;
	k=0;
	while(i!=-1&&j!=-1)//row=-1&&col=-1 结束输入
	 { 
		printf(" 输入(行 列 值):  ");
		scanf(" %d %d %d",&i,&j,&val);
		a->data[k].i=i;
		a->data[k].j=j;
		a->data[k].v=val;
		if(maxrow<i) maxrow=i;
		if(maxcol<j) maxcol=j;
		k++;
	}
	a->m=maxrow;
	a->n=maxcol;
	a->t=k-1;
}
void showMatrix(SPMatrix *a) { //输出稀疏矩阵
	int p,q;
	int t=0;
	for(p=0; p<=a->m; p++) {
		for(q=0; q<=a->n; q++) {
			if(a->data[t].i==p&&a->data[t].j==q) {
				printf(" %d  ",a->data[t].v);
				t++;
			} else printf(" 0  ");
		}
		printf("\n"  );
	}
}
void TransposeSMatrix(SPMatrix *a,SPMatrix *b) { //稀疏矩阵转置
	int q,col,p;
	b->m=a->n;
	b->n=a->m;
	b->t=a->t;
	if(b->t) {
		q=0;
		for(col=0; col<=a->n; ++col) //按a的列序转置
			for(p=0; p<a->t; ++p) //扫描整个三元组表
				if(a->data[p].j==col) {
					b->data[q].i=a->data[p].j;
					b->data[q].j=a->data[p].i;
					b->data[q].v=a->data[p].v;
					++q;
				}
	}
}
int main() {
	SPMatrix a,b;
	printf("\n 结束请输入(-1 -1 -1)\n"  );
	InitSPNode(&a);
	printf(" 输入矩阵为：\n" );
	showMatrix(&a);//转置前
	TransposeSMatrix(&a,&b);
	printf(" 输出矩阵为: \n" );
	showMatrix(&b);//转置后
}