概述

FP-growth算法基于Apriori构建，但在完成相同任务时采用了一些不同的技术。这里的任务是将数据集存储在一个特定的称作FP树的结构之后发现频繁项集或者频繁项对，即常在一块出现的元素项的集合FP树。这种做法使得算法的执行速度要快于Apriori，通常性能要好两个数量级以上。
FP-growth算法只需要对数据库进行两次扫描，而Apriori算法对每个潜在的频繁项集都会扫描数据集判定给定模式是否频繁，因此FP-growth算法的速度要比Apiori算法要快。Apriori算法的缺点是多次扫描数据库带来了巨大的IO开销，而FP-growth算法是典型的基于内存的算法，其优点是减少扫描次数来减少IO开销。
FP-growth发现频繁项集的基本过程如下：
(1)构建FP树
(2)从FP树中挖掘频繁项集

FP树的构建

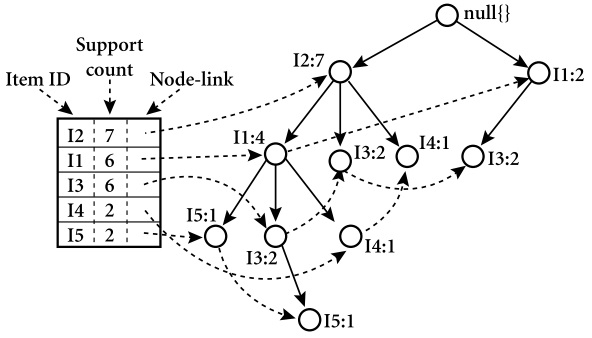
FP树是一种前缀树，有点类似于Trie树但是每个节点有三个指针，分别指向parent，children和nodeLink。此外，算法中还包含有一个头指针表，头指针表中记录每个元素出现的第一个位置（结点），结点中的nodeLink将所有相同的元素连接起来。
第一遍扫描数据库的时候统计每个元素（单项集）出现次数。
第二遍扫描数据库的时候对于原来的每个数据，将数据中支持度小于阈值的元素删除，然后将这个数据按照刚才元素出现次数排序。排序后每个项集都有一个唯一的顺序，这样可以保证后续算法找出所有不重复的频繁项集。然后将这个数据插入到FP树中，并且更新头指针表和nodelink。

挖掘频繁项集

在挖掘频繁项集的时候，类似于Apriori算法，从单项集出发每次增加一个元素。对于每一个频繁项集，我们获得这个频繁项集作为结尾的所有前缀路径（起点为根节点），这些路径的集合称为条件模式基（conditional pattern base）。这里就用到了之前的nodeLink指针，我们可以获得当前所有以某个元素结尾的结点指针。
上面说了，FP-growth类似于Apriori算法，从单项集出发每次增加一个元素。FP-growth算法对于每一个频繁项集以前缀路径构造一棵FP树，然后向当前的频繁项集中添加一个元素，然后以深度优先的策略递归的进行这个过程知道发现所有频繁项集。

例子

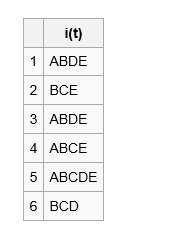
考虑以下数据集

为了构造FP树，首先第一遍扫描数据计算所有单项集的支持度。然后将支持度大于阈值的单项集按照降序排列{ B(6), E(5), A(4), C(4), D(4) }.。
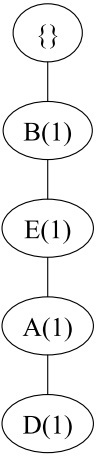
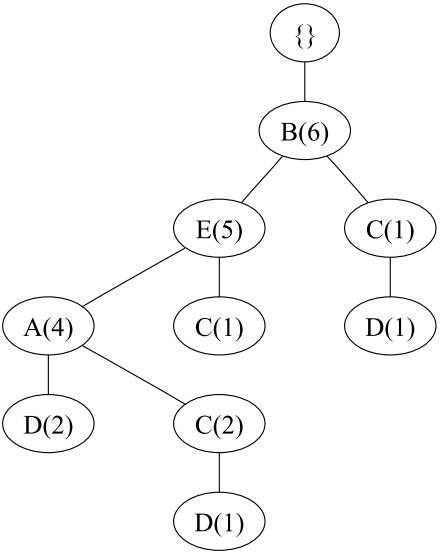
对于第一个数据BEAD，将它插入到FP树中，如下

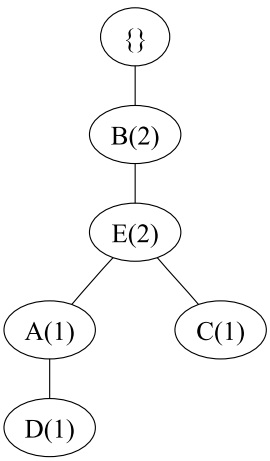
对于第二个数据BEC，插入到FP树中，如下

将剩下的数据做相同的操作，最后得到初始的FP树

然后开始挖掘频繁项集
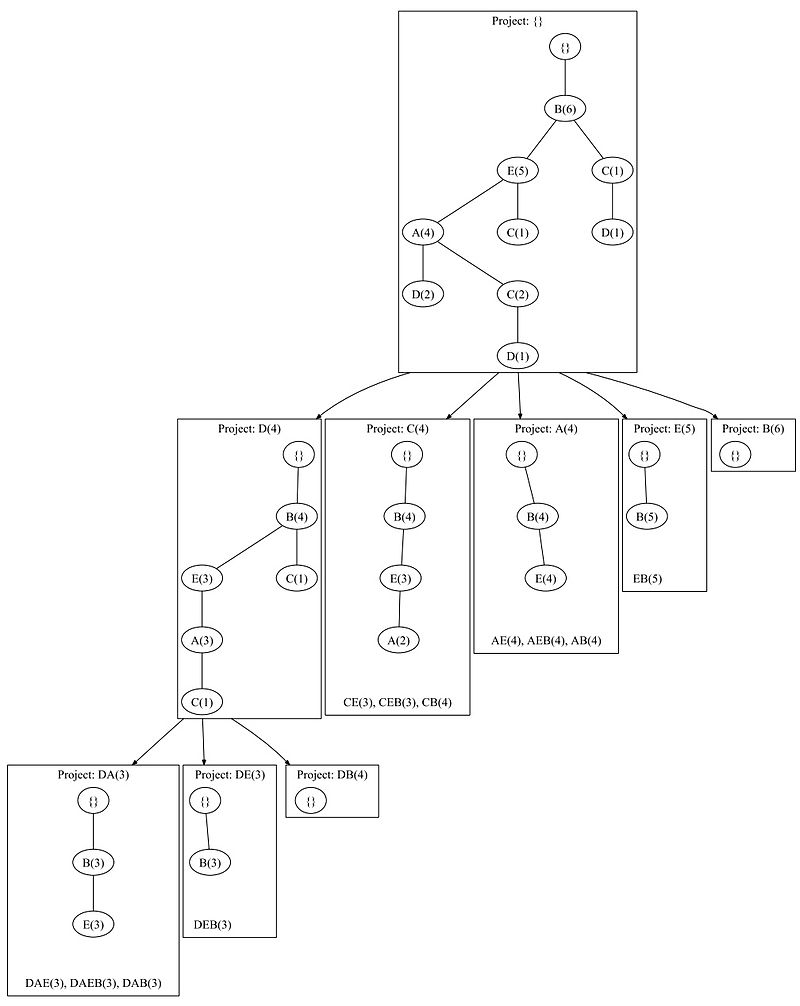
第一次调用的时候利用上面构造的初始树，第一步获得频繁项集{D, C, A, E，B}，用深度优先的策略，以D为后缀的前缀路径构造一棵新的FP树，然后可以得到频繁项集{DA, DE，DB}，然后这样递归下去，直到找到所有频繁项集{ DAE, DAEB, DAB, DEB, CE, CEB, CB, AE, AEB, AB, EB }。流程如下图所示

Python实现代码

from numpy import *


# FP-Growth算法

# 构造数据集
def loadData():
    return [  ['r', 'z', 'h', 'j', 'p'],
              ['z', 'y', 'x', 'w', 'v', 'u', 't', 's'],
              ['z'],
              ['r', 'x', 'n', 'o', 's'],
              ['y', 'r', 'x', 'z', 'q', 't', 'p'],
              ['y', 'z', 'x', 'e', 'q', 's', 't', 'm']]

def createInitSet(dataSet):
    retDic = {}
    for trans in dataSet:
        retDic[frozenset(trans)] = 1
    return retDic

# 定义FP树的结构
class Node:
    def __init__(self, name, count, parent):
        self.name = name
        self.count = count
        self.nodeLink = None
        self.parent = parent
        self.children = {}

    def inc(self, numOccur):
        self.count += numOccur

    def disp(self, ind=1):
        print(' '*ind, self.name, ' ', self.count)
        for child in self.children:
            self.children[child].disp(ind+1)


# 用字典来保存头指针表
def createTree(dataSet, minSup=1):
    headerTable = {}
    for trans in dataSet:
        for item in trans:
            headerTable[item] = headerTable.get(item, 0) + dataSet[trans]
    for i in list(headerTable.keys()):
        if headerTable[i] < minSup:
            headerTable.pop(i)
        else:
            headerTable[i] = [headerTable[i], None]
    if len(headerTable) == 0: return None, None
    retTree = Node('Null Set', 1, None)
    for trans, count in dataSet.items():
        localD = {}
        for item in trans:
            if item in headerTable:
                localD[item] = headerTable[item][0]
        newD = [(v[1], v[0]) for v in localD.items()]
        newD.sort(reverse=True)
        updateTree([v[1] for v in newD], retTree, headerTable, count)
    return retTree, headerTable

# 根据所给的项集更新树
def updateTree(items, node, headerTable, count):
    if len(items) == 0: return
    if items[0] in node.children:
        node.children[items[0]].inc(count)
    else:
        newChild = Node(items[0], count, node)
        node.children[items[0]] = newChild
        if headerTable[items[0]][1] == None:
            headerTable[items[0]][1]  = newChild
        else:
            updateNodeLink(headerTable[items[0]][1], newChild)
    updateTree(items[1:], node.children[items[0]], headerTable, count)

def updateNodeLink(preNode, newNode):
    while preNode.nodeLink != None:
        preNode = preNode.nodeLink
    preNode.nodeLink = newNode

# 寻找前缀路径
def ascendTree(node, path):
    if node.parent != None:
        path.append(node.name)
        ascendTree(node.parent, path)

def findPrefixPath(node):
    condPats = {}
    while node != None:
        prefixPath = []
        ascendTree(node, prefixPath)
        if len(prefixPath) > 1:
            condPats[frozenset(prefixPath[1:])] = node.count
        node = node.nodeLink
    return condPats

def mineTree(node, headerTable, minSup, prefix, freqItemList):
    bigL = [v[0] for v in sorted(headerTable.items(), key=lambda p:p[0])]
    for basePat in bigL:
        newFreqSet = prefix.copy()
        newFreqSet.add(basePat)
        freqItemList.append(newFreqSet)
        condPattBases = findPrefixPath(headerTable[basePat][1])
        newCondTree, newHeaderTable = createTree(condPattBases, minSup)
        if newCondTree != None:
            mineTree(newCondTree, newHeaderTable, minSup, newFreqSet, freqItemList)


simpDat = loadData()
initSet = createInitSet(simpDat)
fpTree, headerTable = createTree(initSet, 3)
#fpTree.disp()
#condPats = findPrefixPath(headerTable['x'][1])
#print(condPats)
freqItems = []
mineTree(fpTree, headerTable, 3, set([]), freqItems)
print(freqItems)