关联分析(Association Analysis)--挖掘啤酒与尿布的关联规则

通过本文我们将了解：

x->y的含义
挖掘关联分析规则的两个步骤
- aproori原理
- 算法优化–剪枝
- 如何生成频繁项集
  - 没有重复的k-项候选集如何产生—>剪枝–>计数–频繁k-项集
关联分析规则的评估指标

什么是关联分析

关联分析是一种简单、实用的分析技术，就是发现存在于大量数据集中的关联性或相关性，从而描述了一个事物中某些属性同时出现的规律和模式。

关联分析是从大量数据中发现项集之间有趣的关联和相关联系。关联分析的一个典型例子是购物篮分析。该过程通过发现顾客放人其购物篮中的不同商品之间的联系，分析顾客的购买习惯。通过了解哪些商品频繁地被顾客同时购买，这种关联的发现可以帮助零售商制定营销策略。其他的应用还包括价目表设计、商品促销、商品的排放和基于购买模式的顾客划分。

可从数据库中关联分析出形如“由于某些事件的发生而引起另外一些事件的发生”之类的规则。

如“67%的顾客在购买啤酒的同时也会购买尿布”，因此通过合理的啤酒和尿布的货架摆放或捆绑销售可提高超市的服务质量和效益。
又如“‘C语言’课程优秀的同学，在学习‘数据结构’时为优秀的可能性达88%”，那么就可以通过强化“C语言”的学习来提高教学效果。

基本概念：

在这里插入图片描述
我们来看上面的事务库，如同上表所示的二维数据集就是一个购物篮事务库。该事物库记录的是顾客购买商品的行为。这里的TID表示一次购买行为的编号，items表示顾客购买了哪些商品。

• 事务（Transaction）
事务库中的每一条记录被称为一笔事务。在上表的购物篮事务中，每一行代表一个事务，每一个商品是一个项，表示一次购物行为。

• 项集（Item Sets）
包含0个或者多个项的集合称为项集。在购物篮事务中，每一样商品就是一个项，一次购买行为包含了多个项，把其中的项组合起来就构成了项集。包含k个项的集合称为k-项集。

• 关联规则（Association Rules）
由集合 X，可以在某置信度下推出集合 Y。关联规则是形如X->Y的蕴含表达式，X称为前件，Y称为后件，X和Y不包含相同的项。即如果 X 发生了，那么 Y 也很有可能会发生。
例如购买了{‘尿布’}的人很可能会购买{‘啤酒’}。关联规则暗示两个物品之间可能存在很强的关系。

• 支持计数（Support count）
项集在事务中出现的次数。例如，｛Bread，Milk｝这个项集在事务库中一共出现了3次，那么它的支持度计数就是3
{Milk,Bread,Diaper｝这个项集在事务库中一共出现了2次，那么它的支持度计数就是2.
记作： $支持度计数：\sigma(\{Milk,Bread,Diaper\})=2$

• 支持度（Support）
指某频繁项集在整个数据集中的比例。假设数据集有 10 条记录，包含{‘啤酒’, ‘尿布’}的有 5 条记录，那么{‘啤酒’, ‘尿布’}的支持度就是 5/10 = 0.5。
又如在上表中共有5个事务，s({Milk,Bread,Diaper})=2/5

对于关联规则的支持度定义为：也就是同时包含X和Y这两个项集的事务占所有事务的比例。即（N是事务个数）：
$s(X\rightarrow Y)=\frac{\sigma (X \cup Y)}{N}$

• 频繁项集（Frequent Item Sets）
如果我们对项目集的支持度设定一个最小阈值（minsup），那么所有支持度大于这个阈值的项集就是频繁项集。

• 置信度（Confidence）
出现某些物品时，另外一些物品必定出现的概率，针对规则而言。
有关联规则如{‘尿布’} -> {‘啤酒’}，那么它的置信度 = 支持度｛尿布，啤酒｝／支持度｛尿布｝**

对于关联规则的置信度定义为：这个定义确定的是Y在包含X的事务中出现的频繁程度。
$c(X\rightarrow Y)=\frac{\sigma (X \cup Y)}{\sigma (X)}$
看｛Bread，Milk｝→{Diaper}这个例子，包含｛Bread，Milk｝项的事务出现了2次，包含｛Bread，Milk，Diaper}的事务也出现了2次，那么这个规则的置信度就是1。

关联规则算法策略

大多数关联规则挖掘算法通常采用的策略是分解为两步

频繁项集的产生，其目标是发现满足具有最小支持度阈值的所有项集，称为频繁项集（frequent itemset）。
规则的产生，其目标是从上一步得到的频繁项集中提取高置信度的规则，称为强规则（strong rule）。通常频繁项集的产生所需的计算远大于规则产生的计算花销。

关联规则发现：

有了上述两个度量，就可以对所有规则做限定，找出对我们有意义的规则。

首先对支持度和置信度分别设置最小阈值minsup和minconf。然后在所有规则中找出支持度≥minsup和置信度≥minconf的所有关联规则。
给定一组事务集合T，关联规则挖掘的目标是查找符合以下条件的所有规则：

支持度 ≥ 支持度最小阈值（support ≥ minsup）
置信度 ≥ 置信度最小阈值（confidence ≥ minconf ）

需要注意的是由简单关联规则得出的推论并不包含因果关系。我们只能由A→B得到A与B有明显同时发生的情况，但不能得出A是因，B是果。

暴力方法：

列出所有可能的关联规则
计算每个规则的支持和置信度
修剪规则，使最小值和最小阈值失败

但是这样做法的计算量令人望而却步！有几种方法可以降低产生频繁项集的计算复杂度。

减少候选项集的数目。如先验(apriori)原理，是一种不用计算支持度而删除某些候选项集的方法。
减少比较次数。利用更高级得到数据结构或者存储候选项集或者压缩数据集来减少比较次数。

我们来做一次分析：
在这里插入图片描述
观察：
上述所有规则都是同一项集的拆分：{Milk, Diaper, Beer} （{牛奶，尿布，啤酒}）
源自同一项集的规则具有相同的支持度（support），但可以有不同的置信度（confidence）
因此，我们可以分离支持度和置信度要求。

再次重申，大多数的关联规则挖掘算法通常采用分解成两步的以下的两个主要子任务的策略：

频繁项集的产生：其目标是发现满足最小支持度阈值的所有项集，这些项集叫做频繁项集（frequent itemset）。
规则的产生：其目标是从上一步发现的频繁项集中提取所有高置信度的规则，这些规则叫做强规则（strong rule）。

通常频繁项集的产生所需的计算远大于规则产生的计算花销。

第一步，频繁项集产生（Frequent Itemset Generation）

格结构常常被用来枚举所有可能的项集，下图显示了 $I=\{a,b,c,d\}$ 的格结构。一般来说，一个包含k个项的数据集可能产生 $2^k-1$ 个频繁项集（不包括空集在内）。由于实际应用中k取值可能非常大，需要探查的项集搜索空间可能是指数规模的。
在这里插入图片描述

有几种方法可以降低产生频繁项集的复杂度：

减少候选项集的数目。如先验(apriori)原理，是一种不用计算支持度而删除某些候选项集的方法。
减少比较次数。利用更高级得到数据结构或者存储候选项集或者压缩数据集来减少比较次数。

先验原理

$先验原理:\,\,\,\,\,\,\,\,\,如果一个项集是频繁的，则它的所有子集一定也是频繁的$

先验原理其实非常好理解：如图
假设{ABC}是频繁的，那么显然{AB}也是频繁的。相反，如果如果{A，B}是非频繁的，那么它的所有超集也是非频繁的。
而一旦发现{AB}是非频繁的，那么包含{AB}的超集可以被立即剪枝（下图灰色部分），这种基于支持度度量修建指数搜索空间的策略叫做 基于支持度的剪枝。
这种剪枝策略依赖于支持度度量的一个关键性质：即一个项集的支持度绝不会超过它的子集的支持度。这个性质也称为支持度度量的反单调性。
在这里插入图片描述

apriori算法的频繁项集产生

下面给出一个实例：
对于下面的事务，假设支持度阈值是60%。即最小支持度计数为3。
在这里插入图片描述
初始时每个项都被看做候选1-项集。对他们进行支持度计数后（下图）。{coke},{Eggs}被丢弃（因为他们出现的次数小于3)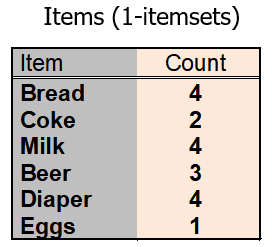

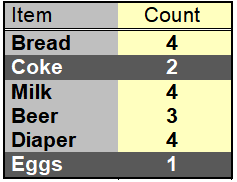
下一次迭代我们仅使用频繁1-项集来生成频繁2-项集。由于只有4个频繁1-项集，所以算法产生的候选2-项集的数目为6（ $C^2_4$ )。
计算完他们的支持度阈值，有4个候选集是非频繁的。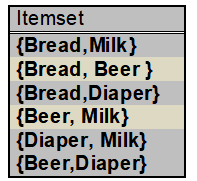
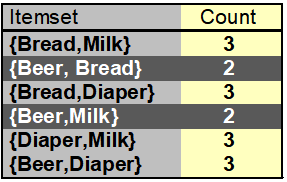
在这里插入图片描述
继续生成3-项集，4个项可生成3（ $C^3_4$ ）个3-项集。
根据先验原理，只保留子集都频繁的3-项集，最后符合的不难看出为{bread，Milk，Diaper}

我们再看暴力做法产生的候选集：（中间的3-候选集个数不难算出为 $C^3_6=20$ ），而枚举所有项集（到3-项集将产生 $C^1_6+C^2_6+C^3_6=41$ 。而使用先验原理减少为6+6+1=13，在这个简单的例子中减少了68%候选集数目。
在这里插入图片描述

关联分析规则的评估指标（Measure for Association Rules）

客观兴趣度量（interestingness Measure)

给定 X ->Y或 {X，Y}，可以从列联表(Contingency table)中获取计算兴趣度量所需的信息
在这里插入图片描述
$f_{11}: support \,of X and Y$
$f_{10}: support \,of X and \bar{Y}$
$f_{01}: support \,of \bar{X} and Y$
$f_{00}: support \,of \bar{X} and \bar{Y}$

举个例子：在这里插入图片描述

关联规则 Tea->Coffee
置信度 $\approx$ P（Coffee|Tea） = 15/20 = 0.75
置信度 > 50%，这意味着喝茶的人更有可能喝咖啡，而不是不喝

看起来规则似乎很合理
一个喝茶的人有75%的可能性会喝咖。
但 P(Coffee)= 0.9，这意味着一个人喝茶会降低一个人喝咖啡的可能性！
请注意，P(Coffee| $\bar{Tea}$ ) = 75/80 = 0.9375

再来看在这里插入图片描述
P（蜂蜜]茶）=50%
confident(Tea→honey)的值不高
但是P（蜂蜜）=12%，所以可以认为喝茶的人更容易点蜂蜜。

上面茶与咖啡的例子中，
P(Coffee|Tea) = 15/20 = 0.75
P(Coffee)= 0.9
Lift = 0.75/0.9 =0.8333 （＜1，因此呈负相关）

主观论据

原文链接：https://blog.csdn.net/weixin_43576422/article/details/106809765