matlab矩阵求伪逆_matlab矩阵及其运算(六)

感谢关注matlab爱好者公众号！如果公众号文章对您有帮助，别忘了点击分享和“在看”哦！若您对公众号有什么意见或建议，请在公众号中回复或在任意文章底部留言！

本文作者：过冷水

广义逆矩阵

   上一期中二狗给大家介绍了广义逆矩阵，并且给出了广义逆矩阵的四种类型，本期二狗带大家对三种常见的广义逆矩阵的求解方法和性质进行讲解。

定义设矩阵为A∈C^mxn如果存在矩阵B∈C^nxm满足。

(1)ABA=A

(2)BAB=B

(3)(AB)^H=AB

(4)(BA)^H=BA

     H:表示共轭转置

的一部分或者全部，则称B为A的广义逆矩阵

由定义可知，广义逆矩阵共有

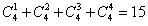
即有十五种广义逆矩阵.matlab矩阵及其运算(五)连载中给出了四种实际案例，有兴趣的可以自行回顾学习。

(1)  只满足：ABA=A类型的广逆矩阵记为A^-

(2)  只满足：ABA=A、BAB=B类型的广逆矩阵称为自反广逆矩阵，记做A_r^-

(3)  满足全部方程的广义逆矩阵称为伪逆矩阵记做A⁺

A^-

定理一：设A∈C^mxn,则A满足方程

AA^-A=A

的广义逆矩阵A^-存在的充要条件为对于任何b∈R(A),A^-b都是方程组。

AX=b

的一个解，其中R(A)为A的列空间。

证:设 A=(a₁,a₂,...a_n),其中a_i为A的第i列，i∈n,若存在矩阵A^-,使得b∈R(A),A^-b都为方程组的解，则应由AA^-b=b对所有b∈R(A)成立，特别应有

AA-a_i=a_i

故有

AA^-(a₁,a₂,...a_n)=(a₁,a₂,...a_n)

即AA^-A=A

反之，设存在A^-，使得AA^-A=A，由于对于任何b∈R(A)，必存在X∈C^mxn,使

AX=b

对AA^-A=A两边同时右乘X，得

AA^-AX=AX

由式AX=b可得

AA^-b=b

故A^-b是方程组AX=b的一个解。

定理二：任给A∈C_r^mxn,总有M∈C_m^mxn,P∈C_n^nxn,使得

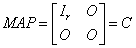
且

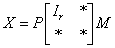
注：*表示任意数

是A满足ABA=A的广义逆矩阵A^-

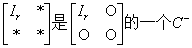
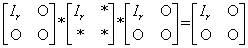
证

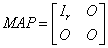
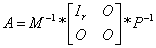
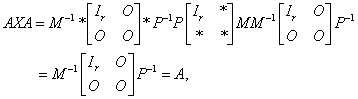
故

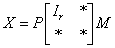
案例：已知A求一个广义逆矩阵A^-

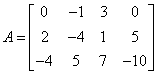
解：求M∈C_m^mxn,P∈C_n^nxn,使得

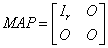
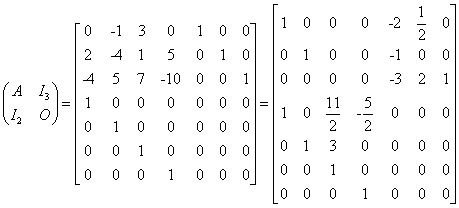
可得

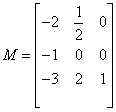
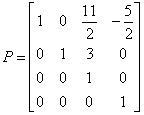
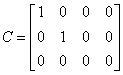
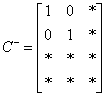
则

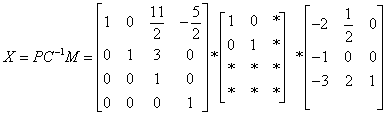
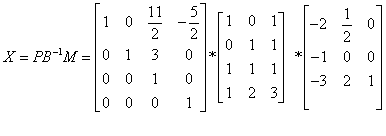
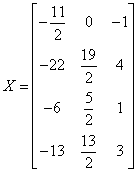
即为一个广义逆矩阵A^-.

定理三：设A∈C_r^mxn,λ∈C，则

(1)(A^T)^-=(A^-)^T,(A^H)^-=(A^-)^H;

(2)若R(A)=m=n,则A^-=A^-1;

(3)λ⁺A^-是λA的广义逆矩阵，其中

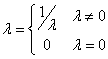
(4)若S∈C_m^mxm,T∈C_n^nxn,B=SAT,则T^-1A^-S^-1是B的广义逆矩阵；

(5)AA^-则A^-A均为幂等矩阵，且R(A)=R(AA^-)=R(A^-A);

对本篇连载能够看进去且看懂的读者可以自证定理三，在公众号或者文末进行留言回复，可查看证明过程。

A_r^-

当A∈C_m^mxn,若存在矩阵B∈C_n^nxm,使得

ABA=A,BAB=B

则称B为A的自反广义逆矩阵，记作A_r^-即B=A_r^-,这时A与B互为自反广义逆矩阵

定理一：设A∈C_m^mxn,X,Y∈C_n^nxm,且X,Y均为A的广义逆矩阵，则

AXA=A,AYA=A,

Z=XAY

为A的自反广义逆矩阵。

证：因为

AZA=AXAYA=(AXA)YA=AYA=A

ZAZ=(XAY)A(XAY)=X(AYA)(XAY)=X(AXA)Y=Z

故Z=XAY为A的自反广义逆矩阵，该定理给出了A_r^-一种具体构造方法。

案例

已知A求一个广义逆矩阵A^-

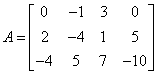
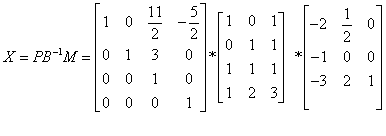
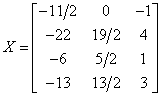
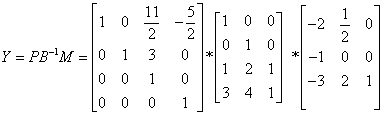
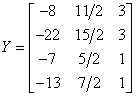
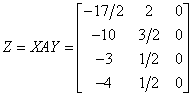
定理二：设A^-∈C^nxm,则A∈C^mxn的广义逆矩阵，则A^-是A的自发广义逆矩阵的充要条件为

R(A^-)=R(A)

证 充分性 设AA^-A=A,且R(A^-)=R(A)，于是由R(A^-A)=R(A^-)及

R(A^-)=R(A)=R(AA^-A)≤R(A^-A)≤R(A^-)

有

R(A^-A)=R(A^-)

所以存在X^-∈C^nxm,使得

A-=A^-AX

且

A=A^-AA=(AAA)XA=AXA

故X也是A的广义逆矩阵，故可知A^-是A的自反广义逆矩阵。

必要性 设A^-是A的自反广义逆矩阵，则

AA^-A=A,    A^-AA^-=A^-

由此可得

R(A)≤R(A^-),   R(A^-)≤ R(A)

证明完毕

定理三：设X∈C^nxm,A∈C^mxn,则

(1)R(A)≤R(X);(2)AXA=A;(3)XAX=X

中任两条成立，可推出第三条成立。

读者可自证，证明过程可通过公众号留言，和大家分享。

定理四：设A∈C^mxn,则

Y=(A^H*A)^-*A^H,       Z=A^H*(A*A^H)^-

均为A的自反广义逆矩阵。

证：由于对任意的A∈C^mxn,总有

R(A^H)=R(A^HA),

故总存在矩阵D∈C^nxm,使得

A^H=A^HAD

所以

AYA=D^HA^HAYA=D^H(A^HA)(A^HA)^-(A^HA)=D^HA^HA=A

所以Y为A的广义逆矩阵。

又由于

R(Y)=R(A^HA)^-A^H≤R(A^H)=R(A)

由定理三可知Y为A的自反广义逆矩阵。同理可证Z也是A的自反广义逆矩阵。

A⁺

伪逆矩阵是广逆矩阵中的一种。

定义：设A∈C^mxn,X∈C^nxm,若同时有

(1)ABA=A

(2)BAB=B

(3)(AB)^T=AB

(4)(BA)^T=BA

则称X为A的伪逆矩阵，记做A⁺,即X=A⁺

定理一：若A∈C^mxn，且A=BC是A的最大秩分解，则

X=C^H(CC^H)^-1(B^HB)^-1B^H

是A的伪逆矩阵。

证      

AXA=BCC^H(CC^H)^-1(B^HB)^-1B^HBC=BC=A

XAX=C^H(CC^H)^-1(B^HB)^-1B^HBCC^H(CC^H)^-1(B^HB)^-1B^H=X

(AX)^H=[BCC^H(CC^H)^-1(B^HB)^-1B^H]^H=[B(B^HB)^-1B^H]^H

=B(B^HB)^-1B^H=AX

(XA)^H=[C^H(CC^H)^-1(B^HB)^-1B^HBC]^H=[C^H(CC^H)^-1C]^H

=C^H(CC^H)^-1C=XA

该定理给出了伪逆矩阵的存在性和具体求法。

定理二：伪逆矩阵唯一。

证 设X,Y均为A的伪逆矩阵，则

X=XAX=XAYAX=X(AY)^H(AX)^H=XY^HA^HX^HA^H=XY^HA^H

=X(AY)^H=XAY=(XA)^HY=A^HX^HY=A^HY^HA^HX^HY

=(YA)^H(XA)^HY=YAXAY=YAY=Y

即

X=Y

定理三：设A∈C^mxn，则

(1)(A^T)⁺=(A⁺)^T,(A^H)^-+=(A⁺)^H;

(2)(A⁺)⁺=A;

(3)A⁺=(A^HA)⁺A^H=A^H(AA^H)⁺;

(4)R(A⁺)=R(A^H).

感兴趣的读者可以自证并留言查看证明过程。

定理四：设A∈C^mxn，A=BC为A的最大秩分解，则

A⁺=C⁺B⁺ 

伪逆矩阵求解案列：设

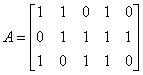
求其伪逆矩阵A⁺

解首先对A进行最大秩分解，由于

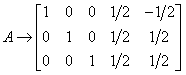
所以A的最大秩分解为

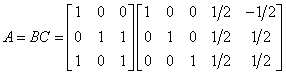
已知 A⁺=C⁺B⁺

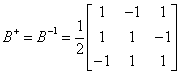
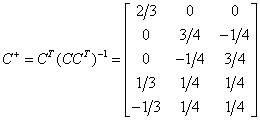
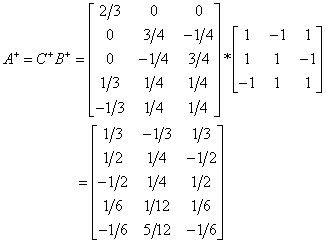
   本期关于广逆矩阵的类型及其性质就介绍完毕，下期会给大家讲讲广逆矩阵的实际应用，对矩阵感兴趣的请持续关注matlab矩阵及其运算连载。

方阵求逆代码

function  X=Ni(A)%Input  - A is an N x N matrix%Output - I is an N x N inverse matrix of A %and I(j,:)containing the solution to AX(:,j) =E(:,j).%Initialize X, Y,the temporary storage matrix C, and the row % permutation information matrix R[N,N]=size(A);B=eye(N);   %B is an N x N identity matrixX=zeros(N,N);Y=zeros(N,N);C=zeros(1,N);R=1:N;%the next steps is to find the factorization(factorize for only once)for p=1:N-1%Find the pivot row for column p   [max1, j]=max(abs(A(p:N,p)));%Interchange row p and j      C=A(p,:);      A(p,:)=A(j+p-1,:);      A(j+p-1,:)=C;      d=R(p);      R(p)=R(j+p-1);      R(j+p-1)=d;      if A(p,p)==0      'A is singular.  No unique solution'      break      end   %Calculate multiplier and place in subdiagonal portion of A      for k=p+1:N         mult=A(k,p)/A(p,p);     A(k,p) = mult;         A(k,p+1:N)=A(k,p+1:N)-mult*A(p,p+1:N);      endendfor j=1:N        %when j is fixed then the method is similar to the Program 3.3    %Solve for Y(:,j)    Y(1,j) = B(R(1),j);    for k=2:N        Y(k,j)= B(R(k),j)-A(k,1:k-1)*Y(1:k-1,j);    end    %Solve for X(:,j)    X(N,j)=Y(N,j)/A(N,N);    for k=N-1:-1:1        X(k,j)=(Y(k,j)-A(k,k+1:N)*X(k+1:N,j))/A(k,k);    endend

  伪逆矩阵代码

function  Y=PNi(A)Y=A*Ni(A*A')end

自反逆矩阵代码  

function  Y=PPNi(A)format ratm=rref(A)/Ap=(rref((rref(A))')/rref(A)')'c=m*A*p;Y=p*c'*m;end

往期推荐：

图论碎碎念(1)

图论与渡河问题

蒙特卡洛法应用

matlab矩阵及其运算(五)

matlab演奏《雨碎江南》