目录
深度优先基础概念总结
1.深度优先代码模板(二叉树为例)
def dfs(node):
if node in visited:
#already visited
return
visited.add(node)
#process current node
#logic here
dfs(node.left)
dfs(node.right)2.符合我们递归思维的深度优先代码模板(多叉树为例)
visited = set()
def dfs(node,visited):
if node in visited:
#terminator # already visited
return
visited.add(node)
#process current node here
for next_node in node.children:
if not next_node in visited:
dfs(next_node,visited)
题目一:岛屿数量
(题目链接:https://leetcode-cn.com/problems/number-of-islands/)
给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
示例 1:
输入:grid = [
["1","1","1","1","0"],
["1","1","0","1","0"],
["1","1","0","0","0"],
["0","0","0","0","0"]
]
输出:1
思路:采用沉岛法活着说是水冲法:遍历整个二维网格,当发现是‘1’的话,就把1自己和它相邻的陆地全部变为0
如何把相邻的也变为0了?采用深度优先进行递归。递归终止条件:要么是超出二维网格范围,要么是遇到水。
**:最终岛屿的数量就是我们两重for遍历二维网格过程中进行深度优先搜索的次数
class Solution {
public int numIslands(char[][] grid) {
if(grid == null ||grid.length ==0){
return 0;
}
int num_island = 0;
int reslut = 0;
int x_length = grid.length;
int y_length = grid[0].length;
for(int r=0;r<x_length;r++){
for(int c = 0;c<y_length;c++){
if(grid[r][c] == '1'){
num_island+=1;
dfs_sink(grid,r,c);
}
}
}
return num_island;
}
public void dfs_sink(char[][] grid, int r,int c){
if(r< 0||r>=grid.length||c<0||c>=grid[0].length||grid[r][c]=='0'){
return;
}
grid[r][c]='0';
dfs_sink(grid,r+1,c);
dfs_sink(grid,r,c+1);
dfs_sink(grid,r-1,c);
dfs_sink(grid,r,c-1);
}
}[注意]:终止条件:if(r< 0||r>=grid.length||c<0||c>=grid[0].length||grid[r][c]=='0') 别忘了grid[r][c] == '0'.
题目二:水域大小
(题目链接:https://leetcode-cn.com/problems/pond-sizes-lcci/)你有一个用于表示一片土地的整数矩阵land,
该矩阵中每个点的值代表对应地点的海拔高度。若值为0则表示水域。
由垂直、水平或对角连接的水域为池塘。池塘的大小是指相连接的水域的个数。
编写一个方法来计算矩阵中所有池塘的大小,返回值需要从小到大排序。
示例:
输入:
[
[0,2,1,0],
[0,1,0,1],
[1,1,0,1],
[0,1,0,1]
]
输出: [1,2,4]
思路:采用与题目一中类似的沉岛/水冲法。采用两个for遍历整个二维网格,当遇到水域即0是调用深度优先搜索其周围的相邻水域,把相邻水域全部变为陆地
**:最终两重for循环中调用深度优先搜索的次数就是我们水域的数量。
至于水域面积的计算,就在我们深度优先搜索函数中去实现,每次遇到0面积就加1
【注意】:Java值传递有两种,一种是值传递,一种是引用对象传递,
我们计算面积的时候,函数中的面积是动态变化的,我们要使用引用对象传递,
所以在函数参数里面我们使用了list对象的大小来保存面积
返回面积之后我们先存储起来最后再进行排序放在数组结果里面
class Solution {
public int[] pondSizes(int[][] land) {
List<Integer> res = new ArrayList<Integer>();
int num_island = 0;
for(int l=0;l<land.length;l++){
for(int c = 0; c<land[0].length;c++){
if(land[l][c]==0){
num_island+=1;
int currarea=dfs_sink(land,l,c,new ArrayList<>());
res.add(currarea);
//System.out.println(currarea);
}
}
}
Collections.sort(res);
int[] finalresult = new int[res.size()];
for (int i = 0; i < res.size(); i++) {
finalresult[i] = res.get(i);
}
return finalresult;
}
public int dfs_sink(int[][] land,int l,int c,List<Integer> area){
if( l<0 || l>= land.length || c<0 || c>=land[0].length || land[l][c]>=1){
return area.size();
}
land[l][c] = 1;
area.add(l);
// 检验面积
dfs_sink(land,l-1,c,area);
dfs_sink(land,l+1,c,area);
dfs_sink(land,l,c-1,area);
dfs_sink(land,l,c+1,area);
dfs_sink(land,l-1,c-1,area);
dfs_sink(land,l-1,c+1,area);
dfs_sink(land,l+1,c+1,area);
dfs_sink(land,l+1,c-1,area);
return area.size();
}
}[注意]:我亲自用变量int进行传参,发现是不对的,我们必须用引用对象进行传参,才能保证结果正确。
此时用ArrayList的效果就显现出来了。而且主函数中传入的ArrayList必须是新的,即每次传入的是new ArrayList<Integer>().
题目三:求根到叶子结点数字之和
(题目链接:https://leetcode-cn.com/problems/sum-root-to-leaf-numbers/)
给定一个二叉树,它的每个结点都存放一个 0-9 的数字,每条从根到叶子节点的路径都代表一个数字。
例如,从根到叶子节点路径 1->2->3 代表数字 123。
计算从根到叶子节点生成的所有数字之和。
说明: 叶子节点是指没有子节点的节点。
示例 1:
输入: [1,2,3]
1
/ \
2 3
输出: 25
解释:
从根到叶子节点路径 1->2 代表数字 12.
从根到叶子节点路径 1->3 代表数字 13.
因此,数字总和 = 12 + 13 = 25.
思路:这道题我们不要被题目要求牵着鼻子走,如果我们要把每条路径上
代表的数字求出来再相加,这样需要一直记录,并且不太好处理。
我们的方法:路径上面每个结点都对应一个数字,而每个结点对应的数字等于
其父亲结点对应的数字乘以10加上自身结点对应的数字之和
所以代码中我们使用
int sum = presum*10+root,val
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int sumNumbers(TreeNode root) {
return dfs(root,0);
}
public int dfs(TreeNode root, int presum){
if(root == null){
return 0;
}
int sum = presum*10+root.val;
if(root.left ==null && root.right == null){
return sum;
}else{
return dfs(root.left,sum)+dfs(root.right,sum);
}
}
}题目四:二叉树的所有路径
给定一个二叉树,返回所有从根节点到叶子节点的路径。
说明: 叶子节点是指没有子节点的节点。
示例:
输入:
1
/ \
2 3
\
5
输出: ["1->2->5", "1->3"]
解释: 所有根节点到叶子节点的路径为: 1->2->5, 1->3
思路:采用dfs,注意递归结束条件:当遇到空结点递归停止
注意一条路径结束条件:左结点和右结点同时为空,即学会
if(root.left == null && root.right == null)的使用。
方法二:也可以直接用if(root !=null)一直把结点加入到路径中
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
List<String> res = new ArrayList<String>();
public List<String> binaryTreePaths(TreeNode root) {
dfs(root,"");
return res;
}
public void dfs(TreeNode root,String currpath) {
if(root == null){
return;
}
if(root.left==null && root.right ==null){
currpath += root.val;
res.add(new String(currpath));
//System.out.println(res);
}
currpath += root.val;
//System.out.println(currpath);
currpath += "->";
//System.out.println(currpath);
dfs(root.left,currpath);
dfs(root.right,currpath);
}
}[注意]:学会if(root==null)和if(root.left==null && root.right == null)的配合使用。
题目五:二叉树的最小深度
(题目链接:https://leetcode-cn.com/problems/minimum-depth-of-binary-tree/)
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明:叶子节点是指没有子节点的节点。
示例 1:
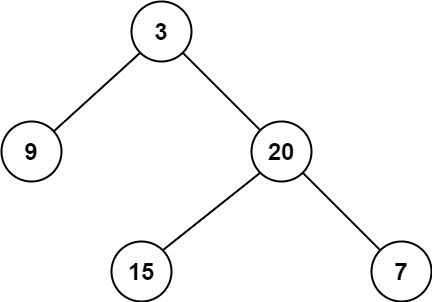
输入:root = [3,9,20,null,null,15,7]
输出:2
示例 2:
输入:root = [2,null,3,null,4,null,5,null,6]
输出:5
思路:本题的主要难点:理解题目所说的叶子结点的意思,只有当某结点的左结点,右结点同时为空的时候,
该结点才算叶子结点。
如果某个结点一侧为空,一侧不为空,那么返回当前深度即可Math.max(l,r)
class Solution {
public int minDepth(TreeNode root) {
if(root==null){
return 0;
}
else{
return dfs(root);
}
}
public int dfs(TreeNode root){
if(root == null){
return 0;
}
int l = dfs(root.left);
int r = dfs(root.right);
if(root.left==null || root.right ==null){
return Math.max(l,r)+1;
}else{
return Math.min(l,r)+1;
}
}
}方法二:把所有路径找出来,再把最短的求出来即可。
方法三:深度优先,遍历整棵树,记录最小深度
对于每个非叶子节点,我们只需要分别计算其左右子树的最小叶子节点的深度。
class Solution {
public int minDepth(TreeNode root) {
if(root == null) return 0;
int minvalue = Integer.MAX_VALUE;
if(root.left == null && root.right == null){
return 1;
}
if(root.left != null){
minvalue = Math.min(minDepth(root.left), minvalue);
}
if(root.right != null){
minvalue = Math.min(minDepth(root.right), minvalue);
}
return minvalue+1;
}
}