图论—最短路

Dijkstra算法

Floyd算法

例题

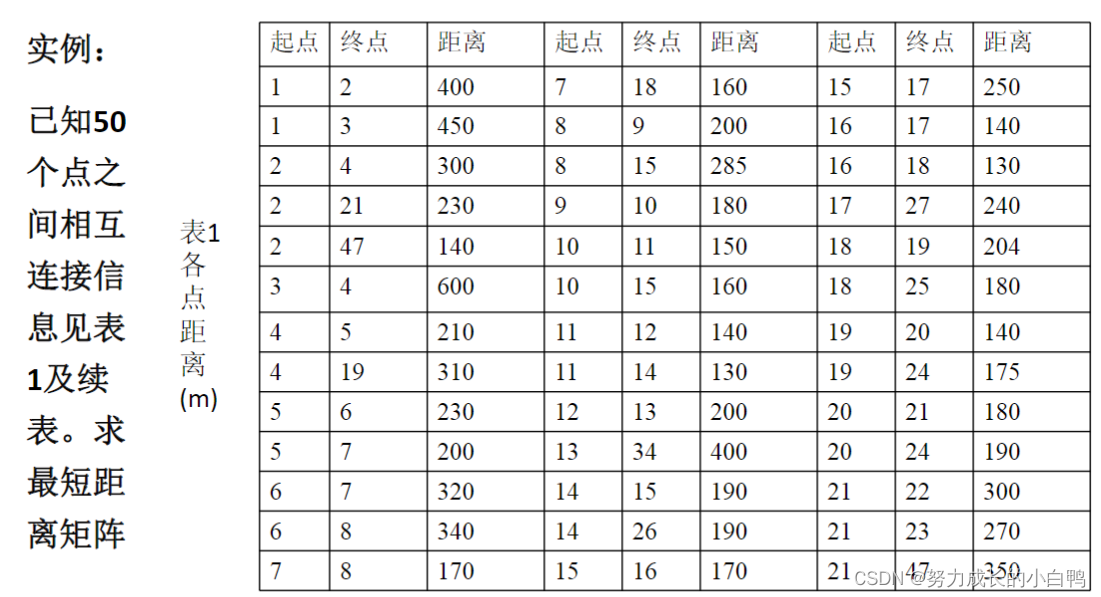
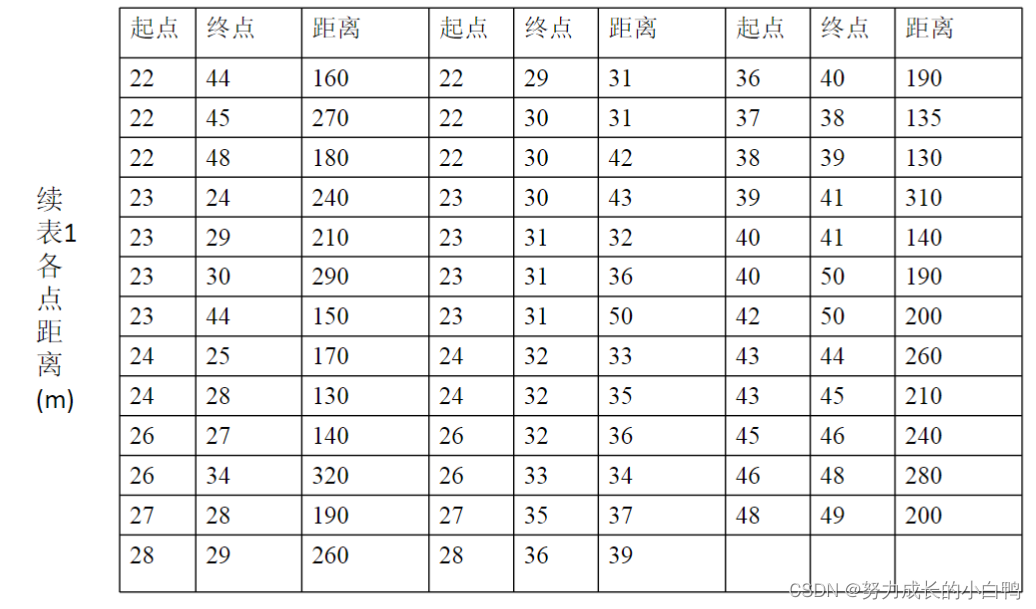
Matlab代码实现如图

%floyd算法
n=50;
A=zeros(n,n);
%初始化矩阵
for i=1:n
    for j=1:n
        if(i==j)
            A(i,j)=0;
        else
            A(i,j)=10000;
        end
    end
end
A(1,2)=400;A(1,3)=450;A(2,4)=300;A(2,21)=230;A(2,47)=140;A(3,4)=600;A(4,5)=210;A(4,19)=310;A(5,6)=230;A(5,7)=200;A(6,7)=320;
A(6,8)=340;A(7,8)=170;A(7,18)=160;A(8,9)=200;A(8,15)=285;A(9,10)=180;A(10,11)=150;A(10,15)=160;A(11,12)=140;A(11,14)=130;
A(12,13)=200;A(13,34)=400;A(14,15)=190;A(14,26)=190;A(15,16)=170;A(15,17)=250;A(16,17)=140;A(16,18)=130;A(17,27)=240;A(18,19)=204;
A(18,25)=180;A(19,20)=140;A(19,24)=175;A(20,21)=180;A(20,24)=190;A(21,22)=300;A(21,23)=270;A(21,47)=350;A(22,44)=160;A(22,45)=270;
A(22,48)=180;A(23,24)=240;A(23,29)=210;A(23,30)=290;A(23,44)=150;A(24,45)=170;A(24,28)=130;A(26,27)=140;A(26,34)=320;A(27,28)=190;
A(28,29)=260;A(22,29)=31;A(22,30)=31;A(22,30)=42;A(23,30)=43;A(23,31)=32;A(23,31)=36;A(23,31)=50;A(24,32)=33;A(24,32)=35;A(26,32)=36;
A(26,33)=34;A(27,35)=37;A(28,36)=39;A(36,40)=190;A(37,38)=135;A(38,39)=130;A(39,41)=310;A(40,41)=140;A(40,50)=190;A(42,50)=200;
A(43,44)=260;A(43,45)=210;A(45,46)=240;A(46,48)=280;A(48,49)=200;
for j=1:n
    for i=1:j-1
        A(j,i)=A(i,j);  %使矩阵对称
    end
end
B=A;
%利用Floyd算法计算最短距离矩阵
for k=1:n
    for i=1:n
        for j=1:n
            t=B(i,k)+B(k,j);
            if t<B(i,j)
                B(i,j)=t;
            end
        end
    end
end
%输出距离矩阵到文件
fid=fopen('disrance.txt','w');
for i=1:n
    for j=1:n
        fprintf(fid,'%4d',B(i,j));
    end
    fprintf(fid,'\n');
end
fclose(fid);
                

部分结果如下