
大纲:
- 常见的离散型概率分布(二项,几何,超几何,泊松)
- 常见的连续型概率分布(指数,正态,均匀)
- 三大抽样分布(卡方,t,F)
- 一些推论和分布之间的关系
离散型分布
- 二项分布
实验重复n次,每次实验相互独立(伯努利实验),实验有两种结果,成功概率p,失败概率1-p。
在二项分布中,我们关注的是在n次试验中成功的次数(区别于几何分布)。
举个栗子:
当我们要计算抛硬币n次,恰巧有x次正面朝上的概率,可以使用二项分布的公式:
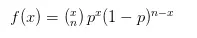
二项概率的数学期望为E(x) = np,方差D(x) = np(1-p)。
- 几何分布
几何分布(英语:Geometric distribution)指的是以下两种离散型概率分布中的一种:
- 在伯努利试验中,得到一次成功所需要的试验次数 X
- 在得到第一次成功之前所经历的失败次数 X
n重伯努利实验
在第X次成功的概率:
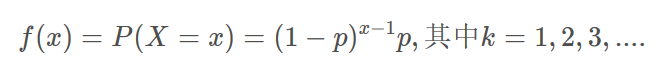
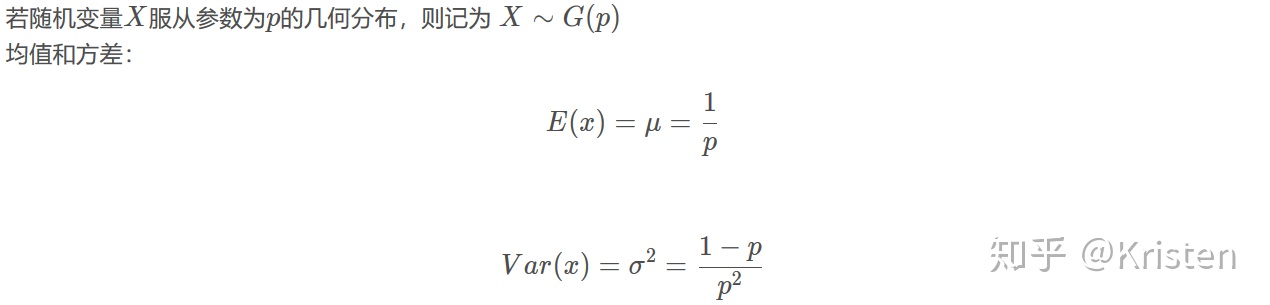
- 超几何分布
超几何分布是统计学上一种离散概率分布。它描述了由有限个物件中抽出n个物件,成功抽出指定种类的物件的个数(不归还 (without replacement))。
例如:从N个样本中抽取n个,N个中有r个不合格的,求抽到x个不合格样本的概率。
超几何分布的概率分布,均值和方差:
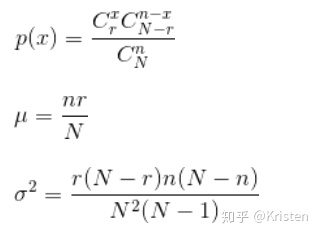
- 泊松分布
泊松概率的成立条件是在任意两个长度相等的时间区间中,事件发生的概率是相同的,并且事件是否发生都是相互独立的。
x代表发生x次,u代表发生次数的数学期望,概率函数为:
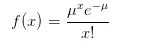
实际计算过程中用这个公式更好理解:
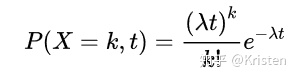
t是你要计算的时间区间长度,t=1时即为泊松分布(单位时间),扩展后的函数是泊松过程。
泊松分布的数学期望和方差相等,因此E(x) = D(x) = λ。
连续型分布
- 均匀分布
在取值区间内出现概率相同(常数)
概率密度函数,均值和方差:

- 指数分布
指数分布是连续型概率分布!!!放在这里是因为它跟泊松分布关系密切,可以由泊松分布推导而来。
指数分布是事件的时间间隔的概率。时间间隔大于t,等同于t时间内事件次数为0的概率,而后者的概率可以由泊松过程给出。
推导过程:
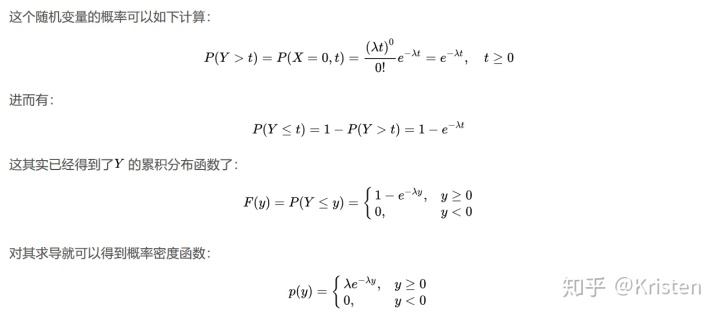
指数分布的期望和方差:若以λ为参数,则是E(X)=1/λ D(X)=1/λ²
- 正态分布

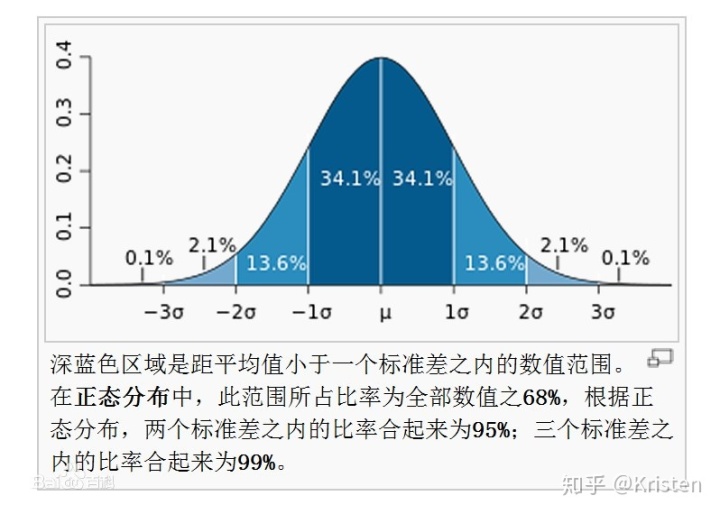
正态分布的经验法则:
均值±标准差:68.3%
均值±2标准差:95.4%
均值±3标准差:99.7%
抽样分布
- 点估计和区间估计
点估计:用样本统计量估计总体参数,未给出估计的可靠程度(置信度)
区间估计:给定置信水平,以估计值为中心给出真实值可能出现的区间范围。
- 大数定律和中心极限定理
大数定律:样本量趋近于无穷时,样本均值收敛到总体期望
中心极限定理:
1,样本均值约等于总体均值
2,抽样次数趋近于无穷时,样本均值围绕总体均值呈现正态分布(无论总体分布是否服从正态分布)
- 标准差与标准误
标准差 = 一次抽样中个体分数间的离散程度,反映了个体分数对样本均值的代表性,用于描述统计
标准误 = 多次抽样中样本均值间的离散程度,反映了样本均值对总体均值的代表性,用于推论统计
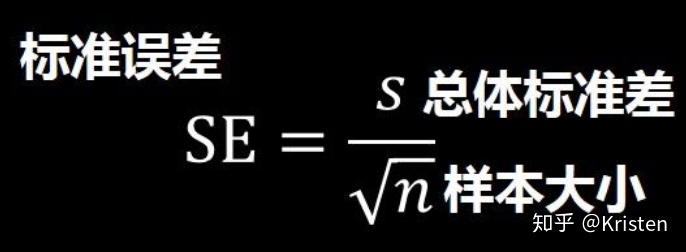
- 卡方分布

概率密度函数及其形状:
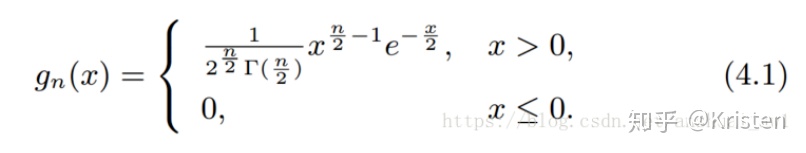
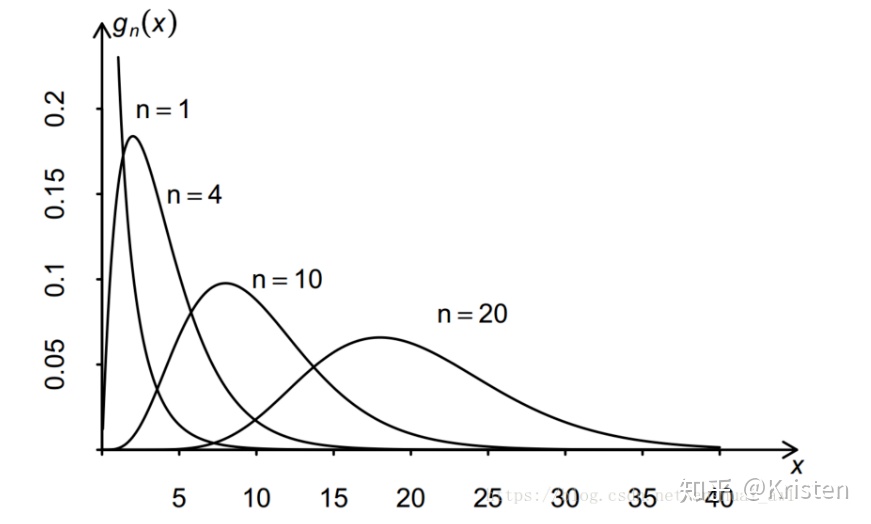
当自由度n增大时,卡方分布的概率密度函数趋于对称。
卡方分布的性质:

- t分布
在讲t分布之前先了解下t检验和z检验:
- Z-Test 用于大样本(n>30),或总体方差已知;
- T-Test 在小样本(n<30),且总体方差未知时,适用性优于Z-Test,而在大样本时,T-Test 与 Z-Test 结论趋同。
单样本t统计量:由于总体标准差未知,一般用样本标准差S估计总体标准差

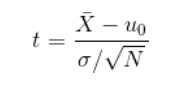
双样本t统计量:

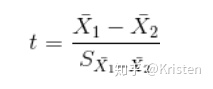
t统计量的分布服从t分布。当样本量无限大时,t分布无限接近于正态分布N(0,1)。
自由度为n的t分布

概率密度函数及其形状:
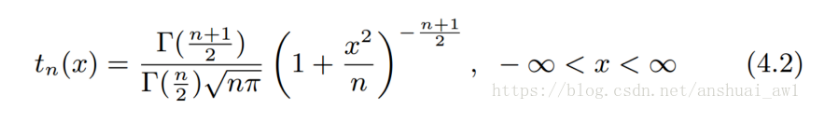
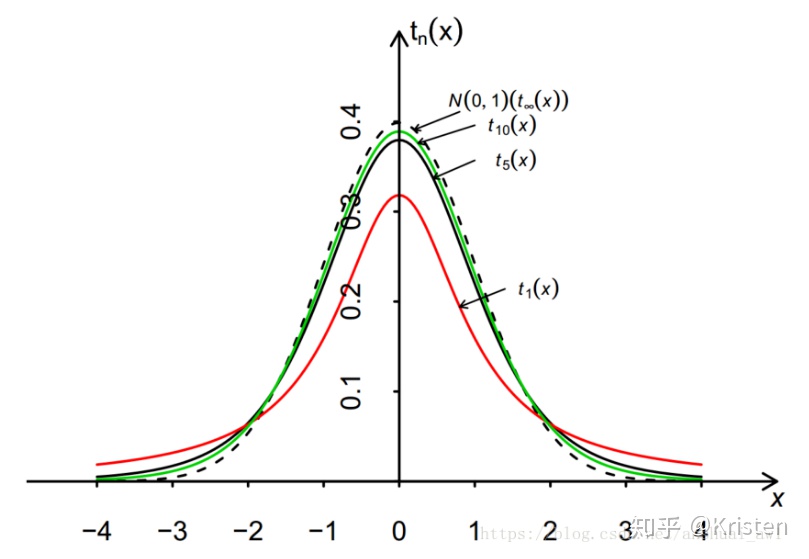
t变量的性质:当n趋向于无穷大时,t变量的极限分布为N(0,1)。
- F分布

概率密度函数及其图形:
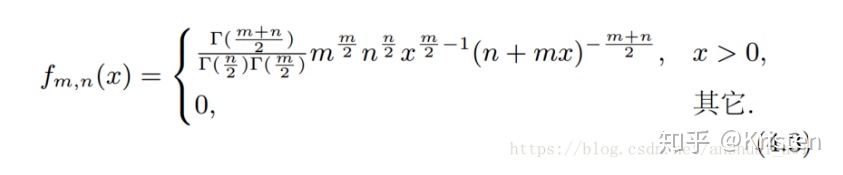
自由度为m,n的F分布的密度函数
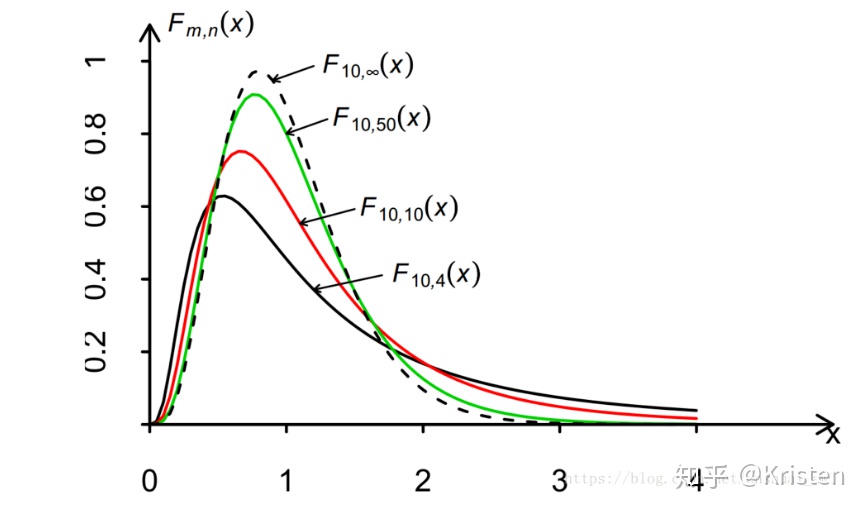
F分布的自由度m和n是有顺序的, 当m≠n时, 若将自由度m和n的顺序颠倒一下, 得到的是两个不同的F分布.
F变量的性质:
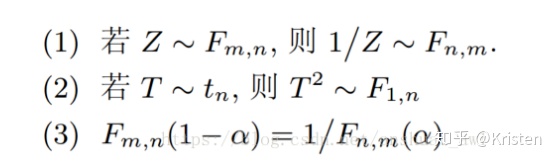
几个重要推论和分布间的关系
- 正态变量线性函数的分布
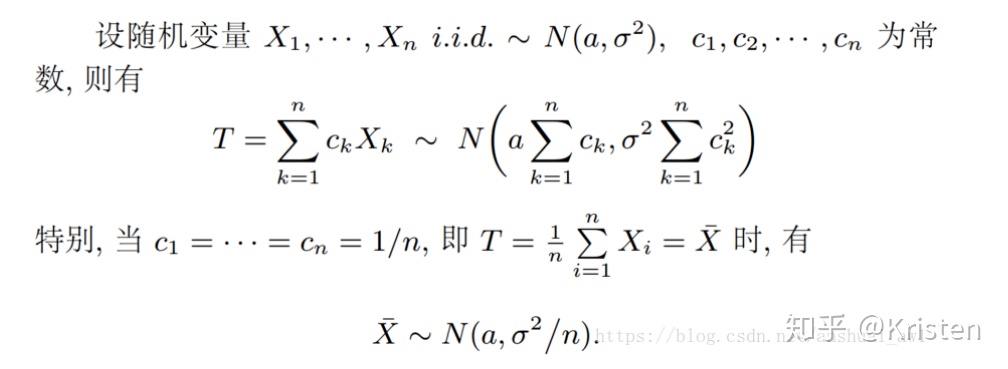
- 正态变量样本均值和样本方差的分布

- 一些推论
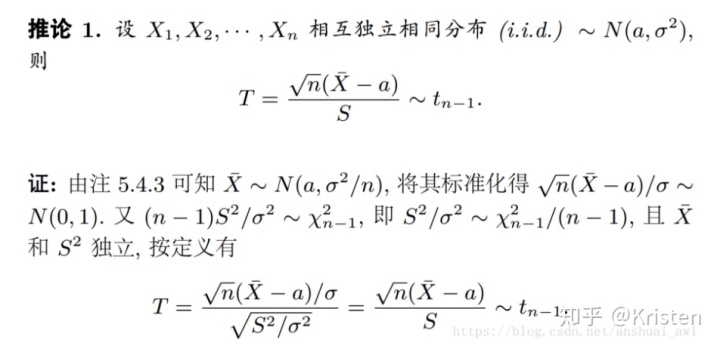
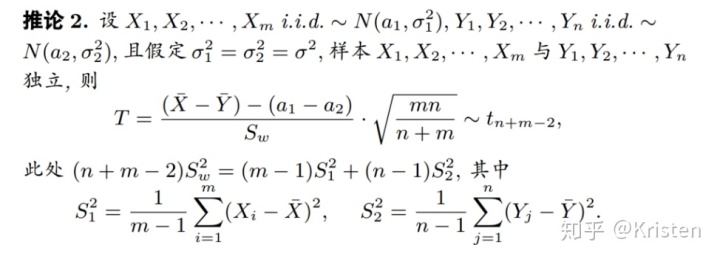



参考资料:
小白都能看懂的95%置信区间_bitcarmanlee的博客-CSDN博客
https://blog.csdn.net/anshuai_aw1/article/details/82656691
《商务与经济统计》学习笔记(七)-各统计分布知识点归纳_天阑之蓝的博客-CSDN博客
如何七周成为数据分析师15:读了本文,你就懂了概率分布 | 人人都是产品经理