openfoam学习心得—RANS模型k、ε \varepsilonε、ω \omegaω输运方程
1. 动量、质量守恒方程
在一个实际工程中,湍流是不可预测的,即使边界上很小的扰动都可能产生截然不同的流场,这在数学上表现为N-S方程的混沌现象,为了解决这一问题,就产生了所谓的系综平均法—也就是RANS模型,其求得的是在实验中所有可能情况的平均,这样的见解好像在国内的教材上没有出现过,让不少人以为RANS模型仅仅是为了降低DNS的计算量,我起初也是如此,知道看到了《Turbulent Flows》-Pope这本书,如理解有偏差,还请dalao们不吝赐教!
不可压缩流体中用来预测平均场的方程(RANS)和原始的N-S方程相差不大:
2. 雷诺应力
从上面可以看到,差别仅仅是在偏应力之一项上,τ R \tau ^{R}τR便是我们所说的雷诺应力,根据Boussinesq假设,将雷诺应力张量假设成与牛顿流体一样的形式–也就是各项同性应力+各项异性应力+体积膨胀应力,如下: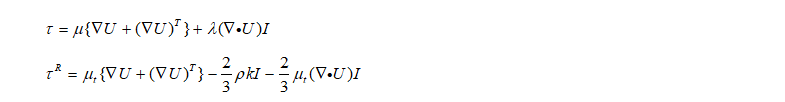 不可压缩流体的散度为0,并且把各项同性应力并入到p中,方程也就变为:
不可压缩流体的散度为0,并且把各项同性应力并入到p中,方程也就变为: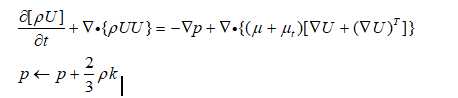
也就是说一点的应力(学过弹性力学的都知道一点有9个应力分量,知道了这九个应力分量就可以计算出一点沿着任何方向的截面上的力,进而推出等效体力的公式面力等效体力公式)(包括各向同性与各项异性应力)由两块组成-雷诺应力与粘性应力
接下来只要能够确定涡粘性系数μ t \mu_{t}μt,一切就迎刃而解了。μ t \mu_{t}μt是一个与U,P一样的一个变量,而不是常数。
3. k方程
k是湍动能,是个标量,如同一般的变量的标量运输方程一样,拥有时间导数项,对流项、扩散项,从大尺度湍流中得到能量,也就是湍动能产生项Pk,能量会在小尺度脉动中耗散(都对应的是单位体积能量的产生与耗散),也就是 ε \varepsilonε,其张量形式及展开形式如下,其等式左端复合求导展开去除质量守恒,也能化为非守恒型方程:
由于不可压缩流体密度为常数且散度为0,带有k的项可以消掉,最终湍动能产生项Pk就是各种速度梯度的乘积之和,具体形式可参考《数值传热学》-陶文铨P350。

4. ε \varepsilonε方程
ε \varepsilonε方程没有引入新的量,推倒完上面之后,每一项都比较清晰,如下:)
就算完 k与ε \varepsilonε之后,根据一个代数方程就可以计算出涡粘性系数μ t \mu_{t}μt,从而闭合方程组。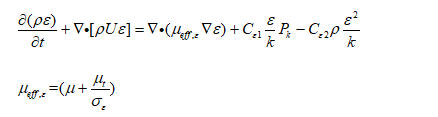
5. ω \omegaω方程
k-ω \omegaω方程有多种形式,ω \omegaω被认为是单位体积单位时间湍动能转换为内能的速率,the well-known k-ω \omegaω is reported by Wilcox,如下,与之前的方程形式大同小异: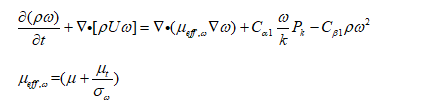
笔者疫情期间被困在家,实在不想手推公式,但观万物后总结才能提高,遂借此方式克服惰性,下一篇学习壁面函数在CFD中如何实施-拜读大神的知乎文https://zhuanlan.zhihu.com/p/32520364 (:orz