题目传送门
A. Marketing Scheme
题意
- 一个准备买 x 个物品,他一次可以一包物品有 a 个打折更便宜,
- 他首先先回卖 x/a 包整包的物品,
- 之后对剩余的 s = x% a 报物品如果,s>=a/2 那么他就会在买一包 a,否则他只会零卖 s 个物品,
- 现在一个顾客准备卖 l~r 个物品,怎么安排 a 的大小可以使这个顾客的总是卖的比他准备的卖的多?
思路
- 首先如果 a >=l && a <= r 这个时候顾客肯定不会多买,
- 否则的话的我们考虑 a>r, 这样 l 和 r 都小于 a,一定存在 r >= a/2 && l >= a / 2, 当我们考虑如果 l >= a / 2 成立的时候 r >= a / 2 一定成立,
- 所以我们只需要考虑 2l >= a 就行了,又因为 a>r, 所以 2l>r 的时候就可以选择出一个符合题意的 a,输出 yes
- 否则输出 no
- 如果 a<r 的时候,我也不会,只能借用别人的题解中的回答:

代码
#include <iostream>
#include <stdio.h>
#include <string.h>
#include <math.h>
#include <algorithm>
#include <string>
#include <string>
#include <map>
#include <bitset>
#include <vector>
void fre() { system("clear"), freopen("A.txt", "r", stdin); freopen("Ans.txt","w",stdout); }
void Fre() { system("clear"), freopen("A.txt", "r", stdin);}
void Run(int x = 0) {
#ifdef ACM //宏定义免注释 freopen
if(! x) fre(); else Fre();
#endif
}
#define ios ios::sync_with_stdio(false)
#define Pi acos(-1)
#define pb push_back
#define fi first
#define se second
#define db double
#define ll long long
#define ull unsigned long long
#define Pir pair<ll, ll>
#define m_p make_pair
#define for_(i, s, e) for(ll i = (ll)(s); i <= (ll)(e); i ++)
#define rep_(i, e, s) for(ll i = (ll)(e); i >= (ll)(s); i --)
#define memset(a, b, c) memset(a, (int)b, c);
#define size() size() * 1LL
#define sc scanf
#define pr printf
#define sd(a) scanf("%lld", &a)
#define ss(a) scanf("%s", a)
#define inf 0x3f3f3f3f
#define INF 0x3f3f3f3f3f3f3f3f
#define esp 1e-7
#define mod (ll)(1e9 + 7)
using namespace std;
/*=========================ACMer===========================*/
const ll mxn = 2e5 + 10;
int main()
{
Run();
ll T; sd(T);
while(T --)
{
ll a, b;
sc("%lld %lld", &a, &b);
if(a * 2 > b)
pr("YES\n");
else
pr("NO\n");
}
return 0;
}
B. Reverse Binary Strings
题意
- 这题给我们一个长度为 n 的 01 字符串且 0 和元素的数量均为 n/2(n 为偶数),对于任意一次操作我们可以翻转一个子区间,问我们最少需要几次操作使所有的 01 串中的相同的元素不相邻。
思路
这题盲猜的答案:max (所有 1 子串的总长度 - 所有 1 子串的个数,所有 0 子串的总长度 - 0 子串的个数)
代码
#include <iostream>
#include <stdio.h>
#include <string.h>
#include <math.h>
#include <algorithm>
#include <string>
#include <string>
#include <map>
#include <bitset>
#include <vector>
void fre() { system("clear"), freopen("A.txt", "r", stdin); freopen("Ans.txt","w",stdout); }
void Fre() { system("clear"), freopen("A.txt", "r", stdin);}
void Run(int x = 0) {
#ifdef ACM //宏定义免注释 freopen
if(! x) fre(); else Fre();
#endif
}
#define ios ios::sync_with_stdio(false)
#define Pi acos(-1)
#define pb push_back
#define fi first
#define se second
#define db double
#define ll long long
#define ull unsigned long long
#define Pir pair<ll, ll>
#define m_p make_pair
#define for_(i, s, e) for(ll i = (ll)(s); i <= (ll)(e); i ++)
#define rep_(i, e, s) for(ll i = (ll)(e); i >= (ll)(s); i --)
#define memset(a, b, c) memset(a, (int)b, c);
#define size() size() * 1LL
#define sc scanf
#define pr printf
#define sd(a) scanf("%lld", &a)
#define ss(a) scanf("%s", a)
#define inf 0x3f3f3f3f
#define INF 0x3f3f3f3f3f3f3f3f
#define esp 1e-7
#define mod (ll)(1e9 + 7)
using namespace std;
/*=========================ACMer===========================*/
const ll mxn = 2e5 + 10;
char s[mxn];
int main()
{
Run();
ll T; sd(T);
while(T --)
{
ll n; sd(n);
ss(s + 1);
if(s[n] == '0')
s[n + 1] = '1';
else
s[n + 1] = '0';
ll ans = 0, t = 0;
for_(i, 1, n + 1)
{
if(s[i] == '0')
{
ans += max(t, 0LL);
t = 0;
continue;
}
if(s[i] == s[i - 1])
t ++;
}
ll res = 0;
t = 0;
for_(i, 1, n + 1)
{
if(s[i] == '1')
{
res += max(t, 0LL);
t = 0;
continue;
}
if(s[i] == s[i - 1])
t ++;
}
pr("%lld\n", max(ans, res));
}
return 0;
}
C. Chef Monocarp
题意
- 给我们 n 个物品,每个物品有个时间属性 t,表示把这个件物品取出来的最合适的时间,现在把 n 个物品放到一个盒子中,在 x 分钟的时候去第 i 讲物品的事的花费为:∣ x − t i ∣ |x - t_i|∣x−ti∣,
- 每分钟只能取出一个物品,
- 问把所有物品都去除来的时候最小花费是多少。
思路
- 动态规划,dp [i][j] 表示在第 i 件物品在第 j 分钟的时候的花费,
- 状态转移方程为:dp [i][j]=min (dp [i][j],dp [i-1][k]+ | j - t_i | ) (其中:k>=1&&k<j)
代码
#include <iostream>
#include <stdio.h>
#include <string.h>
#include <math.h>
#include <algorithm>
#include <string>
#include <string>
#include <map>
#include <bitset>
#include <vector>
void fre() { system("clear"), freopen("A.txt", "r", stdin); freopen("Ans.txt","w",stdout); }
void Fre() { system("clear"), freopen("A.txt", "r", stdin);}
void Run(int x = 0) {
#ifdef ACM //宏定义免注释 freopen
if(! x) fre(); else Fre();
#endif
}
#define ios ios::sync_with_stdio(false)
#define Pi acos(-1)
#define pb push_back
#define fi first
#define se second
#define db double
#define ll long long
#define ull unsigned long long
#define Pir pair<ll, ll>
#define m_p make_pair
#define for_(i, s, e) for(ll i = (ll)(s); i <= (ll)(e); i ++)
#define rep_(i, e, s) for(ll i = (ll)(e); i >= (ll)(s); i --)
#define memset(a, b, c) memset(a, (int)b, c);
#define size() size() * 1LL
#define sc scanf
#define pr printf
#define sd(a) scanf("%lld", &a)
#define ss(a) scanf("%s", a)
#define inf 0x3f3f3f3f
#define INF 0x3f3f3f3f3f3f3f3f
#define esp 1e-7
#define mod (ll)(1e9 + 7)
using namespace std;
/*=========================ACMer===========================*/
const ll mxn = 2e5 + 10;
ll ar[mxn];
ll dp[205][405];
int main()
{
Run();
ll T; sd(T);
while(T --)
{
ll n; sd(n);
for_(i, 1, n) sd(ar[i]);
sort(ar + 1, ar + 1 + n);
ll t = 2 * n;
memset(dp, INF, sizeof dp);
for_(i, 1, t) dp[1][i] = abs(ar[1] - i);
for_(i, 2, n)
{
for_(j, 1, t)
{
for_(k, 1, j - 1)
{
dp[i][j] = min(dp[i][j], dp[i - 1][k] + abs(ar[i] - j));
}
}
}
ll ans = INF;
for_(i, 1, t)
{
ans = min(ans, dp[n][i]);
}
pr("%lld\n", ans);
}
return 0;
}
D. Minimal Height Tree(模拟、构造)
题意
- 给我们一个 bfs 遍历序列(层序遍历,如下图),让我们构造出一个以 1 为根节点的最小高度的树(对这个树跑 bfs 的时候得出的序列就是给我们的序列),而且知道这个数的所有子节点的标号依次增大。
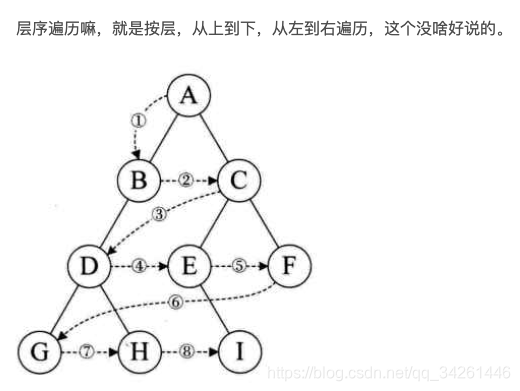
思路
- 其实有了层续遍历这个概念,其实这一题是比较好做的,
- 思路就是,我尽量个将每个升序的子序列接到树的目前的根结点处,并且该子序列的长度即为下次可以接的子树的个数量。
代码
#include <iostream>
#include <stdio.h>
#include <string.h>
#include <math.h>
#include <algorithm>
#include <string>
#include <string>
#include <map>
#include <bitset>
#include <vector>
void fre() { system("clear"), freopen("A.txt", "r", stdin); freopen("Ans.txt","w",stdout); }
void Fre() { system("clear"), freopen("A.txt", "r", stdin);}
void Run(int x = 0) {
#ifdef ACM //宏定义免注释 freopen
if(! x) fre(); else Fre();
#endif
}
#define ios ios::sync_with_stdio(false)
#define Pi acos(-1)
#define pb push_back
#define fi first
#define se second
#define db double
#define ll long long
#define ull unsigned long long
#define Pir pair<ll, ll>
#define m_p make_pair
#define for_(i, s, e) for(ll i = (ll)(s); i <= (ll)(e); i ++)
#define rep_(i, e, s) for(ll i = (ll)(e); i >= (ll)(s); i --)
#define memset(a, b, c) memset(a, (int)b, c);
#define size() size() * 1LL
#define sc scanf
#define pr printf
#define sd(a) scanf("%lld", &a)
#define ss(a) scanf("%s", a)
#define inf 0x3f3f3f3f
#define INF 0x3f3f3f3f3f3f3f3f
#define esp 1e-7
#define mod (ll)(1e9 + 7)
using namespace std;
/*=========================ACMer===========================*/
const ll mxn = 2e5 + 10;
ll ar[mxn];
int main()
{
Run();
ll T; sd(T);
while(T --)
{
ll n; sd(n);
ll ans = 1, sum = 1;
ll cnt = 0, now = 0;
sd(ar[1]);
for_(i, 2, n)
{
sd(ar[i]);
if(ar[i] > ar[i - 1])
now ++;
else
{
cnt ++;
if(cnt == sum)
{
ans ++;
cnt = 0;
sum = now;
}
}
}
pr("%lld\n", ans);
}
return 0;
}
版权声明:本文为qq_34261446原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。