非线性优化-高斯牛顿法

实践slam中介绍的高斯牛顿法，其实非线性优化是门独立的课程，在很多领域都有应用，如机械优化设计、数值分析，最近再回顾一遍。

前言

slam中将求状态估计问题转化为求最大似然估计的问题，接着又将最大似然估计问题转为最小二乘问题。由于函数是非线性函数，这个最小二乘问题可以用优化的思路来求解。其中，高斯牛顿法，就是一种经典的求解优化问题的方法。在刘惟信教授主编的《机械最优化设计》，高斯牛顿法又被叫做最小二乘法。优化问题，最重要的两点就是方向和步长，搞清楚这两点，就抓住了问题的主要矛盾。每次前进一点点，目标函数的值就下降一点，当步长变化很小的时候，再也没法前进时候，就到达了最小值（当然也可能陷入局部的最小值）。

一、什么是高斯-牛顿法？

1.概念

高斯-牛顿法是用去求解无约束问题的优化方法，一般用于求函数平方和的极小值问题，且不必计算二阶偏导数矩阵，收敛速度较快。

当遇到目标函数为：
$$F(X)=\sum _{i=1}^m{f}_i^2(X)X\in E^n(m\ge n)$$可以Gauss-Newteon求解$F(X)$的极小值，不必计算二阶偏导数，而计算一阶偏导数即可求解。若是求解一般的优化问题，需要将目标函数转为平方和的形式。

因为
$$\frac{\partial F(X)}{\partial x_j}=2\sum _{i=1}^m{f}_i(X)\frac{\partial f_i(X)}{\partial x_j}(j=1,2,...,n)$$
展开可写为：
$$\begin{array}{rl}▽F(X)=& \left[\begin{array}{c}\frac{\partial F(X)}{\partial x_1}\\ \frac{\partial F(X)}{\partial x_2}\\ ⋮\\ \frac{\partial F(X)}{\partial x_n}\end{array}\right]=2\left[\begin{array}{c}{\sum }_{i=1}^m{f}_i(X)\frac{\partial f_i(X)}{\partial x_1}\\ {\sum }_{i=1}^m{f}_i(X)\frac{\partial f_i(X)}{\partial x_2}\\ ⋮\\ {\sum }_{i=1}^m{f}_i(X)\frac{\partial f_i(X)}{\partial x_n}\end{array}\right]\\ =& 2\left[\begin{array}{cccc}\frac{\partial f_1(X)}{\partial x_1}& \frac{\partial f_2(X)}{\partial x_1}& \cdots & \frac{\partial f_m(X)}{\partial x_1}\\ \frac{\partial f_1(X)}{\partial x_2}& \frac{\partial f_2(X)}{\partial x_2}& \cdots & \frac{\partial f_m(X)}{\partial x_2}\\ ⋮& ⋮& ⋮& ⋮\\ \frac{\partial f_1(X)}{\partial x_n}& \frac{\partial f_2(X)}{\partial x_n}& \cdots & \frac{\partial f_m(X)}{\partial x_n}\end{array}\right]\left[\begin{array}{c}{f}_1(X)\\ f_2(X)\\ ⋮\\ f_m(X)\end{array}\right]\\ =& 2J(X{)}^{T}f(X)...(1)\end{array}$$

其中，$J(X)=[J_{ij}(X){]}_{m\times n}$ 为Jacobian matrix，$J_{i,j}=\frac{\partial f_i(X)}{\partial x_j}，i=1,...,m;j=1,...,n$。

将$f_i(X)在X=X^{(k)}处用Taylor展开近似为$：
$$f_i(X)\approx f_i(X^{(k)})+[▽f_i(X^k)][X-X^{(k)}]=l_i^k(X)$$

$$F(X)=\sum _{i=1}^m{f}_i^2(X)=\sum _{i=1}^m[l_i^k(X)]=L^k(X)$$
则$$\frac{{\partial }^{2}F(X)}{\partial x_i\partial x_j}\approx \frac{{\partial }^2{L}^k(X)}{\partial x_i\partial x_j}=2▽f_i(X^k)▽f_j(X^k)=2\sum _{i=1}^m{J}_{ri}(X^k)J_{rj}(X^k)$$
$${▽}^{2}F(X^k)\approx 2[J(X^k){]}^{T}J(X^k)...(2)$$
将（1）、（2）代入到牛顿法的公式当中
$$X^{(k+1)}=X^k-H(X^k{)}^{-1}▽F(X^k)$$
得$$X^{(k+1)}=X^k-[J(X^k{)}^{T}J(X^k){]}^{-1}J(X^k{)}^{T}f(X)$$
从这也可以看出为什么Guass_Newton法叫做最小二乘法。

将求逆这项放到左边，可得：
$$[J(X^k{)}^{T}J(X^k)]△X=J(X^k{)}^{T}f(X)$$
类似$Ax=b$，是一个典型的最小二乘问题，也可以看出$A$的性质对求解方程非常关键。

因此步长为$△X=J(X^k{)}^{T}f(X)$，方向为$-[J(X^k{)}^{T}J(X^k){]}^{-1}$。

视觉SLAM十四讲中的推导更简单明了一点。如果增量矩阵$H(X^k{)}^{-1}$不可逆，将导致算法不收敛。

2.算法流程

这里给出的是修正Gauss-Newton法的流程。

1. 给定初始点$X^{(0)}$和收敛精度$\epsilon$
2. 令k=0，求当前的雅可比矩阵$J(X^{(k)})$
3. 求步长$S^{(k)}=-[J(X^{(k)}{)}^{T}J(X^{(k)}){]}^{-1}J(X^{(k)}{)}^{T}f(X)$
4. 进行一维探索求最优步长${\alpha }^{(k)}$，求新点$X^{(k+1)}=X^{(k)}+{\alpha }^{(k)}{S}^{(k)}$
   使得$minF(X^{(k)}+\alpha S^{(k)})=F(X^{(k)}+{\alpha }^{(k)}{S}^{(k)})$
5. 若$||X^{(k+1)}-X^{(k)}||⩽\epsilon$，则停止计算，否则回到2

二、代码案例

1.问题描述

假设带拟合的曲线方程形式为：
$$y=\exp (a{x}^2+bx+c)$$
用$y=\exp (a{x}^2+bx+c)+w$，引入高斯噪声来生成N个观测的数据点，根据这些点求曲线的参数$a，b，c$。

那么，该问题转化求解下面的优化目标
$$minF(X)=min\frac{1}{2}\sum _{i=1}^N||y_i-\exp (a{x}_i^2+b{x}_i+c)|{|}^2$$
优化变量为$a，b，c$。

3.代码实现

代码如下：

#include <iostream>
#include <opencv2/opencv.hpp>
#include <chrono>
#include <Eigen/Core>
#include <Eigen/Dense>

using namespace std;
using namespace Eigen;

int main(){
	double ar=1.0, br=2.0, cr=1.0;//真实参数值
	double ae=2.0, be=-1.0,ce=6.0;//估计参数值
	int N=100;
	double w_sigma=1.0;			  //噪声干扰值
	double inv_sigma=1.0/w_sigma;
	cv::RNG rng;
	
	//生成数据点，用两个向量来存储
	vector<double> x_data, y_data;
	for(int i=0;i<N;i++){
		double x=i/100.0;
		x_data.push_back(x);
		y_data.push_back(exp(ar*x*x+br*x+cr)+rng.gaussian(w_sigma*w_sigma));	
	}
	
	//Gauss_Newton迭代
	int iterations = 100;//最大迭代次数
	double cost = 0, lastcost = 0;
	chrono::steady_clock::time_point start_t1 = chrono::steady_clock::now();
	for(int i;i<iterations;i++){
		//初始化海森矩阵
		Matrix3d H = Matrix3d::Zero();
		Vector3d b = Vector3d::Zero();
		cost = 0;
		//每迭代一次要计算100个点
		for(int j=0;j<N;j++){
			double xi = x_data[j],yi = y_data[j];
			double error = yi - exp(ae*xi*xi+be*xi+ce);
			Vector3d J;
			//初始化雅可比矩阵
			J[0] = -xi*xi*exp(ae*xi*xi+be*xi+ce);
			J[1] = -xi*exp(ae*xi*xi+be*xi+ce);
			J[2] = -exp(ae*xi*xi+be*xi+ce);
		H += J*J.transpose();//3*3
		b += -error*J;		//代码定义的J为列向量，公式中定义为行向量
		cost += error*error;//目标函数值
		}
		
		//求步长，通过解线形方程Hx=b
		Vector3d dx = H.ldlt().solve(b);//LDLT分解方法
		if (isnan(dx[0])){
			cout << "result is nan!" << endl;
			break;
		}
		
		//如果目标函数不再减小就停止
		if(i>0 && cost >=lastcost)
		{
			cout << "cost: " << cost << ">=last cost: " << lastcost << ", break." << endl;
			break;
		}
		//更新变量，上一时刻的值+变量
		ae += dx[0];
		be += dx[1];
		ce += dx[2];
		lastcost = cost;
		cout << "total cost: "<<cost<<", \t\t update: "<<dx.transpose()<<
		"\t\t estimated params: "<< ae<<","<<be<<","<<ce<<endl;
	}
	chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
	chrono::duration<double> time_used = chrono::duration_cast<chrono::duration<double>>(t2-t1);
	cout<<"solve time cost = "<< time_used.count() << " seconds. "<<endl;
	cout<<"estimated abc = "<< ae << ", " <<be << ", " << ce <<endl;
	return 0;
}

结果如下，每次运行消耗的时间会有一定的差异，大约在9ms左右，其实并不是很快。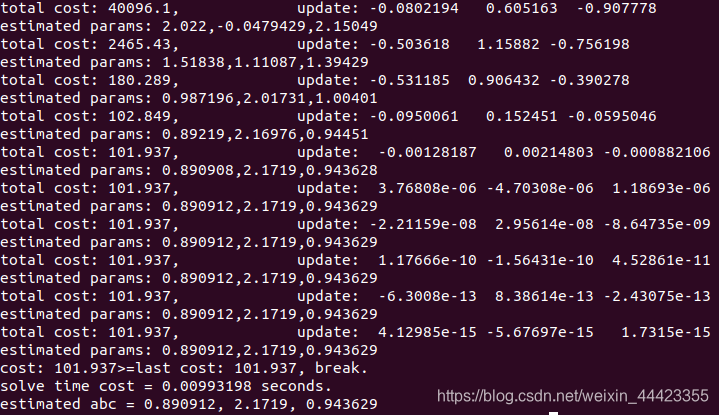

总结

非线性优化是一门经典课程，在slam中用于后端的优化。后端优化就是根据回环检测的信息和里程计推算的位姿，对地图和轨迹进行矫正。具体有待实践。

参考文献

[1]视觉slam十四讲-从理论到实践
[2]机械最优化设计