目录:
2.4.2 初步理解blob,layer,net以及solver
正文:
本章分为四个部分,整体秉承的是先讲理论再讲实践的原则。
首先,本章向大家展示一个曾经较为流行的问题:手写体数字的识别,这个问题在深度学习还没发展之前颇有难度。提出问题,肯定要解决,于是我们来到“神经网络”这个神秘事物的门口,这一节,我们初步认识神经网络,目的是要在脑中对它形成一个大体的概念。当然,仅仅知道大体的概念是不够的,我们还要更加深入,也就是这节要讲的经典网络模型:LeNet。讲完这个模型,是时候尝试实践了,我们将在最后一节中展示训练网络和测试数据的方法。
那么大体过程浏览了一遍,我们要开始进入正题。
2.1 问题定义
在人们开始学习编程时,大多数会选择从如何输出“HelloWorld”开始。同理,当我们作为新手面对深度学习这个陌生的领域时,第一个需要熟悉的就是手写体数字这个概念,以及它伴随的种种亟待解决的问题。
手写体数字识别一直是文字识别中的一个研究难题。为了便于研究,Mnist数据集被建立起来,它是由Yann LeCun主持创建的一个大型的数据库,保存着上万张的手写数字图片。这些数字图片已经进行了尺寸的标准化,并且图像均为黑底白字,其格式具有高度一致性。
如图2-1,我们可以看到Mnist数据集中的图片多种多样,这导致了对于机器来说较低的可识别性[1]。

图2-1 Mnist的部分数据
那么如此,我们便引入了一个难题——如何能够高效率、高准确率、低损耗地把这些龙飞凤舞的手写体识别出来呢?对于这个问题,人们已经发展出了很多种方法,比如基于笔划特征的算法、基于模板匹配的算法等。其中,基于笔划特征的算法是典型匹配算法的一种,包括笔迹分割和笔画匹配等步骤;基于模板匹配的算法要求于已存在的基础上建立起的标准的字符模板库,该算法将需要识别字符的特征表与已建立的模板库中的标准字符的特征表逐个比较。但这些早期的算法都需要人工设计特征提取器和分类器,也即匹配预测之前需要大量的人为设定,这导致泛化能力不够强,结果,对各类手写体的数字识别效果仍然不够理想。
在长期的进化过程中,深度学习的方法被提出,这给识别领域开辟了一个新的道路——利用神经网络原理达到目的。也就是说,在基于深度学习的概念上,我们把特征提取、预测判别这些步骤,更智能、更高度脱离人的提前设定,让机器自己琢磨出一套方法去识别图像。
那么,在以下的章节里,我们会详细介绍关于神经网络的基础知识,展现解决该问题的更高效方法。
【1】http://blog.csdn.net/simple_the_best/article/details/75267863
当人们在网上查询资料时会发现,利用深度学习知识,一张图片可以非常快速得到良好的预测效果,这个过程就像一个黑盒子,我们知道输入是图片、任务是分类、输出是预测结果,但是我们看不到里面发生了什么,也不知道那个黑盒子是什么,不要着急,后面会慢慢深入,我们先来一步步了解什么叫做神经网络。
人脑的神经细胞利用电化学过程交换信号。如图2-2所示,对于一个神经元,其它的一些神经细胞向这个神经元输入信号,当该神经元的兴奋状态基于某种规则被激发后,它会输出信号,发送到另一些神经细胞。这个过程,是信息传递里基本的单元,实际上人脑里的神经细胞的连接是复杂到不可想象的,是由高数量级的单元错综复杂地联结在一起的。
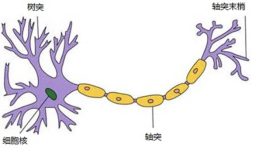
图2-2 人脑的神经系统
仿照神经元,我们直接提取出一个最简单的模型,如图2-3所示,输入信息经过神经元,被激活或者经过其它未知的处理后,输出新形式的信息。当然以下的模型肯定不能处理更加复杂的任务,所以我们要扩展模型的深度和宽度。

图2-3 提取简单的模型
理解前馈过程是理解神经网络体系的第一步。那么什么是前馈过程?把上节所说的基本处理单元“神经元”一层一层地连结在一起,形成层级结构,先理解成网络;网络的每一层神经细胞的输出都向前馈送到了它们的下一层,直到获得整个网络的输出为止,这一种类型的过程就叫前馈过程。其中,我们要着重理解到这些层级结构之间存在的联系,也即,每一层之间都有不同程度的连接,以便进行不同重要程度的信息交换。如下图2-4所示,图引自[1]
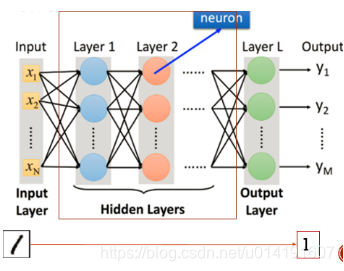
图2-4 前馈过程
一旦神经网络体系创建成功后,它必须接受训练来认出数字“1”,这个该怎么做呢?
很显然一开始这个黑盒子没有任何前期的经验积累,一次前馈过程后,预测结果会出错,说明这个模型不好,于是我们引出评估模型的说法,所使用的方法就是计算(真实值和预测值的)误差。
算得误差之后呢?别忘了我们的目标是——让网络正确的判断数字。
此时就要思考怎么让网络有更好的能力去识别图像,当然,我们有著名的反向传播来解决这点。通俗解释就是,把正确的画拿给最后一个人看(求取误差),然后最后一个人就会告诉前面的人下次描述时需要注意哪里(权值修正)。层层往回调整。当然,还是会有分类错误的情况,继续输入另一幅画,再来回一轮调整,直到最后网络输出满意为止。如下图2-5所示,引自[1]。
如此,我们就经历了一个最简单的网络形成过程,但是仅仅是知道大致概念还不行,下面我们将通过引入一个典型的深度卷积神经网络(Convolutional Nerual Network,也称CNN)模型来进行更细节的解剖。
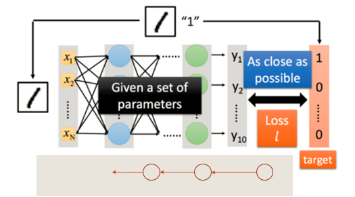
图2-5 反馈过程
[1] http://speech.ee.ntu.edu.tw/~tlkagk/courses_ML16.html
我们来到了CNN的结构剖析部分,在本节会全面介绍网络结构以及其中重点的知识解释,以便于以后更好的理解模型和使用模型解决问题。
如图2-6所示,这个网络结构是很早出现的,在神经认知机的概念提出后,LeNet横空出世,掀起一代深度学习浪潮。虽说网络结构的设计是很早之前,但其仍具有典型意义。图中我们可以看到这个网络中有两种层重复出现,一般形式为卷积层叠加下采样,这样的一套流程用于提取更高维特征。
经过两次卷积与下采样的处理后,输出的高维表达在两个全连接层里进行的整合,最后输出一个一维向量,表达预测结果。
图2-6是它的大概流程,下面来看每一层的具体情况,图引自[1]。
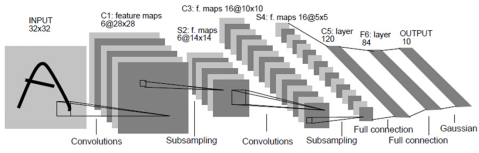
图2-6 卷积神经网络示例
首先,我们来看一下卷积网络中最重要的一种处理单元,卷积层。在理解卷积层之前,我们还需要知晓一些必要的基础知识。
如图2-7所示,对于数字图像中的像素表达,一般都以0到255之间的整数值作为像素值,在一张图像中,我们人眼看到的颜色对于计算机来说都是这些数值,整图对于机器来说就是一个矩阵,这是数字图像相关的基础知识,如果读者希望深入了解可以查阅冈萨雷斯所著的《数字图像处理》教材。


图2-7 数字图像的表达方式
在明确这个之后,再来学习卷积操作。卷积操作是对图像处理时,经常用到的一种操作,它具有增强原信号特征,并且能降低噪音的作用。
二维卷积操作公式:
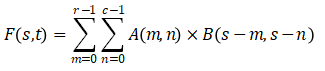
此公式是由一维的卷积公式扩展而来,对于图像而言,离散卷积的计算过程是模板翻转,然后在原图像上滑动模板,把对应位置上的元素经过处理,得到最终的结果[2]。我们来看一种更直观的对于卷积的理解方法——相乘相加,如下图2-8所示,图左表示一张原图像,也即上述公式的A矩阵,图右表示卷积核,也即公式里的值做了180°翻转的B矩阵。
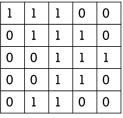
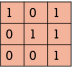
图2-8 卷积操作
每一个基础步骤,都要把卷积核与图像中对应范围的值一一对应相乘,如下图2-9左边所示,原图中的原值都与卷积核中对应位置的值进行数乘,最后将范围内的所有乘积值进行求和,这便是最一次单位操作,将最终值赋到图右的对应位置上。依此类推,卷积核像滑动窗口一样对所到范围进行不断地相乘相加,直至最后得到特征图。
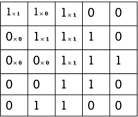
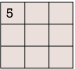
图2-9 卷积操作
解释完卷积的过程,我们不禁要想,这个卷积过程有什么意义?
根据公式可以看出,在进行卷积的过程中,实际上就是卷积核对图像信号筛选:
如图2-10所示,假设卷积核是的大小,卷积核的特点是在左上覆盖一些值。那么在原图像上卷积时,得到的特征图在左上部分会有更高的数值。也就是说,卷积核上的特点概念以某种方式映射到了原图像上,令原图像某个形状看起来很像核。
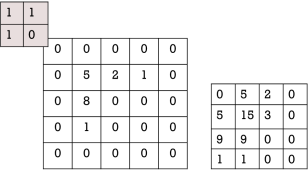
图2-10 卷积操作
原图像信号的筛选能力不仅仅可以针对左上的简单分布,多层的卷积核或者更复杂结构的卷积核都可以起到过滤高级特征的作用。卷积核设计越复杂,卷积层结构越复杂,输出将是表示了更高级的特征的激活映射。
当然这么一说还是比较抽象,我们使用一张普通图片,可以看到从卷积层出来后提取的特征图到底是什么样的。如图2-11所示,一些复杂的表征,比如方形、三角形、曲线的轮廓都被捕捉到了,卷积核的类似筛子的过滤作用尽显。
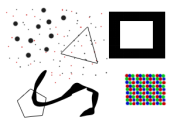
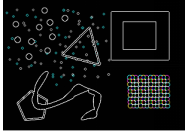
图2-11 卷积核提取特征
说到这我们要想起,神经网络中各个细胞单元都是层层连接,我们应怎么去看待这个连接的定义?
我们可以把层与层之间的连接理解为,在卷积层提取的特征图中,每一个像素值都是经过上一层原图中的一个感受野求解得到的,把这种求解关系看成一种连接。那么,这种连接,又是怎么影响下一层特征图的?卷积核,就是这个影响的主要贡献者。我们训练网络的时候要修改权值,这个权值指的就是卷积核里面的值。也就是说只有不断修改这个卷积核的值,才能改变卷积层的输出,以达到网络模型的修改的目的。
在此,我们引出了权值,也即参数的概念。如下图2-12所示,单次的卷积步骤中,存在着连接的概念,也即生成的结果与输入图中的感受野部分相连接。
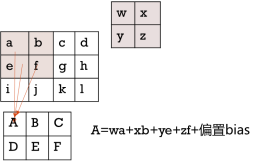
图2-12 卷积操作和连接的理解
同时,我们可以用下图2-13来理解前一个隐藏层和后一个隐藏层的图像元素之间是怎么连接的。如图2-13所示,左边方框内的字母代表原始图像中的二维矩阵元素展开成一维的数据,经过卷积操作后得到右边的圆形,这个操作所带有的卷积核值以某种方式将权重信息带到右边部分,也即输出的特征图。
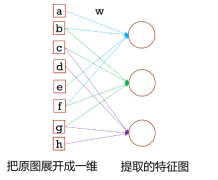
图2-13 层级之间的连接
如上图2-13,我们会发现,相比全连接的方法,卷积方法使得前层和后层的有效权重连接数量急剧减少,从这里我们先要有个概念,就是权值数量减少对于网络的计算和修改都是很有益处的。
本节对于二维的卷积理解暂时到这里,作为附加,我们可以先初步了解三维的卷积。如图2-14所示,三维卷积的输出依旧是一维的结果。
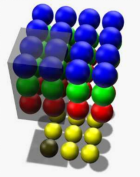
图2-14 三维卷积
讲完了以上的基础知识,我们来看实际的卷积层结构,如下图2-15所示。
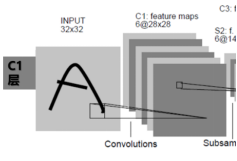
图2-15 C1卷积层
这一层名为C1层,它的一些必要信息如下:
输入:32x32 原图x
输出:28x28 特征图
卷积核:6个5x5——生成6个特征图
参数个数:6x(5x5+1)——156个可训练的参数
连接:在生成的特征图里,每个像素都与输入图像中的5x5个像素和1个偏置有连接,所以总共有15628x28=122304个连接。
权值共享:特征图上每个像素对应的参数是共享的,因为卷积核作为权值在连接下一层的时候不存在有多少连接就有多少权值的情况,他只有一个情况,就是卷积核本身,对于输出图来说,每一次做卷积,只有一个核在对整个图的各个部分滑动,连接数量远大于要修改的权值数量。
除了C1层,还有一层相似的卷积层C3,C1和C3之间还有一层下采样层,如下图2-16所示[1]。
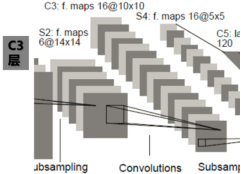
图2-16 C3卷积层
这一层的必要信息如下:
输入:6个14x14 特征图
输出:16个10x10 特征图
卷积核:6个5x5
参数个数:如下图2-17左所示,行代表最后生成的特征图,列代表输入的6张图,X表示对于第n张输入图使用卷积核,得到第n生成图,计算方式如下[1]。
6<张生成图x(3<个卷积核>x5x5<卷积核大小>+1<偏置>)
+6x(4x5x5+1)
+3x(4x5x5+1)
+1x(6x5x5+1)=1516个参数
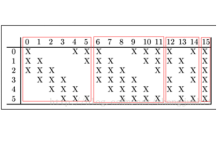
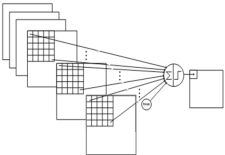
图2-17 卷积层连接方式
池化层在这个网络结构中于卷积层连接,它主要做的工作就是把图像的内容进行一定程度的降维,提取主要特征,剔除冗余信息。如下图2-18所示,池化较常用两种方法,其中的Max Pooling操作将挑选固定窗口范围里的最大值,作为输出图的对应值;Average Pooling操作将窗口中的值求平均,以其作为输出图的对应值。
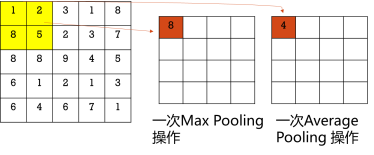
图2-18 池化操作
在LeNet中,这样的池化层有两个,分别是S2和S4,穿插在卷积层之间,他们的都是利用一样的Max Pooling池化方法进行下采样的。
图2-19 汽车超车
池化层S2信息如下:
输入:6个28x28 特征图
输出:6个14x14 下采样图
池化所用的窗口:2x2 在这个范围内求值
参数个数:2x6=12 当S2层对窗口内的像素求最大值后,再给最大值乘以权值、加上偏置,作为该层输出
池化层S4信息如下:
输入:16个10x10
输出:16个5x5
池化所用的窗口:2x2
参数个数:2x16=32 理解方式与S2层相同
LeNet加入池化层有一些重要意义。对于计算机视觉的处理图像过程来说,如果一开始就是把细节信息纳入考虑,那么视觉系统对于全局的图像概念就会削弱,这会把神经活动更加复杂化。那么,引入池化便是为了仿照了人类的降维方式,将图像先进行抽象。池化操作中,区域的汇合和抽象使得模型更加注重与某种特征的形态,比如线、圆等,而不是这个特征的具体方位,因为在模型中,识别过程对于位置精细度的要求不高;不仅如此,区域抽象还使得计算量减少,这对于模型的性能是一种提升[1]。
举个例子,如下图2-20所示,无论左边的两张图中窗口里最大值位置怎么变化,到最后进行池化的时候,最大值被抽取出来,细节的位置信息被忽略,但特征被强调了,输出的图都是相同的。
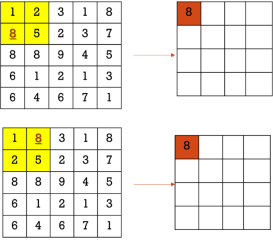
图2-20 池化操作的意义
在CNN中的全连接层一般都用于对前层的所有特征图做加权和,它的输出与输入都有关联,相当于一个卷积核大小为11的卷积层,输入图内的所有像素输出图的所有像素都有权重连接。全连接层里巨大的参数量以及难以保存空间结构的缺点,使得它在现今的深度学习研究中越来越不被看好。
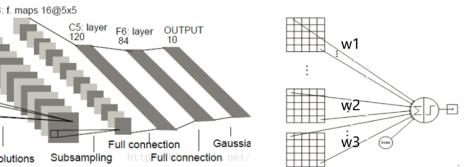
图2-21 C5全连接/卷积层
如上图2-21所示,全连接/卷积层C5信息如下:
输入:16个5x5 特征图
输出:120个一维卷积结果,成列
卷积核:5x5 120个
参数:(5x5x16<个卷积核>+1)x120<个卷积结果>
每个卷积结果都是与上一层的16个图卷积后合成得到的
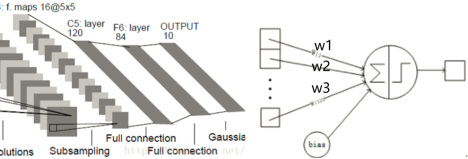
图2-22 F6全连接层
如上图2-22所示,全连接层F6信息如下:
输入:120个卷积结果
输出:84个节点
参数:(120+1)x84 每个节点与上一层的120个节点连接
F6层的下一层是OUTPUT层,信息如下:
输入:84个节点,与一种7x12的bit标准图比对
输出:预测值(0~9)
OUTPUT层预测方法有多种,其中可以使用欧式径向基函数,输出层由欧式径向基函数单元组成每类一个RBF单元,每个RBF单元有84个输入节点。每个RBF单元计算输入和基准(也就是7x12的bit标准图,各自对应数字0到9)之间的欧式距离。输入离基准越近,RBF输出的越小,越接近某预测值。这些单元的基准是人工选取并保持固定的[1]。
另外,更常用的分类预测方法是利用softmax函数得到一个概率取值,它的输出对于每个数字都有概率表达,选取概率最大的对应数字,即为最终的预测结果。
主要的处理层都在上面提到了,但对于LeNet,还存在一个不可或缺的非线性化处理单元,也即激活层。
激活层就是一个激活函数。对于普遍的神经网络模型,激活函数在每层的处理中都是必要的,它将每层的输出都加入了非线性因素,使得线性模型的表达能力增强。为什么单纯的线性模型表达能力弱?设想神经网络函数是线性的,那么反馈求导过程中,不论是哪一层的导数都是常数,这意味着梯度和输入无关了,输入的变化不会影响模型的反向传播修改权重的过程。
有几种典型的激活函数一直在神经网络研究中活跃,其中着重介绍两种激活函数,Sigmoid和Relu。
Sigmoid函数如下公式所示:
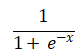
Sigmoid函数的图像以及其导数的图像如下图2-23所示:
我们可以发现,该函数两侧平坦,导数两侧的值接近于0,当输入接近两侧时会造成信息丢失,从而无法完成深层网络的训练。
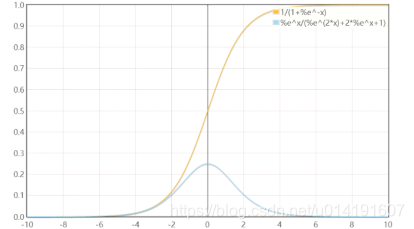
图2-23 Sigmoid函数
激活函数ReLU函数如下公式所示:
![]()
ReLU的导数图像不存在向某侧趋于0的现象,故减小的梯度消失(下节会详细解释对于梯度消失的理解)的风险。其次,ReLU会使一部分神经元的输出为0,增大了网络的稀疏性。当输入小于0,该层的输出为0,训练完成后为0的神经元越多,稀疏性越大,提取出来的特征就约具有代表性,泛化能力越强。
通常,一个好的激活函数应该具有以下性质[3]:
(1)非线性。线性激活层对于深层神经网络没有作用,因为其作用以后仍然是输入的各种线性变换。
(2)连续可微。神经网络的数学基础是处处可微的,选取的激活函数要能保证数据输入与输出也是可微的。
(3)范围最好不饱和。如sigmoid函数,反向传播时容易出现梯度消失的情况。
到这里我们来梳理一下,如下图2-24所示,这个网络从图像输入到输出经历了若干个复杂的层处理过程,要注意在这个过程中它一直是向前运行的,而且每一层的输入都是上一层的输出。
在这个过程中,图像经过网络模型的解读,得到了一个可能带有误差的结果,这个结果很可能不令人满意,那么,就需要更改模型参数。
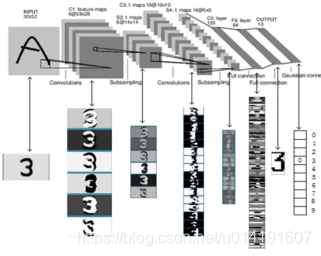
图2-24 网络模型
为了便于理解,假设一个单参数单神经元模型,表达如下:
![]()
其中,w代表权重,xi代表输入的第i个样本。
对于前向计算阶段,在经过前向过程到达最后的OUTPUT层时,损失函数(误差函数、目标函数)为
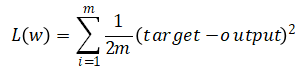
其中,m为样本个数。表达出误差计算方法后,我们来看如何进行对于模型的反馈。
我们要明确目标:反向传播的训练过程是用于调整权重的。对于单层网络来说,就是网络输出对输入的连接权值求导的过程。
为何要选择求导?其实这就是让目标函数能够以最快的方向的下降直到极小值,也即最优值。但是一次的训练是不能使模型达到的最优值的,于是,我们为了让权值不断更新,采取不断把数据分批次喂给模型进行训练,一步一步地使得目标函数值下降,通过这样的不断更新权值去逼近目标函数的最小值。这个过程被称之为梯度下降,如下图2-25所示。
基于图中所示的模型,整个过程也就是一套三部曲:
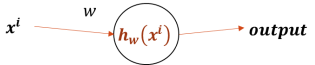
图2-25 单神经元的模型
1) 前向计算误差函数
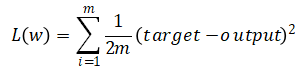
2 ) 反向传播
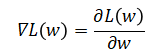
3) 权值更新,为了使L(w)不断减少,计算(即![]() ,权值的更新值)从而更新w
,权值的更新值)从而更新w
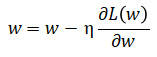
以上公式中有一个学习率的概念,这是在实际训练的时候很值得斟酌的一个值。我们可以把学习率理解为我们平常所说的“度”,在训练过程中不仅要控制学习的速率,也要考虑上一次更新的速率对这一次的更新值的影响,把握模型更新的速度和走向,避免出现跳跃性的更新,永远无法到达最优值。
三部曲的最终目标是为了使得损失函数能够达到极小值,为了方便理解,如下图2-26所示,顺着黑色箭头我们可以看到,为了达到函数的底端,这个更新过程的轨迹逐渐向下逼近函数的底端
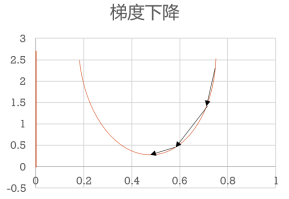
图2-26 梯度下降示例
单层的网络预测能力是远远不够的,我们需要建立更深层次的网络。但此时,网络模型的反向传播过程会出现一些问题,其中一个比较典型的,就是梯度消失。
要说到梯度消失问题,就不得不说到如何理解梯度下降的数学过程。
在多层的网络中,梯度求解过程是什么?说白了就是求导过程的链式法则,一层网络的求导只是单次的输出对输入求导,多层的求导就是每一层展开连续求导。
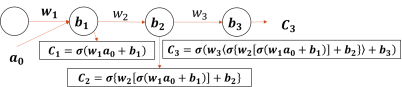
如图2-27所示,每一层的输入输出都展开为表达式,并且进行了反向逐层求导。在使用链式法则后,展开得到表达式![]() ,如果使激活函数为Sigmoid函数,显然
,如果使激活函数为Sigmoid函数,显然![]() ,此时随着网络层数加深,分数的连续乘积会导致最终的求导公式趋于0,如此一来更新权值就没有意义了.
,此时随着网络层数加深,分数的连续乘积会导致最终的求导公式趋于0,如此一来更新权值就没有意义了.
![]()
图2-27 梯度消失示例
那么至此回顾一下,在这一节中,我们了解到,反向传播过程在数学上可以被理解成求导的链式法则,形象地可以理解为将每一层的输出与该层输入求导,并更新该层权值的过程。其中我们又提到,激活函数的选取对于反向过程和模型表达能力都很重要,但具体怎么选取,我们会在将来的课程中逐渐引出。
到这里我们就讲完了关于CNN的较为基础的理论,在对这个网络结构有了初步认知之后,我们开始进入实操。
[1] Yann LeCun.Gradient-Based Learning Applied to Document Recognition[J].Proceedings of IEEE 1998: 7-1
[2] https://www.zhihu.com/question/27251882
[3] https://en.wikipedia.org/wiki/Activation_function
2.4 深度学习工具——Caffe
实操需要有一个平台,我们在这里介绍一种能够帮助我们去理解CNN模型的平台——Caffe。
这个平台也可以称作工具,本书会在这个部分展开,从预览到实践,一步步去体现这个网络和Caffe工具是怎么对应的,也希望在这一节教会大家简单明了地使用caffe训练模型,以及用其测试Mnist手写数据集的全过程。
我们首先来预览Caffe目录的内部文件组成。如下图2-28所示,这个目录已经完整地将Caffe里面的所有文件都展示了出来,但是由于乍一看下东西实在略多,所以我们先来看看这一节中我们可能会用到的一些重点的部分。
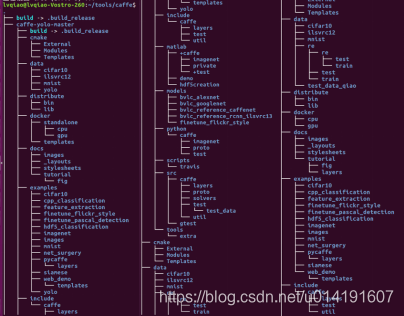
图2-28 Caffe目录
上图展示的是include和src两个目录,Caffe的实现主要围绕这两个文件目录下的代码展开,这两个目录在层次上是基本一一对应的。
如下图2-29所示,include目录内主要包含了实现Caffe底层基础功能的代码头文件,src包含的是底层源码。
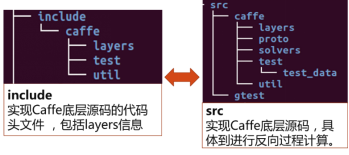
图2-29 include文件和src文件
下图2-30展示的是data和examples两个目录,data目录包含原始数据和与数据处理相关的源码,examples目录主要包含典型的、简单的深度学习项目源码。在使用Caffe进行实验的时候,我们可以从项目实例中获取一些源码的内容并模仿使用。

图2-30 data和examples文件
2.4.2 初步理解blob,layer,net以及solver
在介绍完以上几个重要的目录部分之后,本书再来带大家了解使用Caffe之前必须要知道的一部分概念
Caffe 说白了,是由Blob,Layer,Net,Solver这四个部分串起来的。我们在理解的Caffe代码的顺序是:
Blobs ——存储、交换网络中正向和反向传播时的数据和导数信息。
Layer ——模型中的层结构。
Net ——一系列层和其连接数据的集合。
Solver——优化器功能的设定和超参数设置,用于网络里的误差以及梯度计算。
在这四个概念的贯彻下,我们的模型得以正常进行训练[1]。
关于Blob我们首先要知道的是,从数学意义上说,Blob是连续存储的数组结构;它常规的维数是图像数量(N)×通道数(C)×图像高度(H)×图像宽度(W);它的各类定义位于底层函数blob.cpp,头文件位置是 ./include/caffe/blob.hpp,源文件位置是 ./src/caffe/blob.cpp。
Blob是处理和传递数据的封装包。它的头文件以及源代码就存放在Caffe根目录的include文件夹和src文件夹里。之所以要提到这个,是因为这些底层文件对于我们平时更深层次去理解Caffe框架很有用,在使用Caffe时对于底层文件的理解有时能够帮助我们设计整体的项目。如下图2-31所示,Blob在网络中相当于在层与层之间传递数据的容器。
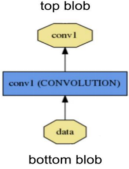
图2-31 Blob与Layer
Caffe十分强调网络的层次性,也就是说如卷积操作,非线性变换(ReLU等),Pooling,全连接层等全部都由某一种Layer来表示。对于一个Layer来说,它的bottom(底部数据端)是接收数据的,top(顶部数据端)是输出数据的。其次,一个Layer可以处理两种方向的运算——Forward(前向)和Backward(反向),前向是从bottom到top的方向,对输入的blob进行计算处理;反向是从top到bottom,计算其相对于输入的梯度[2]。
Layer相关的基础操作都保存在Caffe的底层文件里,它的头文件位于./include/c-
affe/layer.hpp,源文件位置是 ./src/caffe/layer.cpp。
Layer和blob,这两个元素共同构成了Net。通过下图2-32我们可以看到,Net中的Blob对象是用于存放Layer输入或输出的中间结果,Layer则根据Net的描述(也就是prototxt文本文件),对指定的blob做某些计算处理(如卷积)。
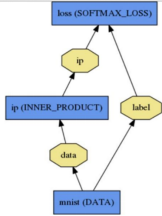
图2-32 Layer与Net
那么到最后Solver这一个部分了,首先观察每一次迭代过程solver做了什么:
1. 调用前向过程计算出输出和误差;
2. 调用后向过程计算出梯度(误差函数对每层的权重w求导);
3. 更新权值,反复迭代优化模型;
4. 调整自己作为求解器的状态,如降低学习速率。
它的头文件位置是./include/caffe/solver.hpp,源文件位置是 ./src/caffe/solver.cpp。
总的来说,Solver通过协调Net的前向推断计算和反向梯度计算,来对参数进行不同方法的优化更新,同时调整自己的状态,从而达到减小目标函数的目的。
以上所讲,还只是架构基础,可能读者仍对于实际的过程比较茫然。那么接下来本书呈现一遍这个过程,也就是运行Caffe自带的这个手写体数字识别的例程,让大家先来感受一下,一个经典的CNN模型在Caffe的框架上是怎么实现的。
在实操之前,本书会先展示一个大体的流程,在测试模型、训练模型完成之后,再来讲解过程中重要的步骤,也就是决定这个LeNet网络的蓝图——模型描述文件。最后,本书会将网络训练过程中数据流动的可视化,以便于大家更加深入体会和理解网络模型。
第一步是用一张自己的图片测试已经训练好的模型。Caffe工具里有一个示例代码,它调用训练好的模型预测结果值,代码名为classification.cpp,源码中的main()中申明了他的用法——输入是deploy.prototxt(测试网络的模型描述文件),network.caffemodel(调用的已训练好的模型权值文件),mean.binaryproto(训练图像的均值文件),labels.txt(标签种类文件,比如0-9,按行编写),img.jpg(输入的图像)。
在源码中,它实际调用的是Caffe底层的前馈过程的计算函数,net_->Forward(),也就是说,这个模型在测试的时候,走了一遍这个已经训练好的网络的前向过程,直到最后预测层输出结果。
以下为classification.cpp代码中的一部分:
int main(int argc, char** argv) {
if (argc != 6) {
std::cerr << "Usage: " << argv[0]
<< " deploy.prototxt network.caffemodel"
<< " mean.binaryproto labels.txt img.jpg" << std::endl;
return 1;
}
可以看出,源码所需要的输入参数部分包含了网络结构文件、已训练好的模型、均值文件、标签和图片。运行脚本,输入代码中要求的文件,即可进行测试。然后,我们开始看看这个训练好的模型是如何得到的,也就是说——如何训练模型。
模型的训练步骤如下:
1) 数据准备
下载数据集并解压,Caffe自带源码
./caffe/data/mnist/get_mnist.sh
二进制文件转成levelDB或LMDB数据库的格式
./caffe/examples/mnist/create_mnist.sh
计算 mnist_train_lmdb 的均值文件
./caffe/examples/mnist/compute_mean.sh
2) 训练模型,运行模型描述文件蓝图
./caffe/examples/mnist/train_lenet.sh
3) 利用训练好的模型权值文件进行预测
./caffe/examples/mnist/test_caffenet.sh
以上脚本代码都存在于caffe自带的框架中。
我们来一一讲解对于每个步骤的理解。
1) 数据准备
数据下载完成后,我们会在指定的文件里发现四个如下名称的二进制文件,这便是最原始的二进制数据了。
train-images-idx3-ubyte —— 训练图像
train-labels-idx1-ubyte —— 训练标签
t10k-images-idx3-ubyte —— 测试图像
t10k-labels-idx1-ubyte—— 测试标签
转换为LMDB数据库后,我们会在指定文件夹里看到如下图2-33所示的两个文件,这说明生成成功。
图2-33 lmdb格式的文件
图片减去均值后,再进行训练和测试,会提高速度和精度。因此,一般在各种模型中都会有这个操作。那么这个均值怎么来的呢,实际上就是计算所有训练样本的平均值,计算出来后,保存为一个均值文件,在以后的测试中,就可以直接使用这个均值来相减,而不需要对测试图片重新计算。
2) 训练模型,运行模型描述文件蓝图
先不急着训练,我们先来看一下模型训练的依据是什么。打开训练的脚本观察他的调用路线——训练模型的脚本内容如下:
./build/tools/caffe train --solver=examples/mnist/lenet_solver.prototxt $@
其中,caffe.bin是执行者,调用编译好的build/tools/caffe.bin 文件,全过程都由它来操纵,它所依据的盖房子的蓝图是.prototxt文件,指定了求解器(包含模型文件和训练超参数)——lenet_solver.prototxt,这个文件内对于超参数各项解释均有注释。实际网络构成中,一些初始化的超参数是可以人为设定的。
求解器指定的网络模型描述文件——lenet_train_test.prototxt,求解器内的相关代码如下。
# The train/test net protocol buffer definition
net: "examples/mnist/lenet_train_test.prototxt"
此时我们追踪到他的蓝图文件是lenet_train_test.prototxt,也即网络模型描述文件.prototxt——这就是我们平常会加工的地方,对于网络结构的设计就在于这里。
本文在.prototxt上选取了几个部分,显示的是LeNet里面的几个典型的层,比如池化层,激活层,最后计算误差的层。
其实做到这里,我们发现模型的训练一个脚本就可以解决,但是实际上运行这个工程的是已经编译好的caffe.bin来做的,在训练过程中,我们会看到命令行中飞过很多信息,这些信息就是告诉你运行的细节,具体的过程如下:
1.确定装修方案——
创建训练网络
盖楼:phase :train 各层layer(输入输出)
统计哪些层需要反传
创建测试网络
盖楼:phase :test
2.测试、训练…测试、训练…快照…
3.最终准确率和loss较好,训练完成
4.模型权值保存到caffe/examples/mnist/lenet_iter_10000.caffemodel
到目前为止,我们的mnist例程已经运行完成了,我们现在初步了解到一个完整的深度学习系统较为核心的操作步骤了。
在训练网络的时候,本文提到过核心的网络模型描述文件,现在我们来一层层搭建这座阁楼。要首先记得,这个网络模型描述文件就代表了网络结构是如何的,所以一般对于结构和一些初始参数的创建都在这个.prototxt文件里。
如图2-34所示,这是流程图化的模型架构。左边是架构中每一层的名称以及卷积核大小,右边是输出图像的数据维度
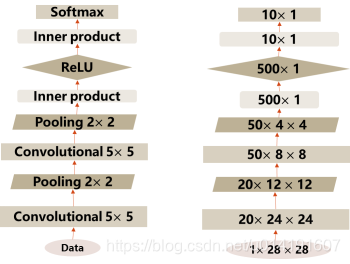
图2-34 模型架构的流程图
蓝图文件把输入图像大小、输出大小、卷积核大小等等硬性要求列了出来,根据这个模型的架构,我们开始学着层次化地定义网络结构:
1)数据层
layer {
name: "mnist"//名称mnist
type: "Data"//类型data
top: "data"
top: "label"
include {
phase: TRAIN
}
transform_param {
scale: 0.00390625//缩放传入的像素
}
data_param {
source: "examples/mnist/mnist_train_lmdb"//从给定的lmdb源读取数据
batch_size: 64//批处理大小64
backend: LMDB
}
}
具体来说,这个层有名称mnist,类型data,并从给定的lmdb源读取数据。我们将使用64的批处理大小,并缩放传入的像素,为什么0.00390625?它是1除以256。最后,这一层产生两个输出,一个是data,一个是label。
2)卷积层
layer {
name: "conv1"
type: "Convolution"
bottom: "data"
top: "conv1"
param {
lr_mult: 1//权重学习率
}
param {
lr_mult: 2//偏置的学习率
}
convolution_param {
num_output: 20//输出20张特征图
kernel_size: 5//卷积核大小
stride: 1//步长1
weight_filler {
type: "xavier"//初始化权重的方法
}
bias_filler {
type: "constant"
}
}
}
这个层有名称conv1,类型Convolution,设置了权重的学习率和偏置的学习率,以及初始化权重的方法。该层会输出20张特征图,并且定义了55的卷积核。最后,这一层产生一个输出,conv1。
3)池化层
layer {
name: "pool1"
type: "Pooling"
bottom: "conv1"
top: "pool1"
pooling_param {
pool: MAX//池化方式
kernel_size: 2//窗口大小
stride: 2
}
}
具体来说,这个层有名称pool1,类型Pooling,设置了池化方式Max Pooling,窗口大小为22,步长为2,意味着每次移动窗口的距离为2。最后,这一层产生的输出是pool1。
4)全连接层
layer {
name: "ip1"
type: "InnerProduct"
bottom: "pool2"
top: "ip1"
param {
lr_mult: 1
}
param {
lr_mult: 2
}
inner_product_param {
num_output: 500
weight_filler {
type: "xavier"
}
bias_filler {
type: "constant"
}
}
}
具体来说,这个层有名称ip1,类型InnerProduct,这一层产生输出ip1。
5)激活层
layer {
name: "relu1"
type: "ReLU"//激活函数选用ReLU
bottom: "ip1"
top: "ip1"
}
激活层选用的函数是ReLU,输入和输出都是ip1。
6)计算准确率
layer {
name: "accuracy"
type: "Accuracy"
bottom: "ip2"
bottom: "label"
top: "accuracy"
include {
phase: TEST//在测试阶段才使用
}
}
这一层往往在测试的时候使用,只计算预测结果与真实值的是否对应,以计算准确率。
7)损失函数层
layer {
name: "loss"
type: "SoftmaxWithLoss"//计算方法是softmax函数
bottom: "ip2"
bottom: "label"
top: "loss"
}
该层有两个输入,接收预测结果和真实值,然而不会产生任何输出,只是计算这一层基于输入ip2(预测结果)的损失函数。此时,反向传播开始,整个模型的权重的逐渐进行优化,一切魔法自此开始。
在上一小节里,我们知道了网络描述文件里对应的LeNet是怎么样部署的,但仅此还不够,对于整个网络的图像数据流动,我们尚不清楚。因此,本节尝试运行一个提前编写好的可视化程序,对应着这个模型,使用ipython notebook把每一层的输出的特征图、池化图,都显示出来。如图2-35所示。

图2-35 每一层特征图可视化
上图2-35展示了每一层的输出,对于图像的特征一层一层被提取的概念将有更形象的理解,到最后我们会发现原图像被这个模型理解成了一个很抽象的概念,人眼已经难以辨别了。然而,这些抽象化对于机器的计算过程来说更具有操作性,也就是说更底层,可执行度更高。
输出的预测结果如下图2-36所示:
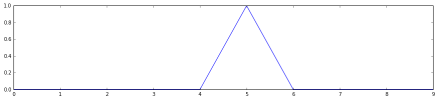
图2-36 输出的预测结果
可以看到,最终判断原图文字为5,这是正确的。
那么到现在,本节进行了一遍完整的训练LeNet的流程,也对训练过程中最重要的网络结构描述文件进行了详解。
至此本章展示的是一个比较易于新手理解的内容,对于图像分类这个老问题,读者不仅可以实践,还能够认识到经典的神经网络模型的建立和推导。当然,熟悉caffe不是一两个小时就能够轻易达到的.
[1] https://www.zhihu.com/question/27982282
[2] http://blog.csdn.net/myarrow/article/details/52227548