A NEW COEFFICIENT OF CORRELATION文献阅读

知乎上有一篇文章有简要介绍该文献中的主要成果。这篇博文对该文章的每一部分进行简介。

摘要中明确说了在此之前还没有任何一个相关系数满足以下三个条件中的任意一点，而该文章中提出的相关系数同时满足下列三个条件：

• 形式简单容易计算；
• 取值为0当且仅当变量之间独立；取值为1当且仅当其中一个变量是另一个的可测函数；
• 在独立性假设下有简单的渐进理论性质。

引言首先介绍了3个经典的相关系数的各自的局限性以及共同的缺陷，那就是即使在完全没有噪声的情况下，它们也不能有效地检测非单调的关联。然后回顾了现有研究中对经典系数这一重大缺陷的改进后的度量系数，紧接着又指出了这些改进方法的所存在的共同局限性：

• 这些系数大多是为了测试独立性而设计的，而不是为了测量变量之间关系的强度。 理想情况下，当且仅当一个变量看起来越来越像另一个变量的无噪声函数时，人们希望系数接近其最大值，就像皮尔逊相关性接近其最大值时，当且仅当一个变量接近另一个变量的线性函数（无噪声情况下）；
• 在独立性假设下，这些系数没有简单的渐近理论性质，这不利于快速计算P值以检验独立性。

文章提出的度量系数的简单形式如下：

此时没有完全重合的数据对$(X_i,Y_i)$。其中$r_i$表示将数据对按照$X_i$进行顺序排列后$Y_i$的秩。

定理1表明 ${\xi }_n$ 是随机变量$X$和$Y$之间依赖性度量的一致估计量。即${\xi }_n\to \xi ,a.e.$。

定理1
如果Y几乎处处不等于常数，则当$n\to +\infty$时，${\xi }_n$几乎处处收敛到确定性极限：

其中$\mu$是Y的密度（我猜的，原文是law）。这个极限的取值范围为[0,1]，取值为0当且仅当X和Y独立，取值为1当且仅当存在实数域上的可测函数使得$Y=f(X),a.e.$

注：

1. 该度量系数不是对称的，其目标是探究Y是否是X的某一函数。若想要获得对称性的系数可以通过取$\mathrm{m}\mathrm{a}\mathrm{x}\{{\xi }_n(X,Y),{\xi }_n(Y,X)\}$来实现；
2. 从$\xi$的形式上看，显然$\xi$满足以下性质。但是第二个性质的逆命题的证明会比较复杂，以及${\xi }_n\to \xi ,a.e.$这个结论不是那么明显。
   • 取值范围为[0,1];
   • 当X和Y独立时，$\xi =0$；当Y是X的可测函数时，$\xi =1$.
3. 定理1仅仅对Y有要求且仅要求Y不是常数。即X和Y可以是连续的、离散的厚尾分布的等等。
4. ${\xi }_n$对严格单增的函数变换具有不变性。即${\xi }_n(X,Y)={\xi }_n(g_1(X),g_2(Y))$，其中$g_1,g_2$是严格单增函数。这是因为${\xi }_n$的计算是基于秩的，正因如此，其计算速度也很快，用时$\mathcal{O}(n\log n)$.
5. 可以拓展到多元变量的相关性度量系数。
6. 若$X_i$有重复观测，${\xi }_n$带有随机性，这个随机性是由排序时为打破重复性带来的，n很大时可以忽略。另一种方法是取所有可能的排序下的${\xi }_n$的平均。
7. 若$Y_i$无重复观测，，，
8. ！！！有现成的R包XICOR可以计算${\xi }_n$，这个包还可以用上述统计量进行独立性检验。

第二章——理论研究
在第二章中，作者指出${\xi }_n$的主要用处是提供一个X和Y之间关系强度的度量，而不是作为检验独立性的检验统计量。然而，如果需要也可以使用它来测试独立性。因为它有简单的独立渐近理论性质。定理2给出了在独立假设和Y连续假设下$\sqrt{n}{\xi }_n$的渐进分布。然后给出了在无连续性情况下更一般的渐近理论性质。

定理2.1
假设X和Y是独立的且Y是连续的，则$\sqrt{n}{\xi }_n\to N(0,2/5)$
注：

1. 上述分布的收敛速度很快，即使n小到了20仍然如此。
2. 上述Y是连续的，对于Y不连续的情况，方差会发生相应变化，并且此时方差可能依赖于Y的真实分布。这就引出了定理3.

定理2.2
假设X和Y是独立的且Y是连续的，则$\sqrt{n}{\xi }_n\to N(0,{\tau }^2),n\to +\infty$，其中，

其中$Y_1,Y_2,Y_3$与$Y$独立同分布，$\varphi (y,y^{\prime })=\mathrm{m}\mathrm{i}\mathrm{n}\{F(y),F(y^{\prime })\},F(t)=\mathbb{P}(Y\le t),G(t)=\mathbb{P}(Y\ge t)$。当Y不是常数时${\tau }^2>0$恒成立，且若Y连续则${\tau }^2=2/5$.

当Y连续时显然$F(Y),G(G)\sim U(0,1)$，则$\tau$的值不依赖于Y的具体分布。若Y离散，$\tau$的值可能会依赖于Y的具体分布。例如，若$Y\sim Bernoulli(1/2)$，则${\tau }^2=1$。
当Y离散时，有下列方法可以从数据中估计${\tau }^2$：

其中，


$u_1\le u_2\cdots \le u_n$为$R(1),...,R(n)$的递增重排序列，$v_i={\sum }_{j=1}^i{u}_j,i=1,...,n.$
由此引出以下定理。

定理2.3
估计量${\hat{\tau }}_n^2$计算的时间成本为$\mathcal{O}(n\log n)$，且${\hat{\tau }}_n^2\to {\tau }^2,a.e.$

在第二章结尾的部分，文章指出，当X和Y相关时，$\sqrt{n}({\xi }_n-\xi )$依然是渐进正态的。对称化统计量$\mathrm{m}\mathrm{a}\mathrm{x}\{{\xi }_n(X,Y),{\xi }_n(Y,X)\}$在独立性假设下，很可能表现为一对相关正态随机变量的最大值。当然，使用对称化统计量很容易进行独立性的置换检验。

第三章——案例1：高尔顿的豌豆

作者首先说明了数据的来源以及获取的途径：弗朗西斯·高尔顿爵士1875年收集的peas数据是统计史上最早、最著名的数据集之一。这些数据包括700次对母株和子株中甜豌豆平均直径的观察。未正确记录数据收集的确切过程；我们所知道的是，高尔顿向朋友们发送了一包包种子，朋友们播下了种子，种植了植物，并将新植物的种子送回了高尔顿（更多细节见[43，p.296]）。该数据集在R中的psych包中作为“peas”数据框免费提供。

设X是母植物中豌豆的平均直径，Y是子植物中豌豆的平均直径。正如皮尔逊很久以前所观察到的那样，X和Y之间的相关性约为0.35。由于$X_i$在该数据中有许多重复值，这意味着${\xi }_n(X,Y)$是随机的。对一万次模拟进行平均后，${\xi }_n(X,Y)$的值接近0.11。独立性测试的P值小于$10^{-4}$。因此在本数据中${\xi }_n(X,Y)$成功检验出了X和Y之间不独立。

第5章
案例2：酵母基因表达数据
在《基因表达研究》（gene expression studies）中的一篇里程碑式的论文中，作者研究了6223个酵母基因的表达，目的是确定其转录水平在细胞周期中振荡的基因。从外行的角度来看，这意味着对表达进行了多个连续时间点的研究（准确地说是23个），目的是识别转录水平遵循振荡模式的基因。此示例说明了相关系数在模式检测中的用处。因为基因的数量如此之多，通过视觉检查来识别模式是不可能的。

该数据集被用于论文《Detecting novel associations in large datasets》中，以证明MIC在散点图中识别模式的有效性。该文作者使用了数据集的一个精心策划的版本，他们排除了所有缺少观察的基因，并进行了其他一些修改。修改后的数据集有4381个基因。我使用这个精心策划的数据集（可通过R软件包minerva获得）研究${\xi }_n$在发现具有振荡转录水平的基因方面的能力，并将其性能与模拟中的竞争方法进行比较。

对于每项测试，均获得P值，并使用Benjamini–Hochberg FDR程序选择一组重要基因，错误发现的预期比例设定为0.05。

结果表明，在4381个基因中，有215个基因是通过${\xi }_n$选择的，而不是通过其他测试选择的。这本身令人惊讶，但更令人惊讶的是这些基因的性质。图6显示了前6个基因的转录水平（即P值最小的基因）。毫无疑问，这些基因表现出近乎完美的振荡行为，但它们并没有被任何其他测试选中。

人们可能想知道，这是否只适用于前6个基因，或者是所有215个基因中的典型基因。为了调查这一点，我从215个基因中随机抽取了6个基因，并观察了它们的转录水平。结果如图7所示。

即使是随机样本，我们也看到了强烈的振荡行为。这种行为在其他随机样本中得到了一致的观察。

第四章——数据模拟
目的是通过数值模拟研究${\xi }_n(X,Y)$的性能，并将其与其他方法进行比较。我们比较了一般性能、运行时间和测试独立性的能力。

4.1. 一般性能、公平性和通用性。

上图给出了${\xi }_n(X,Y)$作为关联度量的一般性能。该图有三行。每一行从散点图开始，其中Y是X的无噪函数，X由上的均匀分布生成[−1, 1]. 当我们向右移动时，会添加越来越多的噪声。在每种情况下，样本量n取100，以表明${\xi }_n(X,Y)$在相对较小的样本中表现良好。在每一行中，我们看到对于最左边的图，${\xi }_n(X,Y)$非常接近1，并且随着我们添加更多的噪声而逐渐恶化。

根据定理2.1，在独立假设下，当n=100时，${\xi }_n(X,Y)$的0.95分位数为0.066。图2中的值都比这高得多。

上图中一个有趣的观察结果是${\xi }_n(X,Y)$似乎是一个公平系数。公平性的定义在数学上并不精确，但在直觉上很清楚。粗略地说，一个公平的相关性度量“对不同类型的同等噪音的关系给出了相似的分数”。上图表明，只要关系是“函数式的”，${\xi }_n(X,Y)$就具有此特性。对于非功能性的关系来说，这是不公平的，尽管这是预期的，因为${\xi }_n(X,Y)$衡量X可以预测Y的程度。

衡量相关性的另一个标准是，系数应该是“一般的”，因为它应该能够检测散点图中的任何类型的模式。在统计方面，这意味着基于系数的独立性测试应与所有备选方案一致。

4.2. 渐近理论的有效性
接下来，让我们数值研究当X和Y独立时${\xi }_n(X,Y)$的分布。以$X_i$和$Y_i$为独立均匀[0，1]随机变量，n=20，生成了1万个${\xi }_n(X,Y)$值。$\sqrt{n}{\xi }_n(X,Y)$的直方图如下图所示，与定理2.1预测的渐近密度函数叠加。我们已经看到，对于n=20，符合程度是惊人的。

4.3. 功效和运行时长比较
在本节中，我们比较了基于${\xi }_n(X,Y)$的独立性测试与近年来提出的一些强大测试的威力，并比较了这些测试的运行时间。主要发现是，如果信号相对平稳，${\xi }_n(X,Y)$的强度比其他一些测试要小，如果信号摆动，${\xi }_n(X,Y)$的强度更大。就运行时间而言，${\xi }_n(X,Y)$具有很大的优势，因为它可以在时间$\mathcal{O}(n\log n)$中计算，而它的竞争对手需要时间$\mathcal{O}(n^2)$。通过数值例子进一步验证了这一点，数值例子表明，如果样本量在数千个左右，${\xi }_n(X,Y)$基本上是在合理时间内可以计算的唯一统计。

为了测试独立性，将与以下流行的测试统计量进行比较。我排除了太新的统计量（因为它们没有经过时间测试，在许多情况下软件不可用）或太旧的统计量（因为它们被更新的方法取代）。在以下$(X_1,Y_1),...,(X_n,Y_n)$是$R^2$上某个分布的i.i.d.样本。

进行对比的测试（统计量）：

• 最大信息系数（MIC）
• 距离相关性（Distance correlation）
• HHG测试
• 希尔伯特-施密特独立性准则（HSIC）

上述所有测试方法在温和条件下测试独立性是一致的。

在样本量n=100的情况下进行功效比较。在每种情况下，使用500次模拟来估计功效。分别使用R软件包energy、minerva、HHG和dHSIC计算距离相关、MIC、HHG和HSIC统计。从[−1, 1]上的均匀分布生成X，考虑了以下六种备选方案：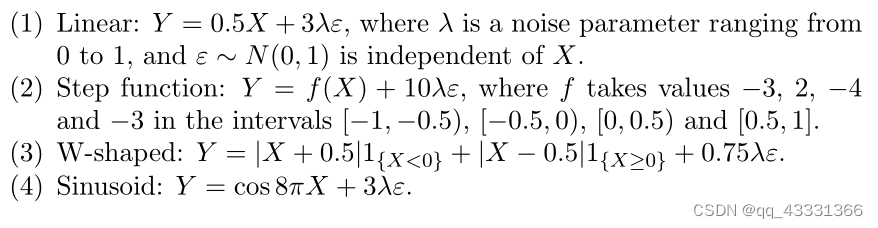

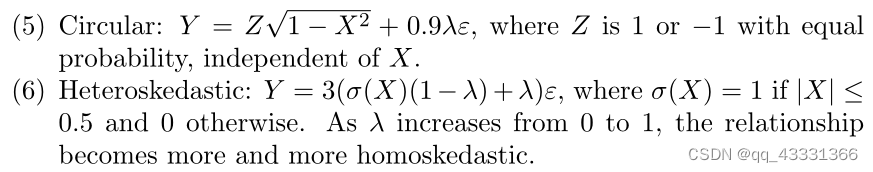
选择上述所有参数中的系数，以确保在λ从0到1变化时观察到完整的功效范围。结果如下图所示。该图的主要观察结果是，当信号具有振荡性质时，例如对于W形散点图和正弦曲线，${\xi }_n$比其他测试更强大。对于阶跃函数，它的表现也很好。然而，${\xi }_n$对于更平滑的备选方案，即线性、圆形和异方差散点图，性能较差。

接下来，让我们根据五个相互竞争的测试统计数据来比较独立性测试的运行时间。除${\xi }_n$外，测试独立性的唯一方法是进行置换测试。（HSIC有一个理论测试，但它只是一个粗略的近似值。）排列的数量被认为是最小的值得尊敬的数字，200。通常200对于置换测试来说太小了，但我认为它太小了，以至于对于较大的n值，程序会在一段可管理的时间内终止。对于${\xi }_n$，使用渐近测试，因为它在非常小的样本中与置换测试效果相当。

对于距离相关、HSIC和HHG，置换测试可直接从相应的R软件包中获得。对于MIC，我必须编写代码，因为程序包中不会自动提供置换测试，所以使用更好的代码可能会在一定程度上改善运行时间。对于HHG测试，该函数要求将X和Y的距离矩阵作为参数输入。为了公平起见，计算距离矩阵所需的时间包含在执行置换测试的总时间中。

结果如表2所示。对于所有样本量大于等于500的样本，每次测试都比基于ξn的测试慢数百倍甚至数千倍。对于样本量10000，HHG测试在30分钟内未收敛后终止。

最后作者总结了该方法的优缺点。
相对于上述所有优点，${\xi }_n$只有一个缺点：当信号平滑且无振荡时，它的功率似乎比几种流行的独立性测试要小。尽管此类信号包括实践中观察到的大多数类型，但只有当样本量较小时，这才是一个值得关注的问题。在大样本中，所有测试都很强大，计算时间成为一个更大的问题。