一。实验目的

预测信号由二阶线性预测模型产生，x(n)=v(n)+a1x(n-1)+a2x(n-2) .其中 v(n)是均值为零，方差为1的高斯白噪声序列，a1=1.558,a2=-0.81。分别利用LMS算法、格型LMS算法、RLS算法、LSL算法来估计线性预测模型参数a1和a2。

二。实验原理

2.1 LMS算法

LMS(Least mean square)算法是最常见的自适应滤波算法。所谓自适应滤波，就是利用前一个样本已获得的滤波器参数等结果，自动地调节下一时刻的滤波器参数，以适应信号和噪声未知的或随机变化的特性。LMS算法采用平方误差最小的准则代替均方误差最小的准则，信号的基本关系如下：
在这里插入图片描述
写成矩阵形式为：

在式2-1中，w(n)为第n时刻自适应滤波器的权矢量，N为自适应滤波器的阶数。X(n)为第n时刻自适应滤波器的参考输入矢量，由前N个信号采样值构成。d(n)是期望输出值，它通常是原始信号。e(n)为自适应滤波器的估计误差，是控制LMS算法收敛性和稳定度的常数，称作收敛因子。值的选取必须满足收敛条件。在收敛范围内，越大收敛效果越好，但过大，收敛过程将出现震荡。
根据以上分析，我们可以得到LMS算法的步骤如下：
在这里插入图片描述
(5)计算到第N-1时刻的滤波器系数，重复步骤(2)-(4)。

2.2 格型LMS算法

格型LMS算法结构如图：
在这里插入图片描述
其中：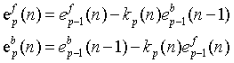

格型LMS算法原理框图如图：

2.3 RLS算法

RLS(Recursive least squares)算法即递归最小二乘法，是最小二乘算法的一类快速算法。递归最小二乘自适应滤波器是对一组已知数据的最佳滤波器，处理过程中没有对输入序列的统计特性做出假定，而是纯决定性的最小化问题。相对于LMS自适应滤波器具有更好的性能。RLS算法是用二乘方的时间平均的最小优化准则取代最小均方准则，并按时间进行迭代计算。算法流程大致如下：
算法初始化：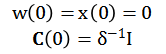
在这里插入图片描述
其中：

对每一时刻，n=1，2,…计算：

在上式中，"Lamda"称为遗忘因子，它是不超过1 的正数。d(n)为参考信号或期望信号，w(n)为第n次迭代的权值。
RLS算法的优点是收敛速度较快，而且适用于平稳信号的自适应处理。但是在每次迭代需要输入信号和参考信号，计算比较复杂。

2.4 LSL算法

自适应算法的目标在于，使滤波器输出与期望信号的误差平方统计平均值最小。这个准则根据输入数据的长期统计特性寻求最佳滤波。然而，我们通常已知的仅是一组数据，因而只能对长期统计特性进行估计或近似。例如LMS算法、格形LMS算法。而LSL算法能直接根据一组数据寻求最佳。LSL（Least square of lattice）是最小二乘格型算法，它由第M阶滤波器参数计算M+1阶滤波器参数。通常说来，移动环境是时变的，向量必须周期性地更新或自适应，每次更新计算的权值向量通常相对上一次计算的权值向量只有很小的变化。而且，由于估计最优解所需的数据受到噪声的污染，需要对权向量的上一个解进行更新，以平滑对最优响应的估计，减小噪声的影响。
LSL算法流程大致如下：
算法初始条件：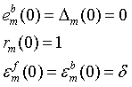
在这里插入图片描述
迭代运算，按时间n=1, 2, …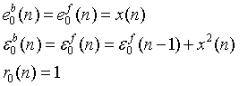

三、实验过程及仿真

二阶线性预测(AR2)模型原理框图如图所示。现在分别利用LMS算法、格型LMS算法、RLS算法、LSL算法来估计线性预测模型参数a1和a2。让自适应滤波器的权值收敛于a1,a2。最终比较四种算法的结果。
在这里插入图片描述
高斯白噪声v(n)用Matlab里的randn函数产生均值为0、方差为1的标准正态分布随机噪声来实现。随后的产生的信号用题目中的(AR2)模型产生，激励源是之前产生的高斯白噪声。信号点数这里取为1000，用1000个信号来估计滤波器系数。
仿真过程按照如下过程进行
（1）信号产生：首先产生高斯白噪声序列(n)，然后将此通过一个简单的二阶自回归滤波器生成信号x(n)，该滤波器的参数为a1=1.558,a2=-0.81；
（2）将步骤（1）生成的信号分别通过LMS、格型LMS、RLS、LSL自适应滤波器进行处理；
（3）通过改变u值收敛速度的影响来分析LMS算法、格型LMS算法、LSL算法的性能。通过改变值对收敛速度的影响来分析RLS算法的性能。
（4）绘制各种图形曲线，分析结果。

3.1 LMS算法仿真

为了分析算法性能，可以取3个不同的值，来比较不同收敛因子对算法收敛性和平稳性的影响。这里u值分别取0.001，0.002，0.004。根据2.1小节中LMS的基本原理和流程，在Matlab中编写LMS算法的程序。核心代码如下：

clc;
close all;
a1=1.558;a2=-0.81;%权初值
L=1000;      %信号点数
v=randn(1,L);%产生高斯白噪声,均值为0，方差为1
x=zeros(1,L);%初始化滤波器输入矢量
Y=zeros(1,L);%初始化滤波器实际输出的估计值
w1=zeros(1,L);%初始化滤波器系数
w2=zeros(1,L);
e=x;        %初始化估计误差
u=0.001;    %步长因子
x(1)=v(1);  %输入初始值
x(2)=a1*x(1)+v(2);
for n=3:L                 %L为信号长度
    x(n)=a1*x(n-1)+a2*x(n-2)+v(n);  %第n时刻的输入
    Y(n)=w1(n)*x(n-1)+w2(n)*x(n-2); %第n时刻的输出
    e(n)=x(n)-Y(n);               %误差信号
    w1(n+1)=w1(n)+2*u*e(n)*x(n-1);%w1,w2为滤波器系数.w1用来预测a1
    w2(n+1)=w2(n)+2*u*e(n)*x(n-2);%w2用来预测a2
end
figure(1);
plot(w1,'b');
hold on;        %在同一个图里绘制多个曲线
plot(w2,'r');
xlabel('n');
ylabel('权值变化');
title(['LMS算法实现线性预测,收敛因子u=',num2str(u)]);
plot([1,n],[a1,a1],'y');    %画出a1,a2两条水平线，便于比较
plot([1,n],[a2,a2],'g');
legend('w1','w2','a1=1.558','a2=-0.81');
grid on;        %开启坐标网格

3.2 格型LMS算法仿真

按照同样的方法，取3个不同的值，来比较不同收敛因子对算法收敛性和平稳性的影响。这里u值分别取0.001，0.002，0.004。格型LMS算法代码如下：

%格型LMS算法自适应滤波器收敛性仿真实验
clc;                      % 清除指令窗显示的内容；
close all;                  % 关掉当前的图像窗口
a1=1.558;                 % 初始化二阶线性预测滤波器的系数
a2=-0.81;                 % 初始化二阶线性预测滤波器的系数
L=1024;                  % 信号的长度
v=randn(1,L);              % 产生噪声信号作为线性预测滤波器输入信号；
x=zeros(1,L);
x(1)=v(1);					%输入初始值
x(2)=a1*x(1)+v(2);
u=0.001;                 	% 步长因子
% 前向线性预测滤波器
for i=3:L                       
    x(i)=a1*x(i-1)+a2*x(i-2)+v(i);     % 产生自适应滤波器的输入信号x(n)；
end
%初始化各系数
ef = zeros(3,L);                     % 格型LMS滤波器前向预测误差矩阵;
                                  % 第一至第三行分别对应ef0,ef1,ef2;
eb = zeros(3,L);                     % 格型LMS滤波器后向预测误差矩阵;
                                  % 第一至第三行分别对应eb0,eb1,eb2.
ef(1,:)=x;
eb(1,:)=x;
k=zeros(3,L+1);                      % 其中第2、3行为有效数值；
                                   % 加第一行是为了编程方便。                 
w1=zeros(1,L+1);
w2=zeros(1,L+1);
w1(1)=0;
w2(1)=0;
% 计算出格型LMS滤波器的前后向预测误差
for n=2:L           %L为信号的长度
    for p=2:3
        ef(p,n)=ef(p-1,n)-k(p,n)*eb(p-1,n-1);
        eb(p,n)=eb(p-1,n-1)-k(p,n)*ef(p-1,n);
        k(p,n+1)=k(p,n)+2*u*(ef(p,n)*eb(p-1,n-1)+eb(p,n)*ef(p-1,n));  
    end
    w1(n+1)=k(2,n+1)*(1-k(3,n+1));% 计算出前向AR线性预测滤波器权系数的估计值
    w2(n+1)=k(3,n+1);
end
% 绘图输出
figure (1);
hold on;				%在同一个图里绘制多个曲线
plot(w1,'b');
plot(w2,'r');
plot([1,n],[a1,a1],'y');	%画出a1,a2两条水平线，便于比较
plot([1,n],[a2,a2],'g');
grid on;
axis tight;
s=legend('w1','w2','a1=1.558','a2.-0.81');
set(s,'Location','East');%把图例放在图的右边中间，方便观察
xlabel('n');
ylabel('权值变化');
title(['LLMS算法实现线性预测,其中u=',num2str(u)]);

3.3 RLS算法仿真

根据二阶线性预测模型框图以及RLS算法的基本原理，在Matlab编写相应的RLS程序。通过改变值对收敛速度的影响来分析RLS算法的性能。在本程序中，Lamda分别取1，0.998，0.996。

%预测信号由2阶AR模型产生,用LMS算法估计模型参数a1，a2
clc;% 清除命令窗口显示的内容
a1=1.558;a2=-0.81;%权初值
n=2000; %信号点数
x=zeros(1,n)';%预分配内存
y=zeros(1,n);
e=zeros(1,n);
w=randn(1,n)';
x(1)=w(1);
x(2)=a1*x(1)+w(2);
for i=3:n
    x(i)=w(i)+a1*x(i-1)+a2*x(i-2);
end
L=2;%滤波器长度
lam=0.999;  %指数加权因子
WR=zeros(L,n);%权矢量更新值
T=eye(L,L)*10;%RLS算法T参数的初始化,T=10
for i=(L+1):n
    X=x(i-1:-1:(i-L));%延时函数
    %X=[x(n-1);x(n-2)];
    K=(T*X)/(lam+X'*T*X);%i时刻增益值
    e1=x(i)-WR(:,i-1)'*X;
    WR(:,i)=WR(:,i-1)+K*e1;%i时刻权值
    y(i)=WR(:,i)'*X;%i时刻输出
    e(i)=x(i)-y(i);%预测误差
    T=(T-K*X'*T)/lam;%i时刻的维纳解
end
a1R=WR(1,1:n);%a1在RLS算法下的变化
a2R=WR(2,1:n);%a2在RLS算法下的变化
figure;
plot(1:n,a1R,'blue');
hold ;
plot(1:n,a2R,'black');
plot([1,n],[a1,a1],'y');
plot([1,n],[a2,a2],'g');
grid on;
s=legend('a1R','a2R',['a1=',num2str(a1)],['a2=',num2str(a2)]);
xlabel('n-信号点数');
ylabel('权值变化');
title(['递归最小二乘（RLS）算法权调整曲线图,lam=',num2str(lam)]);
set(s,'Location','East');		%把图例放在图的右边中间，方便观察

3.4 LSL算法仿真

根据二阶线性预测模型框图以及RLS算法的基本原理，在Matlab编写相应的RLS程序。通过改变前后向预测误差相关系数初值γ对收敛速度的影响，进而分析算法性能。在本程序中，γ分别取0.98，1.00，1.02。

clc;
clear;
N=1024;		%信号点数
M=3;		%滤波器阶数
a1=1.558;	%线性预测值
a2=-0.81;
kf=zeros(M,N);
kb=zeros(M,N);
wl=zeros(1,N);
w2=zeros(1,N);
ef=zeros(M,N);
eb=zeros(M,N);
delta=zeros(M,N);
dd=1.00;
epf=dd*ones(M,N);
epb=dd*ones(M,N);
gma=ones(M,N);
x=randn(1,N);
xu(1)=x(1);
xu(2)=a1*xu(1)+x(2);
for n=3:N
    xu(n)=x(n)+a1*xu(n-1)+a2*xu(n-2);%第n时刻的输入
end
for n=2:N                   		%按时间迭代计算
    eb(1,n)=xu(n-1);              %eb为前向线性预测误差
    ef(1,n)=xu(n-1);              %ef为后向线性预测误差
    epb(1,n)=epf(1,n-1)+xu(n-1)^2;%epb为前向预测误差功率
    epf(1,n)=epf(1,n-1)+xu (n-1)^2;%epf后向预测误差功率
    gma(1,n)=0.98;               %前后相预测误差相关系数
for m=2:3                   		%按阶数迭代计算
    delta(m,n)=delta(m,n-1)+eb(m-1,n-1)*ef(m-1,n)/gma(m-1,n);
    ef(m,n)=ef(m-1,n)-delta(m,n)*eb(m-1,n-1)/epb(m-1,n-1);
    eb(m,n)=eb(m-1,n-1)-delta(m,n)*ef (m-1,n)/epf(m-1,n);
    epf(m,n)=epf(m-1,n)-delta(m,n)^2/epb(m-1,n-1);
    epb(m,n)=epb(m-1,n-1)-delta(m,n)^2/epf(m-1,n);
    gma(m,n-1)=gma(m-1,n-1)-eb(m-1,n-1)^2/epb(m-1,n-1);
    kf(m,n)=delta(m,n)/epf(m-1,n);  %kf为前向预测误差功率
    kb(m,n)=delta(m,n)/epb(m-1,n-1);%kb后向预测误差功率
end
    w1(n)=kb(2,n)-kf(2,n)*kb(3,n);  %更新滤波器权系数
    w2(n)=kb(3,n);
end
figure(1);
plot(w1,'r','linewidth',2);
hold on;
plot(w2,'b','linewidth',2);
grid on;
plot([1,n],[a1,a1],'y');
plot([1,n],[a2,a2],'g');
xlabel('n');
ylabel('权值变化');
title('LSL算法实现线性预测');
s=legend('w1','w2',['a1=',num2str(a1)],['a2=',num2str(a2)]);
set(s,'Location','East');

四.仿真结果及分析

图4-1到4-3为LMS算法仿真二阶线性预测模型的结果。每个图的两条曲线是滤波器的权值w1,w2随着信号点数变化。当u=0.001时，曲线收敛速度很慢，快接近信号末尾才收敛，但是曲线比较平稳。而当u=0.004时，收敛速度快，但是曲线平稳性差。在选择步长时，稳态误差和收敛速度之间是相互矛盾的：步长越小，稳态误差越小，收敛速度慢；步长越大，收敛速度越快，收敛后的稳态误差也越大。
图4-1
图4-2
图4-3
图4-4到4-6为LMS算法仿真二阶线性预测模型的结果。每个图的两条曲线是格型LMS滤波器的权值w1,w2随着信号点数变化。很明显，两条曲线变化的形状与图4-1到4-3的曲线图变化形状相似。但是，在相同的u值下，格型LMS滤波器的权值收敛速度大于LMS滤波器的权值收敛速度。因此，格型LMS滤波器比LMS滤波器性能好。
图4-4
图4-5
图4-6
图4-7到4-9为LMS算法仿真二阶线性预测模型的结果。每个图的两条曲线是LSL滤波器的权值w1,w2随着信号点数变化。在相同的u值下，LSL滤波器的权值收敛速度比LMS滤波器和格型LMS滤波器的权值收敛速度都快。因此，LSL滤波器的性能比格型LMS滤波器和LMS滤波器要好。
图4-7
图4-8
图4-9
图4-10到4-12为RLS算法仿真二阶线性预测模型的结果。通过改变值对收敛速度的影响来分析RLS算法的性能。在本程序中，Lamda分别取1，0.998，0.996。根据运行结果，指数加权因子Lamda越接近1时，算法的收敛特性和平稳性越好。
t图4-10
图4-11
图4-12