原理

今天介绍另一种十分高效的排序算法——归并排序。其通过将两个有序的表合并成一个有序表进行排序，过程是取两个待合并数组$A$和$B$，一个待输出数组$C$，以及计数器$Actr$、$Bctr$、$Cctr$，计数器初始位置于其数组首地址，然后将$Actr$和$Bctr$指向值中的最小值赋予$Cctr$，相关计数器各向前进一位，重复操作，当数组$A$和$B$中一个用完时，将另一个剩余部分复制至数组$C$中。如下图。

这里有一个问题，那就是待排序的表不一定是由若干个有序的子表组成，如{ 50, 10, 90, 30, 70, 40, 80, 60, 20}。其实任意表都是由若干有序子表构成，见下图

我们先将这个无序表分成两个子表，发现并不是各自有序的，我们对两个子表继续分。

我们将左部分继续分直至每个子表只含一个元素，此时表便是有序的，然后两两合并。右半部分同理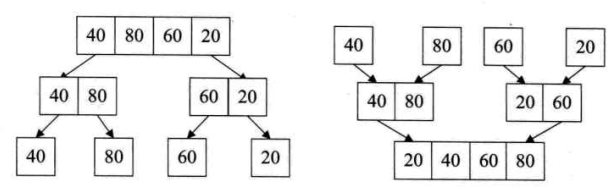

最后合并两个子表。

上述其实使用了递归的思想，先“从上往下”拆分，再“从下往上”合并。如果大家对递归理解深刻的话，其过程如下。

所以我们可知使用递归的方法很方便的写出代码。

代码实现

因为不需要哨兵，所以不再使用之前定义的结构体，使用容器$vector$。

void Merge(vector<int>& numbers, int start, int mid, int end) 
{
	int* temp = new int[end - start + 1];	//第一步，申请空间，大小为两个排序序列之和
	int fistSectionIndex = start;			//第二步，设定两个待排序列的起始位置的索引
	int secondSectionIndex = mid + 1;
	int tempIndex = 0;	//所申请空间的索引

	while (fistSectionIndex <= mid && secondSectionIndex <= end) //直到两个序列中有一个到达终止位置
	{	
		if (numbers[fistSectionIndex] <= numbers[secondSectionIndex])
			temp[tempIndex++] = numbers[fistSectionIndex++];
		else
			temp[tempIndex++] = numbers[secondSectionIndex++];
	}

	while (fistSectionIndex <= mid)
		temp[tempIndex++] = numbers[fistSectionIndex++];

	while (secondSectionIndex <= end)
		temp[tempIndex++] = numbers[secondSectionIndex++];

	for (int j = 0; j < tempIndex; ++j)		//将合并且排序好的元素，复制到原来的数组中，释放临时数组空间
		numbers[start + j] = temp[j];

	delete[] temp;
}


void MergeSort(vector<int>& numbers, int start, int end) 
{
	if (numbers.empty() || start >= end)
		return;

	int mid = (start + end) / 2;

	MergeSort(numbers, start, mid);		//递归排序numbers[start,mid](首先从上往下递归分解到最底层元素个数为1的情况)
	MergeSort(numbers, mid + 1, end);	//递归排序numbers[mid + 1,end](首先从上往下递归分解到最底层元素个数为1的情况)

	Merge(numbers, start, mid, end);	//然后递归的从下往上合并排序
}

void MergeSort(vector<int>& numbers)    //重载外部接口
{
	MergeSort(numbers, 0, numbers.size() - 1);
}

递归都可以使用迭代实现，归并算法的迭代实现代码见：https://github.com/kfcyh/sort/tree/master/mergesort

性能分析

归并排序的最好、最坏和平均的时间复杂度都为$O(nlogn)$，因为它需要进行元素的两两比较所以不存在跳跃，所以归并排序是稳定的排序算法，但递归实现的归并排序需要的额外空间比较大，而迭代实现则相对较小，运行时间开销也较小，因此应尽量使用迭代方法。