程序基本算法习题解析用分治法求a^n。

题目：

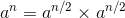
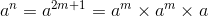
如果n为偶数，则 $a^{^{n}}=a^{^{n/2}}\times a^{^{n/2}}$ ；如果n为奇数，则 $a^{^{n}}=a^{^{2m+1}}=a^{^{m}}\times a^{^{m}}\times a$ ，其中m为偶数。

思路不难，直接附上代码：

// Chapter7_7.cpp : Defines the entry point for the application.
// 用分治法求a^n。

#include "stdafx.h"
#include<iostream>
using namespace std;

int funPower(int a,int n) //a^n
{
	if(n == 1)
		return a;
	else
	{
		//如果n为偶数
		if(n%2 == 0)
			return funPower(a,n/2)*funPower(a,n/2);
		//如果n为奇数
		else
			return funPower(a,n/2)*funPower(a,n/2+1);
	}
}
int main()
{
	int result,a,n;
	cout << "input a,n: ";
	cin >> a >> n;
	result = funPower(a,n);
	cout << a << "的" << n << "次方为：" << result << endl;
	system("pause");
	return 0;
}

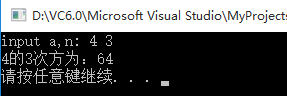
运行结果为：

原文链接：https://blog.csdn.net/elma_tww/article/details/85052650