62.不同路径 (1)
解题思路:在如图3*7的网格中:要从星号的位置走到星号的位置,通过一条一条数发现有28条路径。
如题目中所描述的,机器人只能向右走和向下走,所以将网格中第一行和第一列位置都置为1,然后其它位置是其上方和左方的数字之和。
C代码如下:
int uniquePaths(int m, int n)
{
int arr[m][n];
for(int i=0;i<m;i++)
{
for(int j=0;j<n;j++)
{
arr[i][0]=arr[0][j]=1;
}
}
for(int i=1;i<m;i++)
{
for(int j=1;j<n;j++)
{
arr[i][j]=arr[i-1][j]+arr[i][j-1];
}
}
return arr[m-1][n-1];
}
1658. 将X减到0的最小操作数 (2)
给你一个整数数组 nums 和一个整数 x 。每一次操作时,你应当移除数组 nums 最左边或最右边的元素,然后从 x 中减去该元素的值。请注意,需要 修改 数组以供接下来的操作使用。
如果可以将 x 恰好 减到 0 ,返回 最小操作数 ;否则,返回 -1 。
示例 1:
输入:nums = [1,1,4,2,3], x = 5 输出:2
解释:最佳解决方案是移除后两个元素,将 x 减到 0 。
示例 2:
输入:nums = [5,6,7,8,9], x = 4 输出:-1
示例 3:
输入:nums = [3,2,20,1,1,3], x = 10 输出:5
解释:最佳解决方案是移除后三个元素和前两个元素(总共 5 次操作),将 x 减到 0 。
C代码:
int minOperations(int* ar, int n, int x)
{
int Sum = 0;
for (int i = 0; i < n; i++)
{
Sum += ar[i];
}
int target = Sum - x;
int left = 0;
int right = 0;
int count = 0;
int step = -1;
if (target == 0)
{
return n;
}
if (target < 0)
{
return -1;
}
while (right < n)
{
if(count < target)
{
count += ar[right];
right++;
}
if (count > target)
{
count -= ar[left++];
}
if (count == target)
{
int tmp = right - left;
//此时tmp的值会不断赋值改变,所以通过移动可以找到最优的解
step = step > tmp ? step : tmp;
count -= ar[left++];//控制窗口向右移动
}
}
if (step == -1)
{
return -1;
}
return n-step;
}
8. 字符串转换整数 (atoi)(3)
请你来实现一个 myAtoi(string s) 函数,使其能将字符串转换成一个 32 位有符号整数(类似 C/C++ 中的 atoi 函数)。
函数 myAtoi(string s) 的算法如下: 读入字符串并丢弃无用的前导空格
检查下一个字符(假设还未到字符末尾)为正还是负号,读取该字符(如果有)。 确定最终结果是负数还是正数。 如果两者都不存在,则假定结果为正。
读入下一个字符,直到到达下一个非数字字符或到达输入的结尾。字符串的其余部分将被忽略。
将前面步骤读入的这些数字转换为整数(即,“123” -> 123, “0032” -> 32)。如果没有读入数字,则整数为 0 。必要时更改符号(从步骤 2 开始)。
如果整数数超过 32 位有符号整数范围 [−231, 231 − 1] ,需要截断这个整数,使其保持在这个范围内。具体来说,小于 −231 的整数应该被固定为 −231 ,大于 231 − 1 的整数应该被固定为 231 − 1 。
返回整数作为最终结果。
示例 1:
输入:s = “42” 输出:42
解释:加粗的字符串为已经读入的字符,插入符号是当前读取的字符。
第 1 步:“42”(当前没有读入字符,因为没有前导空格)
第 2 步:“42”(当前没有读入字符,因为这里不存在 ‘-’ 或者 ‘+’)
第 3 步:“42”(读入 “42”)
解析得到整数 42 。 由于 “42” 在范围 [-231, 231 - 1] 内,最终结果为 42 。
示例 2:
输入:s = " -42" 输出:-42
解释:
第 1 步:" -42"(读入前导空格,但忽视掉)
第 2 步:" -42"(读入 ‘-’ 字符,所以结果应该是负数)
第 3 步:" -42"(读入 “42”)
解析得到整数 -42 。 由于 “-42” 在范围 [-231, 231 - 1] 内,最终结果为 -42 。
示例 3:
输入:s = “4193 with words” 输出:4193
解释:
第 1 步:“4193 with words”(当前没有读入字符,因为没有前导空格)
第 2 步:“4193 with words”(当前没有读入字符,因为这里不存在 ‘-’ 或者 ‘+’)
第 3 步:“4193 with words”(读入 “4193”;由于下一个字符不是一个数字,所以读入停止)
解析得到整数 4193 。 由于 “4193” 在范围 [-231, 231 - 1] 内,最终结果为 4193 。
示例 4:
输入:s = “words and 987” 输出:0
解释:
第 1 步:“words and 987”(当前没有读入字符,因为没有前导空格)
第 2 步:“words and 987”(当前没有读入字符,因为这里不存在 ‘-’ 或者 ‘+’)
第 3 步:“words and 987”(由于当前字符 ‘w’ 不是一个数字,所以读入停止)
解析得到整数 0 ,因为没有读入任何数字。 由于 0 在范围 [-231, 231 - 1] 内,最终结果为 0 。
示例 5:
输入:s = “-91283472332” 输出:-2147483648
解释:
第 1 步:"-91283472332"(当前没有读入字符,因为没有前导空格)
第 2 步:"-91283472332"(读入 ‘-’ 字符,所以结果应该是负数)
第 3 步:"-91283472332"(读入 “91283472332”)
解析得到整数 -91283472332 。
由于 -91283472332 小于范围 [-231, 231 - 1] 的下界,最终结果被截断为 -231 = -2147483648 。
C代码如下:
int myAtoi(char * s)
{
int i=0;
long double num=0;
int len=strlen(s);
int tag=1;
while(*s==' ')
{
s++;
len--;
}
if(*s=='-')
{
tag=-1;
s++;
len--;
}
else if(*s=='+')
{
s++;
len--;
}
int *newnum=(int*)malloc(sizeof(int)*len);
while(*s!='\0')
{
newnum[i]=(int)*s-48; //将每一个符号都转换为数字
if(newnum[i]<0||newnum[i]>9)
{
break;
}
num=num*10+newnum[i];
i++;
s++;
}
if(num*tag<=-2147483648)
{
return -2147483648;
}
if(num*tag>=2147483647)
{
return 2147483647;
}
else
{
return num*tag;
}
}
866. 回文素数(求出大于或等于 N 的最小回文素数)(4)
回顾一下,如果一个数大于 1,且其因数只有 1 和它自身,那么这个数是素数。 例如,2,3,5,7,11 以及 13 是素数。
回顾一下,如果一个数从左往右读与从右往左读是一样的,那么这个数是回文数。 例如,12321 是回文数。
示例 1: 输入:6
输出:7
示例 2: 输入:8
输出:11
示例 3: 输入:13
输出:101
法一:超时但逻辑是对的,再一定范围内也可以运行:(超时了)
bool IsPrime(int m)
{
if (m == 1)
{
return false;
}
if (m == 2)
{
return true;
}
for (int i = 2; i * i <= m; i++)
{
if (m % i == 0)
{
return false;
}
}
return true;
}
bool IsPalindrome(int k)
{
int ar[10] = { 0 };
int i;
for (i = 0; k != 0; i++)
{
ar[i] = k % 10;
k = k / 10;
}
int j = 0;
int h = i - 1;
while (j < h)
{
if (ar[j] == ar[h])
{
j++;
h--;
}
else
{
return false;
}
}
return true;
}
int primePalindrome(int n) //英文表示回文素数
{
while (1)
{
if( n % 2 == 1 || n ==2)
{
if (IsPrime(n) && IsPalindrome(n))
{
return n;
}
}
n++;
}
}
278. 第一个错误的版本(5)
你是产品经理,目前正在带领一个团队开发新的产品。不幸的是,你的产品的最新版本没有通过质量检测。由于每个版本都是基于之前的版本开发的,所以错误的版本之后的所有版本都是错的。
假设你有 n 个版本 [1, 2, …, n],你想找出导致之后所有版本出错的第一个错误的版本。
你可以通过调用 bool isBadVersion(version) 接口来判断版本号 version 是否在单元测试中出错。实现一个函数来查找第一个错误的版本。你应该尽量减少对调用 API 的次数。
示例:
给定 n = 5,并且 version = 4 是第一个错误的版本。
调用 isBadVersion(3) -> false
调用 isBadVersion(5) -> true
调用 isBadVersion(4) -> true
所以,4 是第一个错误的版本。
// The API isBadVersion is defined for you.
// bool isBadVersion(int version);
class Solution
{
public:
int firstBadVersion(int n)
{
int left=0,right=n;
int mid;
while(left<=right)
{
mid=left+(right-left)/2; //这一步非常重要,不能写 int mid = (left + right) / 2
if(!isBadVersion(mid))
{
left=mid+1;
}
else
{
right=mid-1;
}
}
return left;
}
};
不能写 int mid = (lo + hi) / 2 , 要写 int mid = lo + (hi - lo) / 2, 这个题目,返回left 或者 right 都行,因为终止条件是 lo == hi , 这是二分里比较难的题目了吧,找的是分割点,不是某个值。
LCP 28. 采购方案(6)
小力将 N 个零件的报价存于数组 nums。小力预算为 target,假定小力仅购买两个零件,要求购买零件的花费不超过预算,请问他有多少种采购方案。
注意:答案需要以 1e9 + 7 (1000000007) 为底取模,如:计算初始结果为:1000000008,请返回 1
示例 1:
输入:nums = [2,5,3,5], target = 6 输出:1 解释:预算内仅能购买 nums[0] 与 nums[2]。
示例 2:
输入:nums = [2,2,1,9], target = 10 输出:4
解释:符合预算的采购方案如下:
nums[0] + nums[1] = 4
nums[0] + nums[2] = 3
nums[1] + nums[2] = 3
nums[2] + nums[3] = 10
**解:题目分析:**如下图所示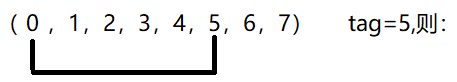
则0到5区间内的数都是符合规律的,虽然题目中的数字不一定是这样的大小,但是 left 和 right 都表示的是从 0 到 n 的下标,而0到5区间内却不止单单几种组合方法,光和0可以匹配的就有5中方案,所以先用right - left 将0后面的数依次与0单独匹配,再将left++,将1与1后面的数依次与1单独匹配,从而可以算出符号要求的总的方案。
class Solution {
public:
int purchasePlans(vector<int>& nums, int target)
{
int left,right;
long int n=0;
sort(nums.begin(),nums.end());
for(left=0,right=nums.size()-1;left<right;)
{
if(nums[left]+nums[right]>target) right--;
else
{
n=n+right-left;
left++;
}
}
return n%1000000007;
}
};