本文一共总结了凸包构造的四种算法:Incremental Construction、Jarvis步进法、Graham Scan和Divide-And-Conquer
一、Incremental Construction
就像插入排序一样,每次选一个不在凸包集合内的点加入,判断加入的点是否影响凸包极点(边界点)的size,若加入的点使得size变化或边界集合改变,则调整,如下图6,7,9所示。

1.In-Convex-Polygon Test:判定待定点是否位于某多边形内部
先对多边形进行一个“预处理”,给每个点按序编号,类比有序向量二分查找的思想,来逐步缩小规模。如下图:
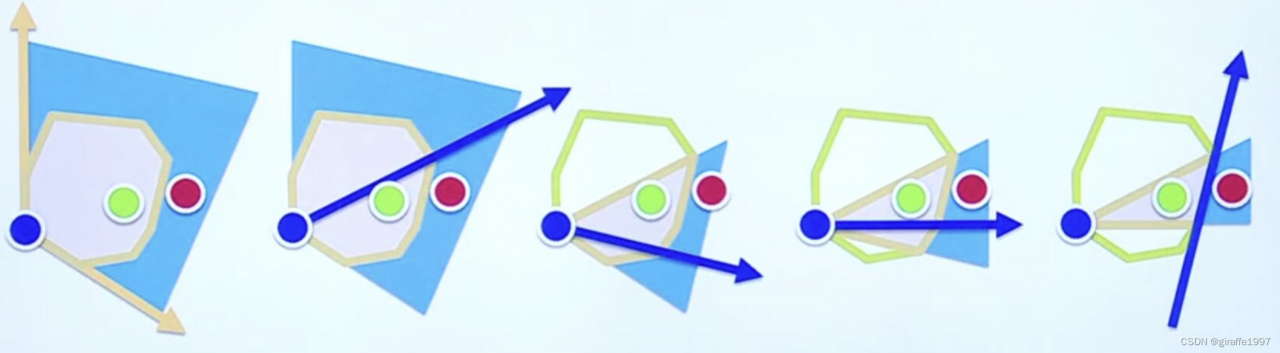
首先任选一点为基准点(蓝色点),然后用二分法选取其余点的“中点“(预处理已经为所有点排了序),然后判断基准点到终点的有向直线与待定点的位置关系(to-left test)。然后可将搜索范围减半,反复上述过程,直到最后退化为平凡情况:三角形与点的位置关系(in-triangle test)。
数学中「平凡」「退化」的含义?
- 平凡是指最简单的情形,或者说是容易证明的、容易看到的。
- 退化的事物就是在某种意义的等级或复杂程度上比一般情况更低的事物,可以是某种特殊,极限的情形。
整个算法共log(n)步,每步的to-left test或in-triangle test都为常数成本,则整体复杂度为log(n)。但是,每步都会将原凸包规模减半,且每加入一个极点,凸包的size都会发生改变。就像插入排序一样,每次插入都会改变原来的顺序,需要移动其他靠后的元素,即使使用了效率高的二分查找,对整体的复杂度没有影响,依然是O(n*n)。
判断点是否在凸包外部之后,就要把点加入到凸包集合中,若在外部还要调整凸包极点的size。
2.加入新点构造凸包
整个构造算法可以分成两大部分:
- 判断凸包与新点的位置关系(in-convex-polygon test)
- 向凸包插入新点
如下所示,X是位于凸包外的新点,由X出发,向每一个凸包边界点发出一条射线,对于点V,射线的to-left-test和to-right-test都为真,也就是V的前驱和后继节点分别位于两边。但是对于点T,S来说,to-left-test和to-right-test有一方为假,T,S就是V所要连接的点,他们重新构成极边,T到S之间的前驱/后继就成了凸包内的点。

3.结合1&2,将判断和加入新点结合在一起操作
再来回顾整个凸包构造算法的两大问题:in-convex-polygon test和插入新点。分开考虑只是为了将思路简化,实际上这两个问题可以套用一个算法,同时来解决:
对每个新点X,都遍历凸包的极点,然后对两点的射线进行to-left-test和to-right-test,当X在凸包外时,必然出现有极点的前驱的后继节点都在一侧的情况;当X在凸包内时,则不会出现上述情况。相应的也能找到对应的连接点。
综上,算法的复杂度为:(遍历凸包边界点N)*(to-left测试/to-right测试N)=O(N*N)
二、Jarvis步进法
此方法也用到了to-left-test,具体如下:
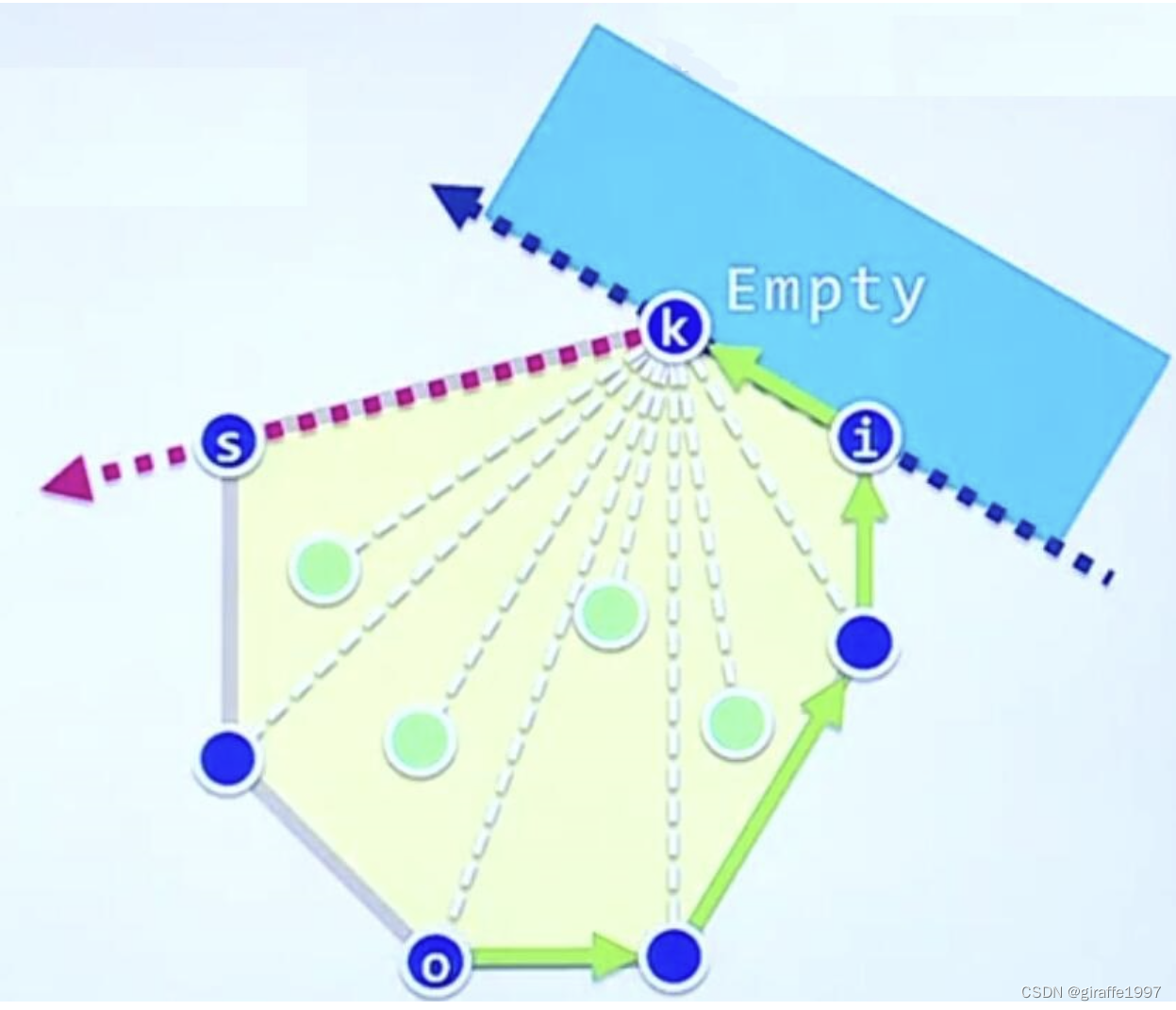
已知i已经是凸包边界节点,从i点到k点做一射线,可用看到所有的点都在极边ik的右侧,则K点是下一个边界节点。继续往下,随机找一个不在边界集合的点,假设为当前最左节点,遍历下一个不在边界集合的点时,和当前节点比较谁在更左侧,若是当前节点则继续往下遍历,否则更新此节点为更左的点,上图相对K最左的点是S,该方法可准确找到凸包极点。
算法步骤:
step1:首先确定第一个凸包极点,根据理论,设定点集中y最小的点为第一个,若存在y相同的多个点,则设定这些待定点中x最小的为第一个, 时间复杂度O(n)。
step2:以第一个点为基点(也就是参照),开始枚举每一个点非凸包点H′,找出点集中最逆时针方向的一个(利用叉积即可)为第二个极点,时间复杂度O(n)。
step3:以第二个点为基点重复step2, 直到找到的某点等于第一个点为止。
算法复杂度:
每次循环都会找到一个凸包上的点, 然后重复一次step2, 所以step2总共会进行H次(也就是凸包边界的个数), 所以时间复杂度O(H)∗O(n)=O(nH),也就是说该算法的复杂度受到凸包size的影响,若size很小则复杂度接近O(N),若size很大则接近O(N*N)。
PS:因为算法效率受到了输出的影响,故这样的算法称为 output sensitive algorithm
三、Graham Scan
该算法利用to-left-test和两个栈实现凸包计算:
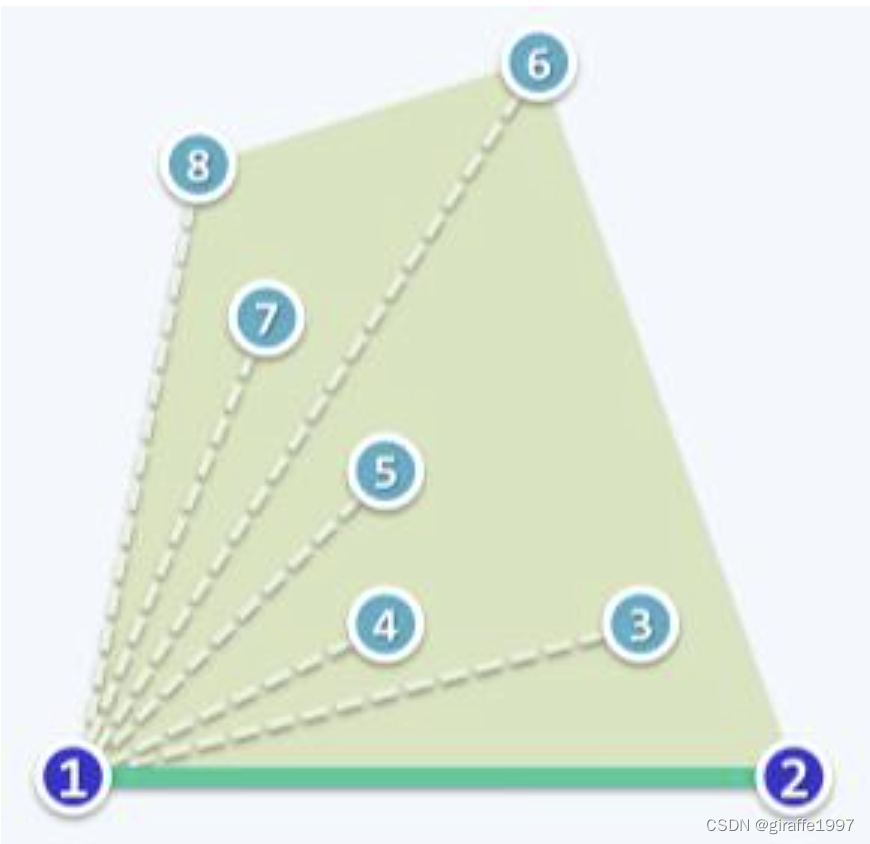
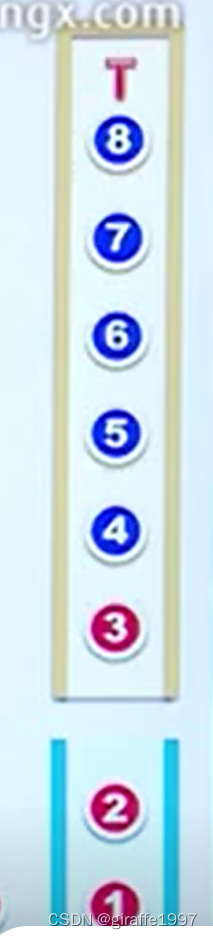
首先做排序预处理:和上面的方法一样,设定点集中y最小且处于左边的点为基准点,如点1,将其他点然后按照与1的连线与水平线1->2构成的夹角从小到大进行一次排序(最快O(NlogN)),按从大到小的顺序入栈T(上方的栈)。1和找到的夹角最小的顶点2入另一个栈S(下方的栈),这个栈存放最终的结果。除此之外,还需要3个指针,分别指向S的前两个栈顶元素(*s1,*s2),T的栈顶(*t1)。
算法步骤:
step1:若T栈非空,从栈顶开始遍历点,若*t1在边*s1*s2的左边,即to-lef-test为真,则把*t1指向的顶点出栈,并push进S。(例如上图中的3位于1、2两点左侧,入S栈)
step2:若to-lef-test为假,说明S栈的栈顶元素位于凸包的内部,则把*s1指向的元素出栈,*t1继续与下一个*s1*s2进行to-left-test,重复这一步直到测试结果为真(例如上图中的5位于S栈栈顶的顶点3、4的右侧,则4出栈,5继续和2、3测试,结果为真,入S栈)
step3:回到第一步,直到T为空。
算法复杂度:
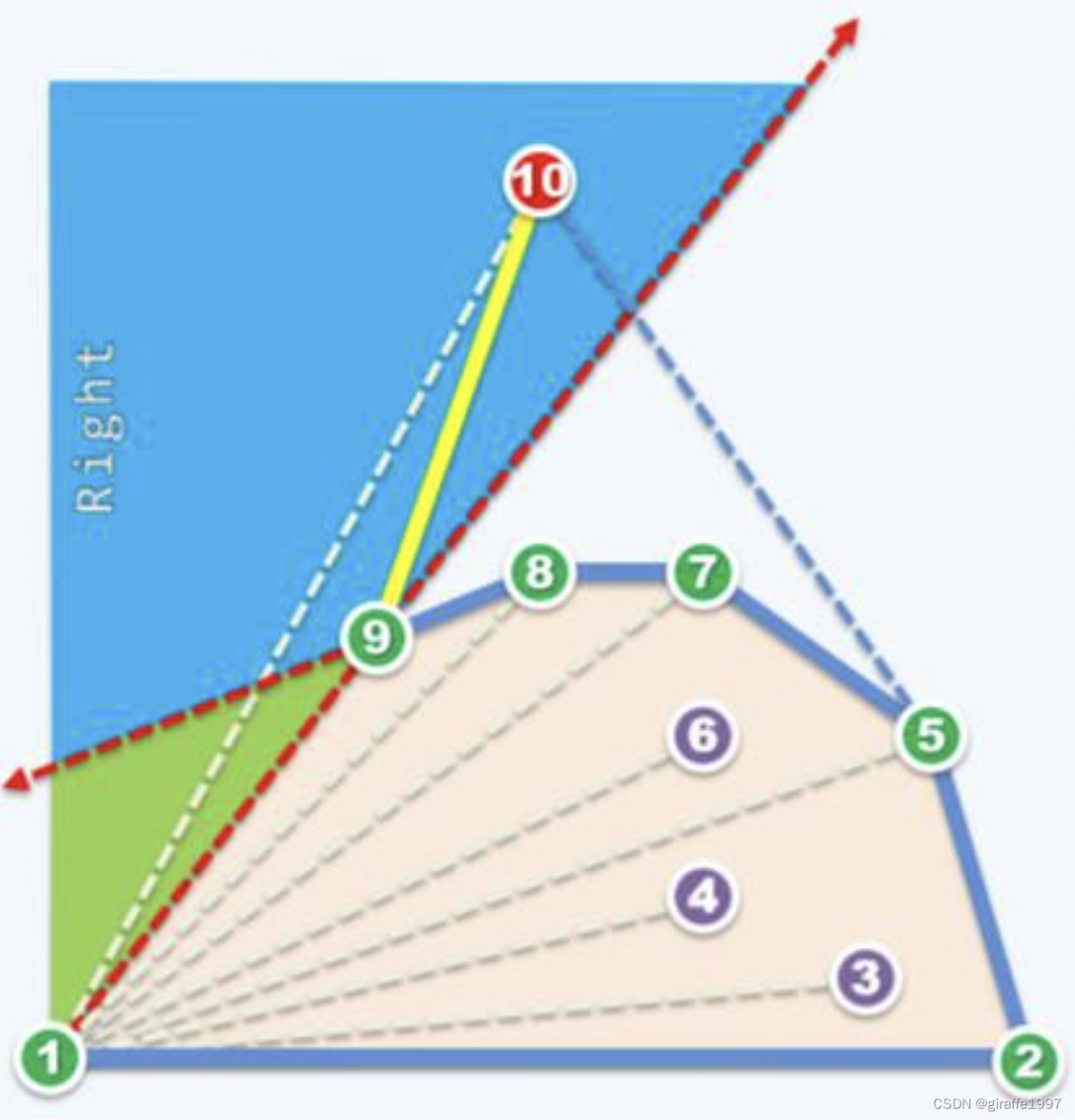
最后位于S栈中的所有顶点就是凸包极点。该算法几乎遍历了所有的顶点,加上每次都进行to-left-test然后出栈入栈(这一步称为scan),如上图所示,当10号点出栈时,点7,8,9与10的连线因为不位于上一个极边划分的空间的左边,需要回退3步,极端情况下,若每一个点的加入都要回退数步,该算法的性能则大大减少。
这样看来,好的时候复杂度能到O(N),坏的时候会达到O(N*K),而K的是否值会接近N?

所以回退的步数最大是多少?上图可以看到,黄色边是没有采纳的,就是to-left测试判定为false后直接丢弃的。紫色边则是曾经被认为是极边而接纳的,后来经过回溯又丢弃了,黄边和紫边的数量决定了找极边算法的复杂度。
通过观察可以发现,从图论的角度看,所有的黄色边和紫色边连在一起构成了一张平面图,也就是它们互相是不可能内部相交的。平面图有一个重要性质:
平面图中所有边的数目和顶点数目保持同阶
这个性质来自欧拉公式:
有n个点的平面图,边的数目上限是3n。
也就是说,出栈入栈遍历了所有的边的算法复杂度不会超过O(3N)。根据这个性质,在排序预处理之后的流程中,Graham Scan所能走过的所有边不仅不会到达N*N,而是顶多到达和顶点数N同阶的一个线性数目。
故算法复杂度主要受预处理影响,总体复杂度为O(NlogN)。
四、Divide-And-Conquer
算法沿着某一轴将点集划分为若干组,分别对每一组进行凸包算法(任一算法都可)得出子凸包,然后一一合并凸包
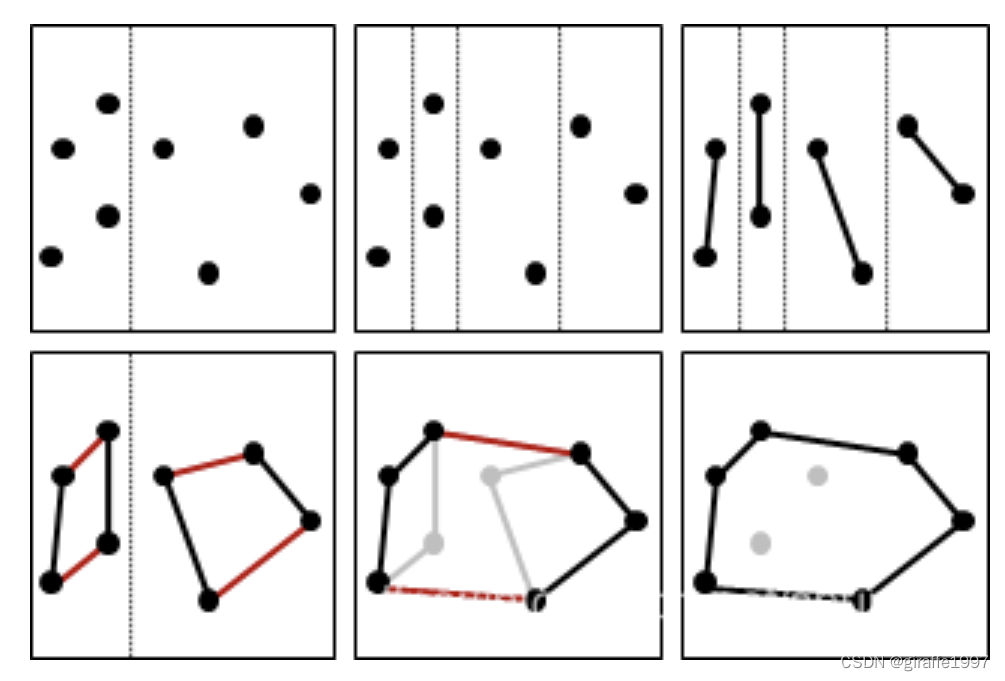
观察两个凸包最上方决定新凸包的两个端点的特征,可以看出他们对于前驱后继都是RR或LL型的,也就是前后相邻的点都落在support line的同侧,其余任两点的连线都只能是LR或RL的。

算法步骤:
step1:找到P1最右边的点和P2最左边的点,上图为r、l两点
step2:从l开始,先固定r不动,看l的前驱后继对于lr组成的线是否是满足RR型(都在右侧),若不满足沿顺时针方向重新寻找l点,如上方的绿色线所示,直到找到满足的点。
step3:然后此时l点固定,看r的前驱后继对于lr组成的线是否是满足LL型,若不满足沿逆时针方向重新寻找符合的r点,如上方的红色线所示,直到找到满足的点。
step4:找可以看到当r点发生移动时,原来的r点不一定还满足RR型了,于是回到step2继续寻找合适的r点
step5:找P1P2最下边的连接点的方法同上,只不过条件变成了满足RR型,l满足LL型
算法复杂度:
算法首先要按照x坐标排序,排序复杂度为O(nlogn)。再看merge过程,无论是左侧子凸包还是右侧子凸包,对于其每个点的操作至多只有以此,也就是每次归并是线性时间。归并共logn次,算法的总体复杂度就是O(nlogn)了。
本文总结来自:计算几何 - 清华大学 - 学堂在线