队列

• 队列是一个有序列表，遵循先入先出的原则；先存入队列的数据，要先取出（出列）。后存入的要后取出（入列）。队列特性简述为First-In-First-Out（FIFO）。
• 队列结构可以来解决在排队情形下的问题，但不要仅局限于排队系统之类的问题。在一些算法中能灵活地运用到队列结构，其关键因素是其特性，FIFO。
• 队列可以用数组或是链表来实现，数组实现更加具有难度，而且比较有代表性。这篇博客我们将介绍如何使用数组实现队列。
  
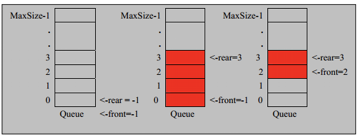
• 图示队列是用数组实现的：

1. 队列容量为MaxSize 。
2. 队列的头部由front记录，front指向头部元素的前一个位置；rear记录队列尾部，rear指向尾部元素。front和rear是数组的下标。（注意，这里非常重要也比较容易混淆，front不是指向头部元素，而rear是指向尾部元素）。
3. 当元素入列时，rear数值加1；元素出列时，front数值加1。
4. 这里显然，该队列有一个缺陷：当有MaxSize数量的元素出列时或rear为MaxSize - 1时，无法再有元素可以入列。那么这就是一个一次性队列，实际应用不是很大。

环形队列

前面我们了解到"一次性"数组的局限性。现在我们来改造一下数组，通过取模运算把数组想象成一个环状的数据顺序存储结构。

• 在改造之前我们来做一些规定，这些规定与前面队列的规定有些区别，需要注意：

1. front指向数组的第一个元素，front初始值为0；rear指向最后元素的后一个位置，初始值为0（因为环状的特点，最后元素的后一个位置为0）。
2. 数组可以储存MaxSize个元素。

• 根据规定我们可以得出几个结论：

1. 当（rear + 1）% MaxSize == front时队列满。
2. 当rear == front队列空。

• 代码实现：

public class CircleQueue {
    private int MaxSize;
    private int [] array;
    private int front;
    private int rear;

    public CircleQueue(int MaxSize){
        this.MaxSize = MaxSize;
        this.array = new int [MaxSize];
        front = 0;
        rear = 0;
    }

    /**
     * Judge if the array is empty.
     * @return, a boolean value
     */
    public boolean isEmpty(){
        return this.front == this.rear;
    }

    /**
     * Judge if the array is full.
     * @return, a boolean value
     */
    public boolean isFull(){
        return (this.rear + 1) % this.MaxSize == this.front;
    }

    /**
     * Make a new element queue in.
     * @param element, new element which queue in to the array.
     */
    public void queueIn(int element){
        if(!isFull()){
            //把当前入列元素放入rear位置
            this.array[this.front] = element;
            return;
        }
        //rear向后移动一个位置，这里的取模运算是防止溢出，也是达到循环效果。
        this.rear = (this.rear + 1) % this.MaxSize;
    }

    /**
     * Make the front element queue out.
     * @return, the front element
     */
    public int queueOut() throws Exception {
        if(isEmpty()){
            throw new Exception("The array is empty!");
        }
        int temp = this.array[this.front];
        this.front = (this.front + 1) % this.MaxSize;
        return temp;
    }

    /**
     * Get a number indicating the elements in array.
     * @return, int value
     */
    public int getElementNumber(){
        //这里的加MaxSize的处理还考虑到了实际数组中rear再front前面
        return (this.rear - this.front + this.MaxSize) % this.MaxSize;
    }

    /**
     * print out all elements in array according to the order.
     */
    public void printArray(){
        //注意，从front开始打印，数组中元素个数控制打印次数，i求余防止溢出。
        for(int i = this.front; i < this.front + getElementNumber();i ++){
            System.out.print(this.array[(i % this.MaxSize)] + " ");
        }
    }

    /**
     * peek the front element.
     * @return, the front element.
     * @throws Exception, throw exception if the array is empty.
     */
    public int peek() throws Exception {
        if(!isEmpty()){
            throw new Exception("The array is empty!");
        }
        return this.array[this.front];
    }
}

• 注意，实现代码的过程中已经把注意事项和关键步骤写明，环形队列的边界条件要仔细想明白。根据其定义和规定来实现代码，并不难。如果想使用该队列储存其他类型元素（更具有实际意义），使用泛型知识改造即可，后面我们会讲到该知识。