注意本篇讲的是如何用一堆离散数据点拟合出高斯模型，而非已知一堆数据点对求解高斯函数。

拟合单高斯模型（正态分布）

若你有一堆离散数据点，想拟合出其高斯分布。实际上只需要求其均值和标准差。

为了好看一点，可以再先出其直方图。一般用plt.hist来画直方图。

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
import math
import matplotlib.mlab as mlab
from scipy.stats import norm


x = np.array(yourlist) 这里填入你的数据list 如果已经是array格式就不用转化了
#n, bins, patches = plt.hist(x, 20, density=1, facecolor='blue', alpha=0.75)  #第二个参数是直方图柱子的数量
mu =np.mean(x) #计算均值 
sigma =np.std(x) 
num_bins = 30 #直方图柱子的数量 
n, bins, patches = plt.hist(x, num_bins,density=1, alpha=0.75) 
#直方图函数，x为x轴的值，normed=1表示为概率密度，即和为一，绿色方块，色深参数0.5.返回n个概率，直方块左边线的x值，及各个方块对象 
y = norm.pdf(bins, mu, sigma)#拟合一条最佳正态分布曲线y 

plt.grid(True)
plt.plot(bins, y, 'r--') #绘制y的曲线 
plt.xlabel('values') #绘制x轴 
plt.ylabel('Probability') #绘制y轴 
plt.title('Histogram : $\mu$=' + str(round(mu,2)) + ' $\sigma=$'+str(round(sigma,2)))  #中文标题 u'xxx' 
#plt.subplots_adjust(left=0.15)#左边距 
plt.show()

结果：

得到单高斯分布后就可以分析概率。

更多画法，参考：《用Python为直方图绘制拟合正态分布曲线的两种方法》

sigma原则

1sigma原则：数值分布在（μ-σ，μ+σ）中的概率为0.6526；

2sigma原则：数值分布在（μ-2σ，μ+2σ）中的概率为0.9544；

3sigma原则：数值分布在（μ-3σ，μ+3σ）中的概率为0.9974；

由于“小概率事件”和假设检验的基本思想 “小概率事件”通常指发生的概率小于5%的事件，认为在一次试验中该事件是几乎不可能发生的。由此可见X落在（μ-3σ，μ+3σ）以外的概率小于千分之三，在实际问题中常认为相应的事件是不会发生的，基本上可以把区间（μ-3σ,μ+3σ）看作是随机变量X实际可能的取值区间，这称之为正态分布的“3σ”原则。

拟合多元高斯分布（高斯混合模型）

用curve_fit！先import：

from scipy.optimize import curve_fit

以三高斯拟合为例，首先先定义高斯拟合函数方程式：

def func3(x,a1,a2,a3,m1,m2,m3,s1,s2,s3):

      return a1*np.exp(-((x-m1)/s1)**2)+a2*np.exp(-((x-m2)/s2)**2)+a3*np.exp(-((x-m3)/s3)**2)

拟合，并对参数进行限制，bounds里面代表参数上下限，参数即为def func3里面x之后的所有参数：

popt, pcov = curve_fit(func3, x, y, bounds=([y0,y0,y0,-5000,-1000,500,1200,1200,1200], [y_max,y_max,y_max,-500,1000,5000,30000,30000,30000]))

这个含义是a1、a2、a3最小值为y0，最大值为y_max,m1、最小值为-5000，最大值为-500，以此类推。

如图所示为拟合出的一个多高斯拟合，这里含有将近10个高斯函数。

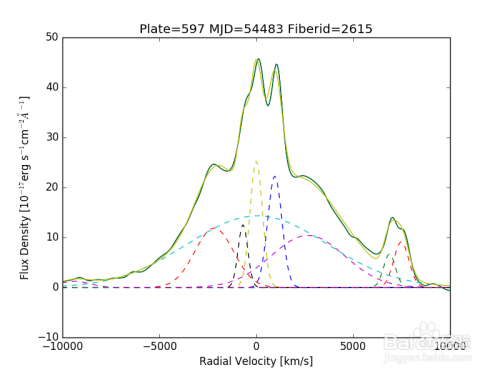
再来一个完整的二元高斯分布的拟合的例子：

import numpy as np
import pylab as plt
#import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
#from scipy import asarray as ar,exp
 
x = ar(range(10))
y = ar([0,1,2,3,4,5,4,3,2,1])
 
 
def gaussian(x,*param):
    return param[0]*np.exp(-np.power(x - param[2], 2.) / (2 * np.power(param[4], 2.)))+\
           param[1]*np.exp(-np.power(x - param[3], 2.) / (2 * np.power(param[5], 2.)))
 
 
popt,pcov = curve_fit(gaussian,x,y,p0=[3,4,3,6,1,1])
print(popt)
print(pcov)
 
plt.plot(x,y,'b+:',label='data')
plt.plot(x,gaussian(x,*popt),'ro:',label='fit')
plt.legend()
plt.show()