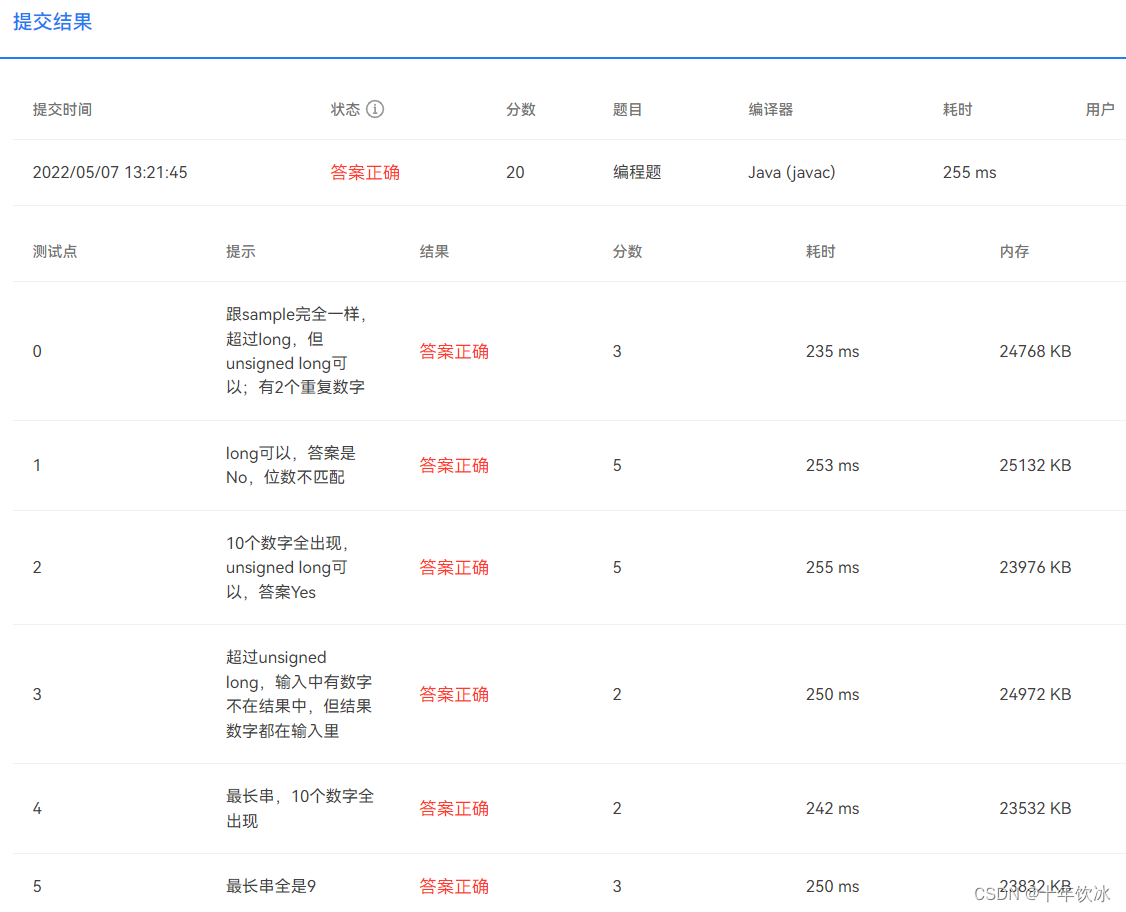
原题:
Notice that the number 123456789 is a 9-digit number consisting exactly the numbers from 1 to 9, with no duplication. Double it we will obtain 246913578, which happens to be another 9-digit number consisting exactly the numbers from 1 to 9, only in a different permutation. Check to see the result if we double it again!
Now you are suppose to check if there are more numbers with this property. That is, double a given number with k digits, you are to tell if the resulting number consists of only a permutation of the digits in the original number.
Input Specification:
Each input contains one test case. Each case contains one positive integer with no more than 20 digits.
Output Specification:
For each test case, first print in a line "Yes" if doubling the input number gives a number that consists of only a permutation of the digits in the original number, or "No" if not. Then in the next line, print the doubled number.
Sample Input:
1234567899
Sample Output:
Yes
2469135798原题题干(稍加润色后):
123456789是一个9位的正整数,这个数字乘2得到246913578,它恰好是另一个由原正整数中的数字组成的9位正整数,而且每个数字出现的次数也和原正整数相同,只是数字的排列顺序不同。现在你应该检查是否有更多的数字具有这个性质,也就是说,将一个给定的含有k个可能相同可能不同的数字的正整数乘2,你要判断结果是否是只包含原始数字的一个排列
输入:
每一种情况包含一个不超过20位的正整数
输出:
如果输入的数字乘2后得到的数字是只包含原始数字的排列,则
首先在第一行中打印“Yes”,如果不是,则打印“No”
然后在下一行中,打印原正整数乘2后得到的正整数
思路:
由于int类型最高可以存储10位左右的数字,而long类型最高大概20位(该题目可能出现21位的),我选择了字符串来接收超级长的正整数。然后将该字符串中的每一位数字都存储到对应字符串数组和整型数组中方便进行逐位操作。字符串数组主要用于向ArrayList添加元素,整型数组主要用于进行乘法运算。得到两个超级长的正整数后,使用List的sort方法先排序,然后转成toString去判断两个集合是否相等,如果相等,那就是满足了两个超级长的正整数只有数字的排列不同,而数字的种类和各自的个数都是相同的。最后分行输出对应结果。
代码:
import java.util.*;
public class Main
{
public static void main(String[] args)
{
//输入超级长的数字组成的字符串,分割每一位存储到字符串数组bit1中,bit2准备用于存储乘法运算结果的每一位
Scanner scanner = new Scanner(System.in);
String number = scanner.next();
String[] bit1 = new String[number.length()];
String[] bit2 = new String[number.length()];
for (int i = 0; i < number.length(); i++)
{
//字符串方法substring有两个形参时截取原字符串指定index区间(左闭右开)内的部分作为新字符串
//字符串方法substring有一个形参时截取原字符串指定index起点的部分作为新字符串
//如果想提取后得到字符类型,用字符串方法charAt(index)
bit1[i] = number.substring(i, i + 1);
}
//把提取出来的单个数字存储到对应的整型数组中
int[] intbit1 = new int[number.length()];
int[] intbit2 = new int[number.length()];
//模拟乘法竖式,设置进位
int addition = 0;
for (int i = 0; i < number.length(); i++)
{
intbit1[i] = Integer.parseInt(bit1[i]);
}
for(int i = number.length() - 1; i >= 0; i--)
{
if(i >= 1)
{
//对于非最高位,都先进行当前数位的运算然后再得到下次循环中更高数位的进位
intbit2[i] = intbit1[i] * 2 % 10 + addition;
addition = intbit1[i] * 2 / 10;
}
else
{
//对于最高位,正常运算,没有非最高位需要保证一位的要求
intbit2[i] = intbit1[i] * 2 + addition;
}
}
//将进行乘法运算后得到的每一位数存储到之前准备的字符串数组中,方便存储到集合中
for (int i = 0; i < intbit2.length; i++)
{
bit2[i] = String.valueOf(intbit2[i]);
}
//List.of里面的String数组不能有null
//这里逐个将字符串数组中的元素add进ArrayList中
//原正整数对应的ArrayList
List<String> sortedNumber1 = new ArrayList();
for (int i = 0; i < bit1.length; i++)
{
sortedNumber1.add(bit1[i]);
}
//乘法运算后新得到的ArrayList
List<String> sortedNumber2= new ArrayList();
for (int i = 0; i < bit2.length; i++)
{
sortedNumber2.add(bit2[i]);
}
//更方便的存储方法是:
//List<String> sortedNumber1 = new ArrayList<>(List.of(bit1));
//List<String> sortedNumber2 = new ArrayList<>(List.of(bit1));
//但是这个方法在PTA中总是编译错误,所以我选择了更简单的方法
//使用List的sort方法先排序,然后转成toString去判断两个集合是否相等
sortedNumber1.sort(Comparator.comparing(String::hashCode));
sortedNumber2.sort(Comparator.comparing(String::hashCode));
//输出第一行
if(sortedNumber1.toString().equals(sortedNumber2.toString()))
{
System.out.println("Yes");
}
else
{
System.out.println("No");
}
//输出第二行
for (int i:intbit2)
{
System.out.print(i);
}
}
}