不撞南墙不回头-深度优先搜索
广度优先搜索BFS是每次将当前状态能够一步拓展出的所有状态,全部拓展出来依次存入队列。而深度优先搜索是将当前状态按照一定的规则顺序,先拓展一步得到一个新状态,再对这个这个新状态递归拓展下去。如果无法拓展,则退回一步到上一步的状态,再按照原先设定的规则顺序重新寻找一个状态拓展。如此搜索,直到找到目标状态,或者遍历完所有的状态。
深度优先搜索
深度优先搜索(Depth First Search,DFS),简称 深搜 ,其状态“退后一步”的顺序符合“后进先出”的特点,所以采用“栈”存储状态。深搜的空间复杂度较小,因为它只存储了初始状态到当前状态的一条搜索路径。但是,深搜找到的第一个解不一定是最优解,要找最优解必须搜索整棵“搜索树”。所以,深搜适用于要求所有解方案的题目。
相信通过上面的描述,同学们还是对深度优先搜索一头雾水。下面我们结合一个例子,和大家一起探索下什么是深度优先搜索。深度优先搜索可以这样想,一个人迷路了,遇到很多分叉路口,他只有一个人,并且想走出去,所以他只能一个个路线的去尝试, 一条道路走到黑,发现到头了,然后再退回去走刚才这条路的其他分叉路口,最后发现这条路的所有分叉路口走完了,选择另外一条路继续以上操作,直到所有的路都走过了。
而广度优先并不是这样,一个人迷路了,但是他有特异技能(就好比火影里面鸣人的影分身一样), 他遇到分叉路口,不是选一个走,而是分身多个人每个路口都去试试 ,比如有A、B、C三个分叉路口,A路走一步,紧接着B路也走一步,然后C路也赶紧走一步,步伐整齐统一,直到所有的路走过了。
深度优先搜索的步骤
深度优先搜索的步骤分为 1.递归下去 2.回溯上来。顾名思义,深度优先,则是以深度为准则,先一条路走到底,直到达到目标,这里称之为递归下去。否则既没有达到目标又无路可走了,那么则退回到上一步的状态,走其他路,这便是回溯上来。下面结合具体例子来理解。如图所示,在一个迷宫中,黑色块代表玩家所在位置,红色块代表终点,问是否有一条到终点的路径。
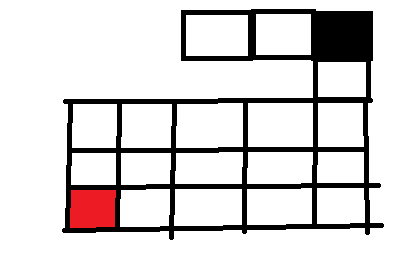
我们用深度优先搜索的方法去解这道题,由图可知,我们可以走上下左右四个方向,我们规定按照 左下右上 的方向顺序走(逆时针方向),即如果左边可以走,我们先走左边。然后递归下去,没达到终点,我们再回溯上来,等又回溯到这个位置时,左边已经走过了,那么我们就走下边,按照这样的顺序与方向走。并且我们把走过的路标记一下代表走过,不能再走。所以我们从黑色起点首先向左走,然后发现还可以向左走,最后我们到达图示位置。
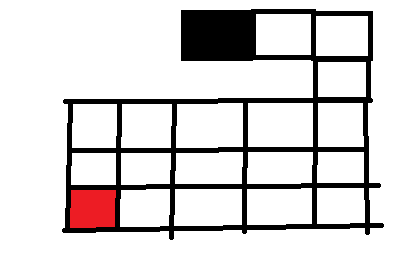
已经连续向左走到左上角的位置了,这时发现左边不能走了,这时我们就考虑往下走,发现也不能走,同理,上边也不能走, 右边已经走过了也不能走,这时候无路可走了 ,代表这条路是死路不能帮我们解决问题, 所以现在要回溯上去,回溯到上一个位置。
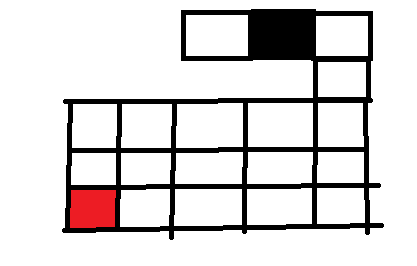
在这个位置我们由上可知走左边是死路不行,上下是墙壁不能走,而右边又是走过的路,已经被标记过了,不能走。所以只能再度回溯到上一个位置寻找别的出路。

最终我们回溯到最初的位置,同理,左边证明是死路不必走了,上和右是墙壁, 所以我们走下边 。然后递归下去
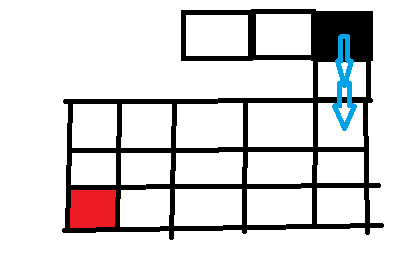
到了这个格子,因为按照左下右上的顺序,我们走左边,递归下去
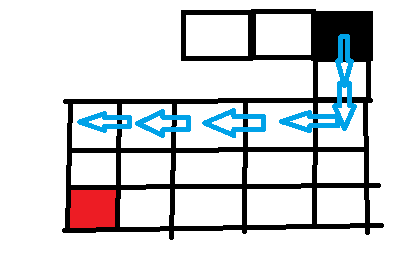
一直递归下去到最左边的格子,然后左边行不通,走下边,一直往下走,正好可以找到目标位置。
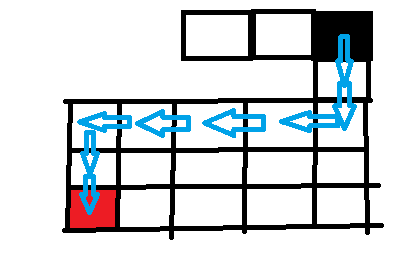
广度优先搜索较之深度优先搜索之不同在于,深度优先搜索旨在不管有多少条岔路, 先一条路走到底,不成功就返回上一个路口然后就选择下一条岔路 ,而广度优先搜索旨在面临一个路口时,把所有的岔路口都记下来,然后选择其中一个进入,然后将它的分路情况记录下来,然后再返回来进入另外一个岔路,并重复这样的操作,用图形来表示则是这样的,例子同上。
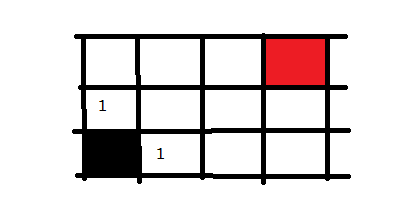
从黑色起点出发,记录所有的岔路口,并标记为走一步可以到达的。然后选择其中一个方向走进去,我们走黑点方块上面的那个,然后将这个路口可走的方向记录下来并标记为2,意味走两步可以到达的地方。
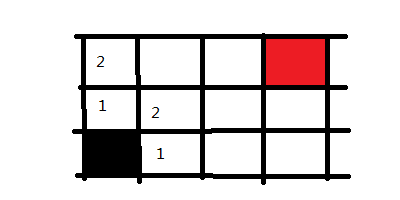
接下来,我们回到黑色方块右手边的1方块上,并将它能走的方向也记录下来,同样标记为2,因为也是走两步便可到达的地方
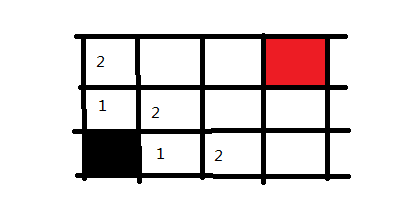
这样走一步以及走两步可以到达的地方都搜索完毕了,下面同理,我们可以迅速把三步的格子给标记出来
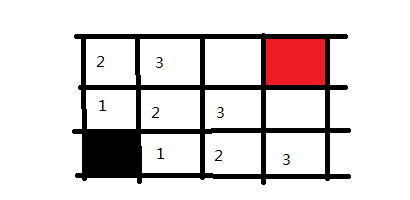
再之后是四步,五步。
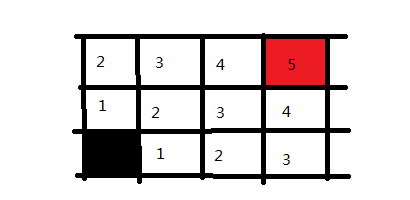
我们便成功寻找到了路径,并且把所有可行的路径都求出来了。
广度优先搜索和深度优先搜索的比较
在广度优先搜索中,可以看出是逐步求解的,反复的进入与退出,将当前的所有可行解都记录下来,然后逐个去查看。 在DFS中我们说关键点是递归以及回溯,在BFS中,关键点则是状态的选取和标记。
对于这两个搜索方法,其实我们是可以轻松的看出来,他们有许多差异与许多相同点的。
1.数据结构上的运用
DFS用递归的形式,用到了 栈 结构,先进后出。
BFS选取状态用 队列 的形式,先进先出。
2.复杂度
DFS的复杂度与BFS的复杂度大体一致,不同之处在于遍历的方式与对于问题的解决出发点不同,DFS适合目标明确,而BFS适合大范围的寻找。
3.思想
思想上来说这两种方法都是穷竭列举所有的情况。
我相信很多同学看完上面的内容对深度优先搜索还不是很熟悉。下面我们通过几个例子带同学们更深入的了解什么是深度优先搜索。
案例1:扑克牌游戏
假如有编号为1、2、3的3张扑克牌和编号为1、2、3的3个盒子。现在需要将这3张扑克牌分别放到3个盒子里面,并且每个盒子有且只能放一张扑克牌。那么一共有多少种不同的放法呢?
聪明的拓拓觉得这个题目很简答,于是他决定试一试。拓拓手拿 3张扑克牌,首先走到了1号盒子面前。此时拓拓心里想∶我是先放1号扑克牌,还是先放2号扑克牌,还是先放3号扑克牌呢?很显然这三种情况都需要去尝试,拓拓说那我们约定一个顺序吧∶每次到一个盒子面前时,都先放1号,再放2号,最后放3号扑克牌。说完拓拓走到了1号盒子前,将 1号扑克牌放到第1个盒子中。
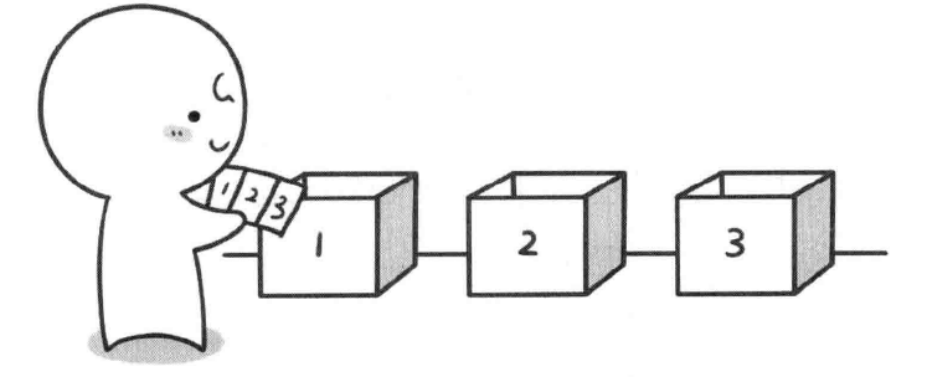
放好之后拓拓往后走一步,来到了2号盒子面前。本来按照之前约定的规则,每到一个新的盒子面前,要按照1号、2号、3号扑克牌的顺序来放。但是现在拓拓手中只剩下2号和3号扑克牌了,于是拓拓将2号扑克牌放入了2号盒子中。放好之后拓拓再往后走一步,来到了3号盒子面前。
现在拓拓已经来到了3号盒子面前,按照之前约定的顺序,还是应该按照1号、2号、3号扑克牌的顺序来放,但是拓拓手中只有3号扑克牌了,于是只能往 3号盒子里面放3号扑克牌。放好后,拓拓再往后走一步,来到了4号盒子面前。咦!没有第4个盒子,其实我们并不需要第 4个盒子,因为手中的扑克牌已经放完了。我们发现当拓拓走到第4个盒子的时候,已经完成了一种排列,这个排列就是前面3个盒子中的扑克牌号码,即"123"。
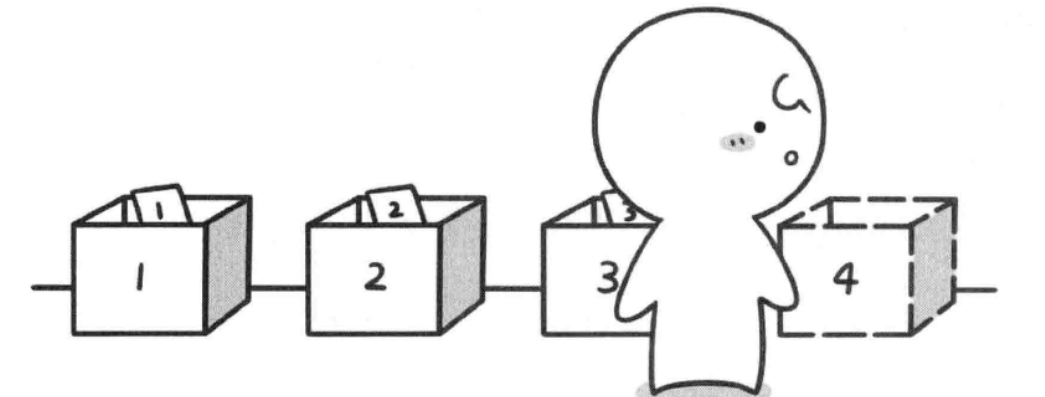
是不是游戏到此就结束了呢?肯定没有!产生了一种排列之后拓拓需要立即返回。现在拓拓需要退一步重新回到 3 号盒子面前。好!现在拓拓已经回到了3号盒子面前,需要取回之前放在3号盒子中的扑克牌,再去尝试看看还能否放别的扑克牌,从而产生一个新的排列。
于是拓拓取回了3号扑克牌。当拓拓再想往3号盒子放别的扑克牌的时候,却发现手中仍然只有3号扑克牌,没有别的选择。于是拓拓不得不再往回退一步,回到2 号盒子面前。拓拓回到2号盒子后,收回了2号扑克牌。现在拓拓手里面有两张扑克牌了,分别是2号和3号扑克牌。按照之前约定的顺序,现在需要往2号盒子中放3号扑克牌(上一次放的是2号扑克牌)。放好之后拓拓又向后走一步,再次来到了3号盒子面前。拓拓再次来到3号盒子后,将手中仅剩的2号扑克牌放入了3号盒子。又来到4号盒子面前。当然了,这里并没有4号盒子。此时又产生了一个新的排列“132”。
接下来按照刚才的步骤去模拟,便会依次生成所有排列∶"213""231""312"和"321"。
说了半天,这么复杂的过程如何用程序实现呢?我们现在来解决最基本的问题∶如何往小盒子中放扑克牌。每一个小盒子都可能放1号、2号或者3号扑克牌,这需要一一去尝试,这里一个 for循环就可以解决。
for(i=1;i<=n;i++)
{
a[step]=i; //将第i号扑克牌放入第step个盒子中
}
Copy
这里数组 a是用来表示小盒子的,变量 step 表示当前正处在第 step 个小盒子面前。 a[step]=i; 就是将第i号扑克牌放入到第step个盒子中。这里有一个问题那就是,如果一张扑克牌已经放到别的小盒子中了,那么此时就不能再放入同样的扑克牌到当前小盒子中,因为此时手中已经没有这张扑克牌了。因此还需要一个数组 book来标记哪些牌已经使用了。
for(i=1;i<=n;i++)
{
if(book[i]==0)
{
a[step]=i; //将第i号扑克牌放入第step个盒子中
book[i]=1; //将book[i]设为1,表示滴i号牌已经不在手中了
}
}
Copy
OK,现在已经处理完第 step个小盒子了,接下来需要往下走一步,继续处理第 step+1个小盒子。那么如何处理第 step+1个小盒子呢?处理方法其实和我们刚刚处理第 step个小盒子的方法是相同的。因此就很容易想到(如果这个词伤害了您,我表示深深的歉意^^)把刚才的处理第 step 个小盒子的代码封装为一个函数,我们为这个函数起个名字,就叫做dfs 吧,如下。
void dfs(int step) //step表示现在站在第几个盒子面前
{
for(i=1;i<=n;i++)
{
//判断扑克牌i是否还在手上
if(book[i]==0) //将book[i]等于0表示扑克牌仍然在手上
{
a[step]=i; //将第i号扑克牌放入第step个盒子中
book[i]=1; //将book[i]设为1,表示滴i号牌已经不在手中了
}
}
}
Copy
把这个过程写成函数后,刚才的问题就好办了。在处理完第 step个小盒子之后,紧接着处理第 step+1个小盒子,处理第step+1和小盒子的方法就是 dfs(step+1),请注意下面代码中第11行语句。
void dfs(int step) //step表示现在站在第几个盒子面前
{
for(i=1;i<=n;i++)
{
//判断扑克牌i是否还在手上
if(book[i]==0) //将book[i]等于0表示扑克牌仍然在手上
{
a[step]=i; //将第i号扑克牌放入第step个盒子中
book[i]=1; //将book[i]设为1,表示滴i号牌已经不在手中了
dfs(step+1); //这里通过函数的递归用来实现
book[i]=0; //这是非常重要的一步,一定要将刚才尝试的扑克牌收回,才能进行下一次尝试
}
}
}
Copy
上面代码中的book[i]=0;这条语句非常重要,这句话的作用是将小盒子中的扑克牌收回,因为在一次摆放尝试结束返回的时候,如果不把刚才放入小盒子中的扑克牌收回,那将无法再进行下一次摆放。还剩下一个问题,就是什么时候该输出一个满足要求的序列呢。其实当我们处理到第 n+1个小盒子的时候(即 step等于n+1),那么说明前n个盒子都已经放好扑克牌了,这里就将 1-n个小盒子中的扑克牌编号打印出来就可以了,如下。注意!打印完毕一定要立即 return,不然这个程序就会永无止境地运行下去了,想一想为什么吧。
完整的代码如下所示:
#include<bits/stdc++.h>
using namespace std;
int a[10],book[10],n;
void dfs(int step) //step表示现在站在第几个盒子面前
{
int i;
if(step==n+1) //如果站在第n+1个盒子面前,则表示前n个盒子已经放在扑克牌
{
//输出一种排列(1-n号盒子中的扑克牌编号)
for(i=1;i<=n;i++)
{
cout<<a[i]<<" ";
}
cout<<endl;
return; //返回之前一步(最近一次调用dfs函数的地方)
}
//此时站在第step个盒子前,应该放哪张牌呢?
//按照1、2、3...n的顺序一一尝试
for(i=1;i<=n;i++)
{
//判断扑克牌i是否还在手上
if(book[i]==0) //将book[i]等于0表示扑克牌仍然在手上
{
//开始尝试使用扑克牌i
a[step]=i; //将第i号扑克牌放入第step个盒子中
book[i]=1; //将book[i]设为1,表示滴i号牌已经不在手中了
//第step个盒子已经放好扑克牌,接下来需要走到下一个盒子面前
dfs(step+1); //这里通过函数的递归用来实现
book[i]=0; //这是非常重要的一步,一定要将刚才尝试的扑克牌收回,才能进行下一次尝试
}
}
}
int main()
{
cin>>n;
dfs(1); //首先站在1号盒子前面
return 0;
}
Copy
这个简单的例子,核心代码不超过20行,却饱含深度优先搜索(DepthFirst Search,DFS)的基本模型。理解深度优先搜索的关键在于解决当下该如何做。至于下一步如何做则与当下该如何做是一样的。比如我们这里写的dfs(step)函数的主要功能就是解决当你在第 step个盒子的时候你该怎么办。通常的方法就是把每一种可能都去尝试一遍(一般使用 for 循环来遍历)。当前这一步解决后便进入下一步dfs(step+1)。下一步的解决方法和当前这步的解决方法是完全一样的。下面的代码就是深度优先搜索的基本模型。
void dfs(int step)
{
判断边界
尝试每一种可能 for(i=1;i<=n;i++)
{
继续下一步 dfs(step+1);
}
返回
}
Copy
案例2:解救小拓
有一天,小拓一个人去玩迷宫。但是方向感很不好的小拓很快就迷路了。小哼得知后便立即去解救无助的小拓。小哼当然是有备而来,已经弄清楚了迷宫的地图,现在小哼要以最快的速度去解救小拓。问题就此开始了……
迷宫由n行m列的单元格组成(n和m都小于等于50),每个单元格要么是空地,要么是障碍物。你的任务是帮助小哼找到一条从迷宫的起点通往小拓所在位置的最短路径。注意障碍物是不能走的,当然小哼也不能走到迷宫之外。
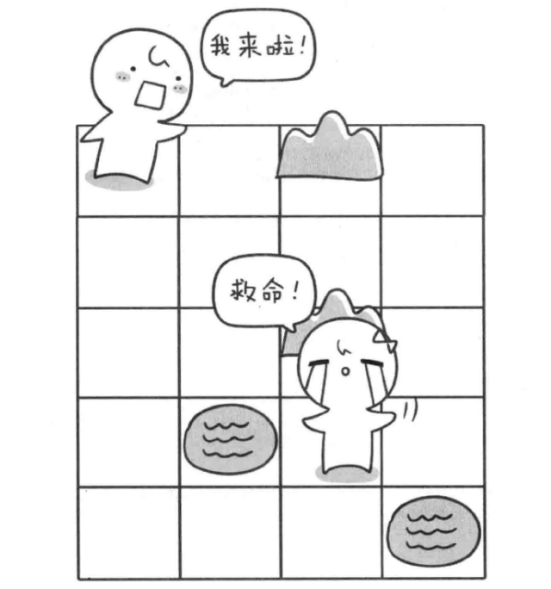
首先我们可以用一个二维数组来存储这个迷宫,刚开始的时候,小哼处于迷宫的入口处(1,1),小拓在(p,q)。其实,就是找从(1,1)到(p,q)的最短路径。如果你是小哼,你该怎么办呢?小哼最开始在(1,1),他只能往右走或者往下走,但是小哼是应该往右走呢还是往下走呢。此时要是能有两个小哼就好了,一个向右走,另外一个向下走。但是现在只有一个小哼,所以只能一个一个地去尝试。我们可以先让小哼往右边走,直到走不通的时候再回到这里,再去尝试另外一个方向。我们这里规定一个顺序,按照顺时针的方向来尝试(即按照右、下、左、上的顺序去尝试)。
我们先来看看小哼一步之内可以达到的点有哪些?只有(1,2)和(2,1)。根据刚才的策略,我们先往右边走,小哼来到了(1,2)这个点。来到(1,2)之后小哼又能到达哪些新的点呢?只有(2,2)这个点。因为(1,3)是障碍物无法达到,(1,1)是刚才来的路径中已经走过的点,也不能走,所以只能到(2,2)这个点。但是小拓并不在(2,2)这个点上,所以小哼还得继续往下走,直至无路可走或者找到小拓为止。请注意!此处并不是一找到小拓就结束了。因为刚才只尝试了一条路,而这条路并不一定是最短的。刚才很多地方在选择方向的时候都有多种选择,因此我们需要返回到这些地方继续尝试往别的方向走,直到把所有可能都尝试一遍,最后输出最短的一条路径。例如下图就是一种可行的搜索路径。
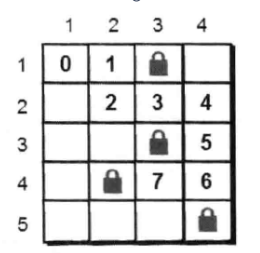
现在我们尝试用深度优先搜索来实现这个方法。先来看 dfs()函数如何写。dfs()函数的功能是解决当前应该怎么办。而小哼处在某个点的时候需要处理的是∶先检查小哼是否已经到达小拓的位置,如果没有到达则找出下一步可以走的地方。为了解决这个问题,此处 dfs()函数只需要3个参数,分别是当前这个点的x坐标、y坐标以及当前已经走过的步数 step。 dfs()函数定义如下。
void dfs(int x,int y,int step)
{
return ;
}
Copy
是否已经到达小拓的位置这一点很好实现,只需要判断当前的坐标和小拓的坐标是否相等就可以了,如果相等则表明已经到达小拓的位置,如下。
void dfs(int x,int y,int step)
{
//判断是否到达小拓的位置
if(x==p && y==q)
{
//更新最小值
if(step<min)
{
min=step;
}
return ; //请注意这里返回很重要
}
return ;
}
Copy
如果没有到达小拓的位置,则找出下一步可以走的地方。因为有四个方向可以走,根据我们之前的约定,按照顺时针的方向来尝试(即按照右、下、左、上的顺序尝试)。这里为了编程方便,我定义了一个方向数组 next,如下。
int next[4][2]={{0,1}, //向右走
{1,0}, //向下走
{0,-1}, //向左走
{-1,0}}; //向上走
Copy
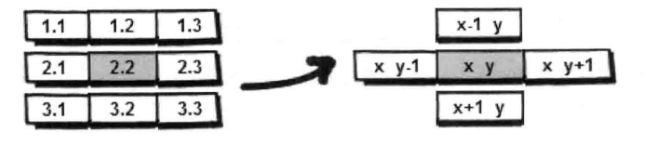
通过这个方向数组,使用循环就很容易获得下一步的坐标。这里将下一步的横坐标用 tx存储,纵坐标用 ty 存储。
for(k=0;k<=3;k++)
{
//计算的下一个点坐标
tx=x+next[k][0];
ty=y+next[k][1];
}
Copy
接下来我们就要对下一个点(x,ty)进行一些判断。包括是否越界,是否为障碍物,以及这个点是否已经在路径中(即避免重复访问一个点)。需要用book[tx][ty]来记录格子(tx,ty)是否已经在路径中。如果这个点符合所有的要求,就对这个点进行下一步的扩展,即 dfs(tx,ty,step+1),注意这里是 step+1,因为一旦你从这个点开始继续往下尝试,就意味着你的步数已经增加了1。
完整的代码实现如下:
#include<bits/stdc++.h>
using namespace std;
int n,m,p,q,mmin=999999;
int a[51][51],book[51][51];
void dfs(int x,int y,int step)
{
int next[4][2]={{0,1}, //向右走
{1,0}, //向下走
{0,-1}, //向左走
{-1,0}}; //向上走
int tx,ty,k;
//判断是否到达小拓的位置
if(x==p && y==q)
{
//更新最小值
if(step<mmin)
{
mmin=step;
}
return ; //请注意这里返回很重要
}
//枚举四种走法
for(k=0;k<=3;k++)
{
//计算的下一个点坐标
tx=x+next[k][0];
ty=y+next[k][1];
//判断是否越界
if(tx<1||tx>n||ty<1||ty>m)
continue;
//判断该点是否为障碍物或者已经在路径中
if(a[tx][ty]==0&&book[tx][ty]==0)
{
book[tx][ty]=1; //标记这个点已经走过
dfs(tx,ty,step+1); //开始尝试下一个点
book[tx][ty]=0; //尝试结束后,取消这个点的标记
}
}
return ;
}
int main()
{
int i,j,startx,starty;
cin>>n>>m;
for(i=1;i<=n;i++)
{
for(j=1;j<=m;j++)
{
cin>>a[i][j]; //读入迷宫
}
}
cin>>startx>>starty>>p>>q; //读入开始和结束坐标
//从起点开始搜索
book[startx][starty]=1; //标记该点已经在路径中,反正后面重复走
//第一个参数是起点的x的坐标,第二个参数是起点的y坐标,第三个参数是初始步数为0
dfs(startx,starty,0);
//输出最短步数
cout<<mmin;
return 0;
}
Copy
可以输入以下数据进行验证。第一行有两个数n和m。n表示迷宫的行,m表示迷宫的列。接下来的n行m列为迷宫,0表示空地,1表示障碍物。最后一行 4个数,前两个数为迷宫入口的x和y坐标。后两个为小拓的x和y坐标。运行结果是7。
5 4
0 0 1 0
0 0 0 0
0 0 1 0
0 1 0 0
0 0 0 1
1 1 4 3
Copy
经典例题讲解:
例题1:全排列问题(主题库2696)
输出自然数 1\sim n1∼n 所有不重复的排列,即 nn 的全排列,要求所产生的任一数字序列中不允许出现重复数字。
输入格式:一行,一个整数 nn。
输出格式:输出由 1\sim n1∼n 组成的所有不重复的数字序列。每行一个序列,行内数字之间用空格隔开。
样例输入:
3
Copy
样例输出:
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
Copy
数据范围:
对于 100% 的测试数据满足:1≤n≤91≤n≤9。
解题思路:看到这个题目,如果你还有一丝丝的疑惑就表示你对上面的第一个案例还没有弄明白,所谓的全排列的问题跟案例一扑克牌游戏其实是完全一样的题目。如果你直接把案例一的代码递交上去,会发现是可以直接ac的。
完整的代码如下:
#include<bits/stdc++.h>
using namespace std;
int a[10],book[10],n;
void dfs(int step) //step表示现在站在第几个盒子面前
{
int i;
if(step==n+1) //如果站在第n+1个盒子面前,则表示前n个盒子已经放在扑克牌
{
//输出一种排列(1-n号盒子中的扑克牌编号)
for(i=1;i<=n;i++)
{
cout<<a[i]<<" ";
}
cout<<endl;
return; //返回之前一步(最近一次调用dfs函数的地方)
}
//此时站在第step个盒子前,应该放哪张牌呢?
//按照1、2、3...n的顺序一一尝试
for(i=1;i<=n;i++)
{
//判断扑克牌i是否还在手上
if(book[i]==0) //将book[i]等于0表示扑克牌仍然在手上
{
//开始尝试使用扑克牌i
a[step]=i; //将第i号扑克牌放入第step个盒子中
book[i]=1; //将book[i]设为1,表示滴i号牌已经不在手中了
//第step个盒子已经放好扑克牌,接下来需要走到下一个盒子面前
dfs(step+1); //这里通过函数的递归用来实现
book[i]=0; //这是非常重要的一步,一定要将刚才尝试的扑克牌收回,才能进行下一次尝试
}
}
}
int main()
{
cin>>n;
dfs(1); //首先站在1号盒子前面
return 0;
}
Copy
例题2:素数环(主题库1348)
如图所示为一个由 n个圆圈构成的圆环。将自然数 1,2,...,n放入圆圈内,并且要求任意两个相邻的圆圈内的数字之和为素数。请问给你圆圈数,你能给出放置自然数的所有正确方案吗?

注意:圆圈中的数字一定是从1开始的,并且连续不重复。
输入格式:n(1<=n<=17)。
输出格式:把1放在第一位置,按照字典顺序不重复的输出所有解(顺时针,逆时针算不同的两种),相邻两数之间严格用一个整数隔开,每一行的末尾不能有多余的空格。 如果没有答案请输出"no answer"。
样例输入:
8
Copy
样例输出:
1 2 3 8 5 6 7 4
1 2 5 8 3 4 7 6
1 4 7 6 5 8 3 2
1 6 7 4 3 8 5 2
Copy
解题思路:仔细分析本道题,其实会发现跟全排列的题目有相似的地方,同样是n个不同的数字,只是本道题目里面的数字需要满足任意两个相邻的圆圈内的数字之和为素数。根据题意,把1放在第一位置,因此第一位一定是1,所以我们可以从第2个数开始搜索,同时把1标记为用过use[1]=1;。接下来我们开始写dfs()函数,用cur表示当前搜索到第几个数,如果当前这个数大于n,则搜索结束,搜索结束就可以输出一种可能性,这里需要特别注意的是还需要判断一下最后一个数跟第一个数字1的和是不是也是素数,这一点特别容易忽视。接下来开始写循环语句,从第2个数循环到第n个数,限制条件很简单,包括两个,一个是这个点没有用过即use[i]==0;另一个是这个点跟上一个点之和为素数,即prime(i+a[cur-1])==1(你也可以用素数筛来判断素数)。如果i满足限制条件就可以把i存在a[cur]里面,同时把i标记为1,即use[i]=1;这个数搞定了,紧接着,我们就可以开始搜索下一个数了,下一个数完全跟上一个数的搜索方法一样,因此可以直接调用dfs()函数,即dfs(cur+1);接下来就是最重要的一步,将i再标记成0。
完整代码如下所示:
#include<bits/stdc++.h>
using namespace std;
int a[20],use[20];
int n, ans=0;
bool prime(int x){ //素数判断
for(int i=2;i<=sqrt(x);i++)
{
if(x%i==0) return 0;
}
return 1;
}
void print(){ //输出
for(int i=1;i<=n;i++)
{
cout<<a[i]<<" ";
}
cout<<endl;
}
void dfs(int cur){ //cur表示当前是第几个数
if(cur>n){ //如果大于n,即n个数都输入环中,结束
if(prime(a[1]+a[n])==1){ //结束的时候,还需要判断第n个数跟第一个数之和是不是素数
ans++;
print(); //如果成立,则输出这种排法
return;
}
}
for(int i=2;i<=n;i++) //从第2个数开始搜索
{
if(use[i]==0&&prime(i+a[cur-1])==1) //这个点没有搜过并且这个点跟上个点加起来是素数
{
a[cur]=i; //i保存在当前位置
use[i]=1; //这个数字搜过了,标记为1
dfs(cur+1); //开始搜下一个数
use[i]=0; //回溯,这个点又标记为0
}
}
}
int main()
{
cin>>n;
a[1]=1;
use[1]=1; //1一开始就被搜了,容易忽视
dfs(2); //从2开始搜索
if(ans==0) cout<<"no answer";
return 0;
}
Copy
例题3:马走日(主题库2678)
马在中国象棋以日字形规则移动。
请编写一段程序,给定n×m大小的棋盘,以及马的初始位置(x,y),要求不能重复经过棋盘上的同一个点,计算马可以有多少途径遍历棋盘上的所有点。
输入格式:第一行为整数T(T < 10),表示测试数据组数。
每一组测试数据包含一行,为四个整数,分别为棋盘的大小以及初始位置坐标n,m,x,y。(0≤x≤n-1,0≤y≤m-1, m < 10, n < 10)。
输出格式:每组测试数据包含一行,为一个整数,表示马能遍历棋盘的途径总数,0为无法遍历一次。
样例输入:
1
5 4 0 0
Copy
样例输出:
32
Copy
解题思路:类似于马走日这种题目,我们很明显想到用搜索的方法。题目里面问的是马能遍历棋盘的途径总数,所谓遍历棋盘就是马移动的步数是不是正好等于棋盘的大小。即搜索的结束条件为num==n*m。由于是多组测试数组,因此千万别忘记了清理,这里使用了memset(f,0,sizeof(f));进行清零。首先从起始点开始搜索,因此起始点标记为1。马移动有八个方向即dir[8][2]={{2,1},{2,-1},{1,2},{1,-2},{-1,2},{-1,-2},{-2,1},{-2,-1}}。对于每个点还需要判断是否越界,这里用一个check函数检测是否超过棋盘的界限。dfs()函数里面包含3个参数,分别是起始点的位置和点的数目。如果点数正好等于棋盘的格数则方法的数目加1,如果不是从八个方向开始搜索,搜索的限制条件同样为两个是否越界,以及这个点未走过。如果满足条件,则该点标记为1,开始搜索下一个点,同时清空。
完整的代码如下所示:
#include<bits/stdc++.h>
using namespace std;
const int dir[8][2]={{2,1},{2,-1},{1,2},{1,-2},{-1,2},{-1,-2},{-2,1},{-2,-1}}; //马可以走的八个方向
int t,n,m,x,y,ans=0;
bool f[15][15]; //标记每个点是否走过
bool check(int x,int y){ //检测是否超过棋盘的界限
if(x>=0&&x<n&&y>=0&&y<m){
return 1;
}
else
return 0;
}
void dfs(int x,int y,int num){ //xy表示马所在的位置,num表示点的数目
if(num==n*m){ //当数目等于棋盘数表示成立
ans++;
return;
}
else{
for(int i=0;i<8;i++) //不够的话开始搜索
{
int dx=x+dir[i][0]; //横坐标的值为二维数组dir的00,10,20,30...
int dy=y+dir[i][1]; //纵坐标的值为二维数组dir的00,01,02,03...
if(check(dx,dy)==1&&f[dx][dy]==0){ //如果这个点没有越界并且这个点还没有走过
f[dx][dy]=1; //这个点走过了,标记
dfs(dx,dy,num+1); //开始搜索下一个点
f[dx][dy]=0; //清空标记
}
}
}
}
int main()
{
cin>>t;
while(t--)
{
ans=0;
memset(f,0,sizeof(f)); //多组输入的清零
cin>>n>>m>>x>>y;
f[x][y]=1; //开始位置肯定为1
dfs(x,y,1); //从第一个点开始搜索
cout<<ans<<endl;
}
return 0;
}
Copy