LeetCode 112 路径总和
给定一个二叉树和一个目标和,判断该树中是否存在根节点到叶子节点的路径,这条路径上所有节点值相加等于目标和。
说明: 叶子节点是指没有子节点的节点。
示例:
给定如下二叉树,以及目标和 sum = 22,
5
/ \
4 8
/ / \
11 13 4
/ \ \
7 2 1
返回 true, 因为存在目标和为 22 的根节点到叶子节点的路径 5->4->11->2。
class Solution:
def hasPathSum(self, root: TreeNode, sum: int) -> bool:
if not root:
return False
if not root.left and not root.right:
return sum == root.val
return self.hasPathSum(root.left, sum - root.val) or self.hasPathSum(root.right, sum - root.val)
LeetCode 求和路径(剑指oofer 04.12)
给定一棵二叉树,其中每个节点都含有一个整数数值(该值或正或负)。设计一个算法,打印节点数值总和等于某个给定值的所有路径的数量。注意,路径不一定非得从二叉树的根节点或叶节点开始或结束,但是其方向必须向下(只能从父节点指向子节点方向)。
示例:
给定如下二叉树,以及目标和 sum = 22,
5
/ \
4 8
/ / \
11 13 4
/ \ / \
7 2 5 1
返回:
3
解释:和为 22 的路径有:[5,4,11,2], [5,8,4,5], [4,11,7]
先计算包含根节点的情况,在递归求解不包含根节点的左右子树,统计相加即可。
class Solution:
def pathSum(self, root: TreeNode, sum: int) -> int:
if not root:
return 0
# 递归求解不包含根节点的左右子树,并且相加
return self.path(root, sum) + self.pathSum(root.left, sum) + self.pathSum(root.right, sum)
# 计算包含根节点的情况
def path(self, root, s):
if not root:
return 0
res = 0
if root.val == s:
res += 1
res += self.path(root.left, s - root.val)
res += self.path(root.right, s - root.val)
return res
LeetCode 124. 二叉树中的最大路径和
给定一个非空二叉树,返回其最大路径和。
本题中,路径被定义为一条从树中任意节点出发,达到任意节点的序列。该路径至少包含一个节点,且不一定经过根节点。
示例 1:
输入: [1,2,3]
1
/ \
2 3
输出: 6
示例 2:
输入: [-10,9,20,null,null,15,7]
-10
/ \
9 20
/ \
15 7
输出: 42
class Solution:
def maxPathSum(self, root: TreeNode) -> int:
if not root:
return 0
self.maxval = -float('inf')
self.dfs(root)
return self.maxval
def dfs(self, root):
if not root:
return 0
left = self.dfs(root.left)
right = self.dfs(root.right)
maxval = max(root.val, root.val + left, root.val + right, root.val + left + right)
self.maxval = max(maxval, self.maxval)
return max(root.val, root.val + left, root.val + right)
剑指 Offer 34. 二叉树中和为某一值的路径
输入一棵二叉树和一个整数,打印出二叉树中节点值的和为输入整数的所有路径。从树的根节点开始往下一直到叶节点所经过的节点形成一条路径。
示例:
给定如下二叉树,以及目标和 sum = 22,
5
/ \
4 8
/ / \
11 13 4
/ \ / \
7 2 5 1
返回:
[
[5,4,11,2],
[5,8,4,5]
]
class Solution:
def pathSum(self, root: TreeNode, target: int) -> List[List[int]]:
if not root:
return []
stack = [(root, [root.val])]
res = []
while stack:
node, val = stack.pop()
if node and not node.left and not node.right and sum(val) == target:
res.append(val)
if node.left:
stack.append((node.left, val + [node.left.val]))
if node.right:
stack.append((node.right, val + [node.right.val]))
return res
LeetCode 1457. 二叉树中的伪回文路径
给你一棵二叉树,每个节点的值为 1 到 9 。我们称二叉树中的一条路径是 「伪回文」的,当它满足:路径经过的所有节点值的排列中,存在一个回文序列。
请你返回从根到叶子节点的所有路径中 伪回文 路径的数目。
示例 1: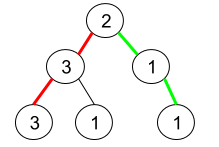
输入:root = [2,3,1,3,1,null,1]
输出:2
解释:上图为给定的二叉树。总共有 3 条从根到叶子的路径:红色路径 [2,3,3] ,绿色路径 [2,1,1] 和路径 [2,3,1] 。
在这些路径中,只有红色和绿色的路径是伪回文路径,因为红色路径 [2,3,3] 存在回文排列 [3,2,3] ,绿色路径 [2,1,1] 存在回文排列 [1,2,1] 。
解析:
如果集合中所有元素的某种排列是回文串,那么集合中最多有一种元素出现了奇数次。
那么题目就变成了统计所有根节点到叶子结点的路径中,符合上述特点的路径数量。
class Solution:
def pseudoPalindromicPaths (self, root: TreeNode) -> int:
self.arr = [0] * 10
self.count = 0
self.dfs(root)
return self.count
def dfs(self, root):
if not root:
return
self.arr[root.val] += 1
# 走到叶子结点进行出现次数的统计
if not root.left and not root.right:
odd = 0
for i in range(10):
if self.arr[i] % 2 != 0 and self.arr[i] != 0:
odd += 1
if odd < 2:
self.count += 1
if root.left:
self.dfs(root.left)
if root.right:
self.dfs(root.right)
self.arr[root.val] -= 1