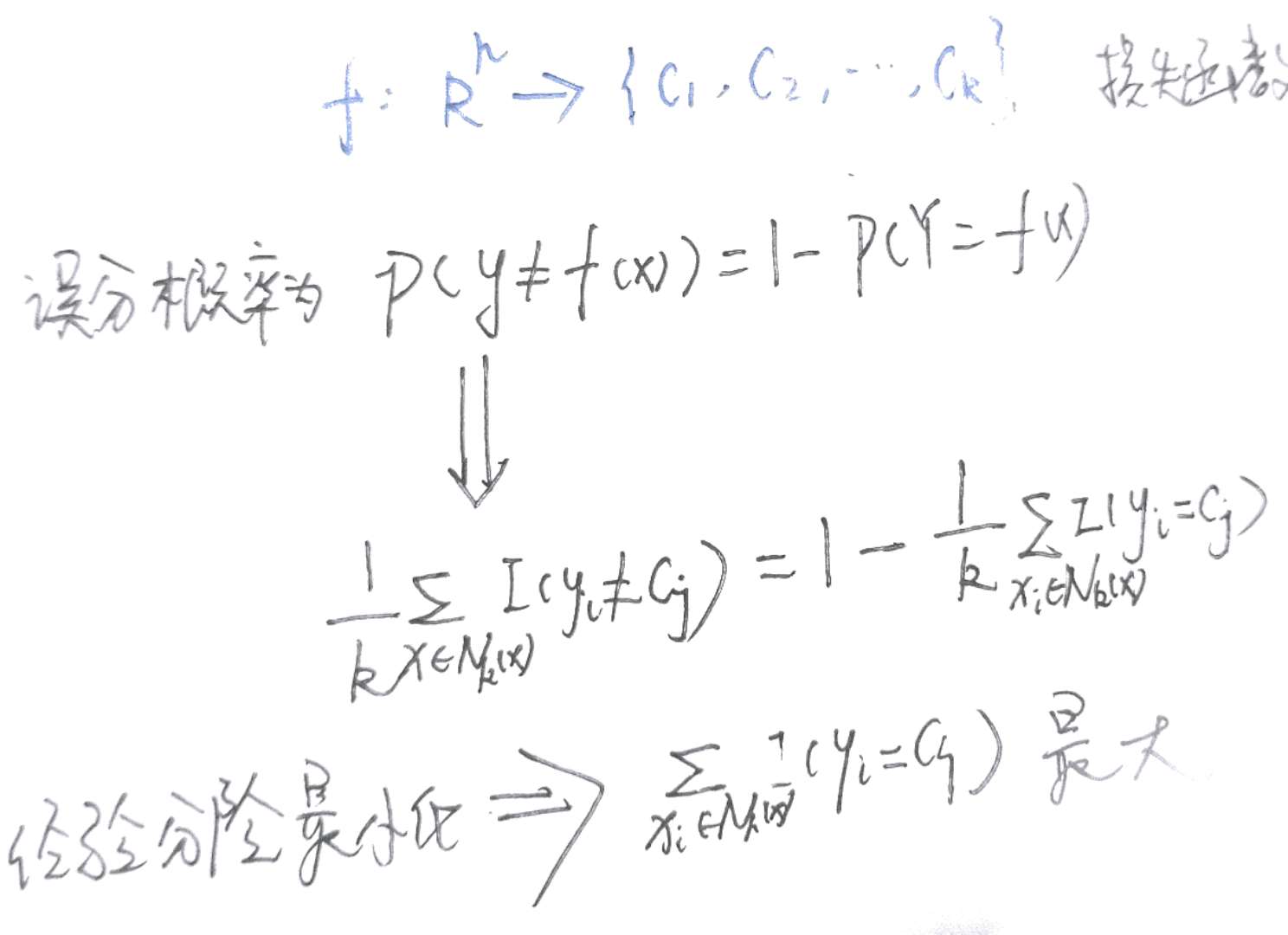机器学习之路——K邻近法详解

统计学习方法第三章——knn算法

首先要明确的第一个重点是，k邻近不具有显示的学习过程，它是基于实例的一种学习方法，简单来说就是给定一堆西瓜的数据，然后输入一个新西瓜的数据，找到与这个新西瓜最近的k个西瓜，这k个西瓜如果大多数是属于又甜又好吃的西瓜，那么就把这个西瓜分为又甜又好吃的西瓜这一类的西瓜中。

从上述的描述中不难看出，有三个要注意的一个是K值，也就是周围有几个西瓜和新西瓜相邻，如果k太小，那么好处是近似误差会减小，只有特征与这几个西瓜相似的才对预测新西瓜的“甜”“好吃”起作用，但是相同的，会带来一个问题，就是假如在这几个西瓜中不甜的多，那么会带来估计误差，这也就是k值减小使得模型变的复杂，复杂度上升，容易发生过拟合。k太大也就容易理解了，如下图

二是距离的度量，一般采用欧式距离，但也有不同的距离度量可供选择，不同的距离所确定的最近邻点不同。

1:a）

(1)曼哈顿距离：

(2)欧几里得距离：

(3)切比雪夫距离：

(4)闵可夫斯基距离：

(5)马氏(Mahalanobis)距离 ：

三是分类决策规则的不同，往往采用的策略是多数表决策略，如果采用的是多数表决策那么，我们可以进行如下推导：

接下来就是实践。我们来看一下不同的k值不同的分类决策对性能有什么影响。

对于经典的IRIS数据集我进行了如下实验

matlab代码如下：

%处理数据

data = X%数据集

forl=1:10 %进行10次实验；

[train,test] = crossvalind('Holdout', 150, 0.5);%实现随机分成按50%两个组一个训练集一个测试集

TrainData=data(:,train);

 TrainLabels=label(:,train);

 TestData=data(:,test);

TestLabels=label(:,test);

%knn算法核心

k=1;%k个近邻点（1，20，50）

error=0;

[M,N]=size(TrainData);

fori=1:N

 test=TestData(:,i)%每次从测试集中拿出一个实例进行计算

 forj=1:N

 distance(:,j)=test-TrainData(:,j);%计算他与训练集中每个数据的距离

 dis=sqrt(sum(distance.^2));%求距离

  [B ,IX] = sort(dis,'ascend');%排序

  len =min(k,length(B));%取最小的前k个

  resultLabel = mode(TrainLabels(IX(1:len)));%多数原则求众数

    end

      result(i)=resultLabel;%创建结果数组

 ifresult(i) ~= TestLabels(i)%结果数组与测试集相对比

     error =error+1;

 end

end

    rate(l)=1-error/N;%计算识别率

 end

      avrate=mean(rate(l));%计算平均识别率

forl=1:10

     fprintf('正确识别率为：%f \n',rate(l));

 end

fprintf('平均识别率为：%f',avrate);

随着k值增大识别率开始降低，当k值达到50时，识别率下降到50%左右。可能是算法出现了一些问题，但是由于我是用的50%的训练集 50%的测试集。

另一种knn算法实现直接调用matlab接口；

for i=1:10

a = double(X');    % Use all data for fitting  

    经过实验我发现，影响算法性能不只是k，距离的选择，还有决策方法这三个重要因素。数据特征的维数对算法影响很大，主要是在时间复杂度上，因此在高维数据上应当进行预先处理，比方说采用kd树，压缩近邻法等在空间内能快速搜索高维数据的办法，

   交叉验证也会影响，因为在看matlab自带的接口时，它所使用的k折交叉验证，而我使用的是简单交叉验证，这一定程度上影响着算法的泛化能力，虽然knn是基于实例的一种学习，但是对于有一定分布规律的数据，交叉验证的效果更好些。

补充知识：一.knn错误率与贝叶斯错误率关系

  二.不同的分类决策方法

  三.加快搜索的办法

下面介绍两种方法：

1.kd树为代表的树形结构：算法步骤：

1    在kd树种找出包含目标点x的叶结点：从根结点出发，递归地向下搜索kd树。若目标点x当前维的坐标小于切分点的坐标，则移动到左子结点，否则移动到右子结点，直到子结点为叶结点为止。

2   以此叶结点为“当前最近点”。

3    递归的向上回溯，在每个结点进行以下操作：

4 （a）如果该结点保存的实例点比当前最近点距离目标点更近，则更新“当前最近点”，也就是说以该实例点为“当前最近点”。

5 （b）当前最近点一定存在于该结点一个子结点对应的区域，检查子结点的父结点的另一子结点对应的区域是否有更近的点。具体做法是，检查另一子结点对应的区域是否以目标点位球心，以目标点与“当前最近点”间的距离为半径的圆或超球体相交：

6   如果相交，可能在另一个子结点对应的区域内存在距目标点更近的点，移动到另一个子结点，接着，继续递归地进行最近邻搜索；

7  如果不相交，向上回溯。

当回退到根结点时，搜索结束，最后的“当前最近点”即为x 的最近邻点。一般来说，样本数N>2^D(D是维数)时候才有效果

  2.位置敏感哈希法（LSH）：

   随着维数增加，任意两点之间最大距离与最小距离趋于相等，此时，常用的树索引方法将难以达到较好的效果。而LSH是基于随机映射算法，它将高维向量映射到低维空间，并且以较大的概率使映射前相近的点映射后仍然相近。LSH虽然采用近似的方法，不保证得出精确的结果，但是它能以较低的代价返回精确的或接近精确的结果。

原理：LSH建立了一种映射准则，将原始高维的数据空间S中的点映射到相对低维空间U，保证S中距离相近的点在U中距离也相近甚至相等，查询时将查询点做映射，映射到U中与之相近的点，找到的这些点的原象就是s中与查询点相近的点。因此映射的建立，空间的选择，空间的度量是LSH要专注的问题。

实现方案：

基于汉明空间的LSH

基于P-Stable的LSH