图解辗转相除法求解最大公约/最小公倍数

先上辗转相除法的三个代码实现：

#include <stdio.h>
#include <stdlib.h>

int gcd1(int a, int b)
{
    int ret;

    while(1)
    {
        if(a >= b)
        {
            a = a%b;
            if(a == 0)
            {
                ret = b;
                break;
            }
        }
        else
        {
            b = b %a;
            if(b == 0)
            {
                ret = a;
                break;
            }
        }
    }

    return ret;
}

int gcd2(int a,int b)
{
    if(b == 0)
        return a;
    return gcd2(b,a%b);
}

int gcd3(int a,int b)
{
    while(b){
        int t = b;
        b = a%b;
        a = t;
    }
    return a;
} 

int main(void)
{
    int a, b;
    
    a= 100;
    b = 45;

    printf("%s line %d, res1 %d, res2 %d, res3 %d.\n", __func__, __LINE__, gcd1(a, b), gcd2(a, b), gcd3(a, b));

    return 0;
}

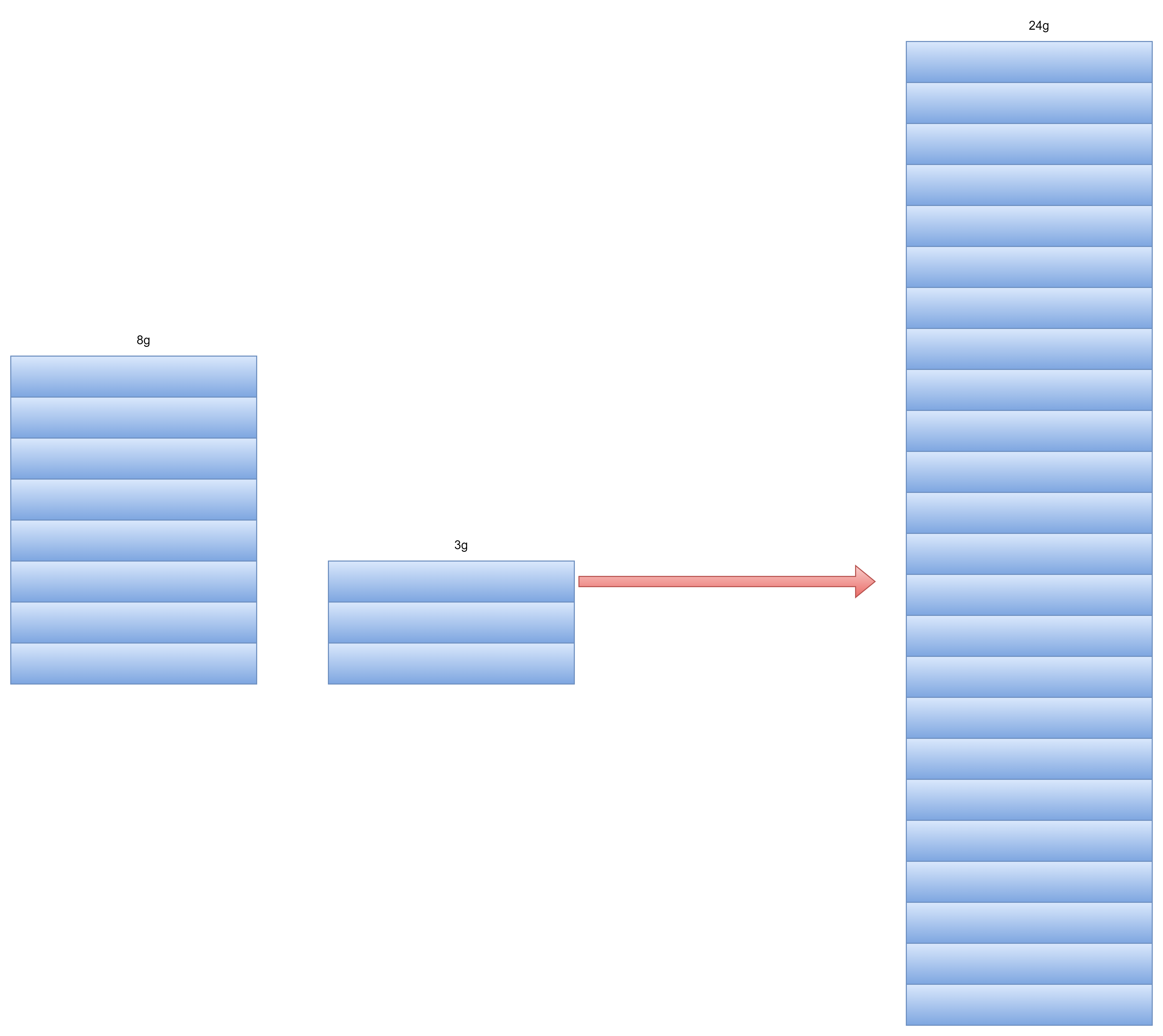
下面用一幅图示解题过程，图中蓝色的举行单元表示一个最小公约的单元。它具有以下性质：

1.以最小公约表示的两个原数字互质。（这是必然，反证法，如果不互质，则可以提取一个共同的因子重新定义最小公约单元，直到表示为互质，比如图中的8和3互质）。

2.辗转相除的每个阶段的两个数字也均互质，证明过程类似，反正法即可（当前辗转阶段如果存在共同的约数，则必然传递到之前的阶段也都有同样的约数，所以同理最小公约单元也要重新定义，直到每级辗转互质）。

基于以上两个严密的逻辑，辗转相除一定能够找到组成两个数字的最基本的公约块儿，它是两个数字共有的零件。

扩展-求最小公倍数

既然上一步已经计算得到了最小公约数，并且得到了以最小公约表示的两个原数字互质的推论，就不难得到计算最小公倍数的公用公式。

通用算法，已知数字m,n的最大公约数是g,则m/g, n/g互质，两个互质的数的最小公倍数就是两个质数之积，所以，最小公倍数为

$\frac{m}{g}\cdot \frac{n}{g} = \frac{mn}{g^2}$

由于单元为g,所以最小公倍数的真实值为：

$\frac{m}{g}\cdot \frac{n}{g}\cdot g = \frac{mn}{g^2}\cdot g = \frac{mn}{g}$

#include <stdio.h>
#include <stdlib.h>

int gcd1(int a, int b)
{
    int ret;

    while(1)
    {
        if(a >= b)
        {
            a = a%b;
            if(a == 0)
            {
                ret = b;
                break;
            }
        }
        else
        {
            b = b %a;
            if(b == 0)
            {
                ret = a;
                break;
            }
        }
    }

    return ret;
}

int gcd2(int a,int b)
{
    if(b == 0)
        return a;
    return gcd2(b,a%b);
}

int gcd3(int a,int b)
{
    while(b){
        int t = b;
        b = a%b;
        a = t;
    }
    return a;
} 

int lcm1(int a, int b)
{
	int g_c_d = gcd1(a, b);

	return a*b/g_c_d;
}

int lcm2(int m, int n)
{
	int mn, r ;
	
	if(m<n){
		mn = m ; 
		m = n ; 
		n = mn;
	}
	
	mn = m * n ;//俩个数的乘积
	r = m % n ;
	while(r!=0){
		m = n ;
		n = r ;
		r = m % n ;
	}
	return mn/n; //n为最大公约数
}

int main(void)
{
    int a, b;
    
    a= 100;
    b = 45;

    printf("%s line %d, res1 %d, res2 %d, res3 %d, lcm1 %d, lcm2 %d.\n", __func__, __LINE__, gcd1(a, b), gcd2(a, b), gcd3(a, b), lcm1(a, b), lcm2(a,b));

    return 0;
}

main line 84, res1 5, res2 5, res3 5, lcm1 900, lcm2 900.

图解：

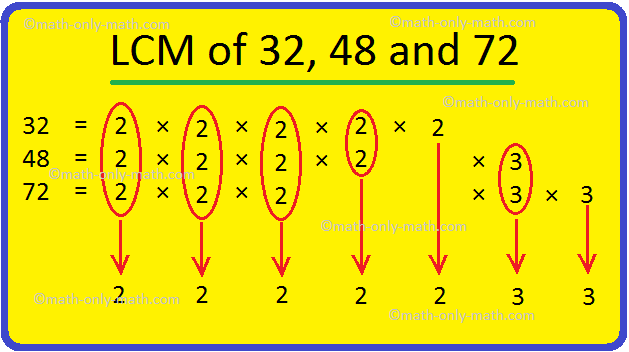
LCM of 32, 48 and 72 = 2 × 2 × 2 × 2 × 2 × 3 × 3 = 288

关于两个互质数的最小公倍数是两数之积，可以证明如下，假设a,b两数互质，也就是两数没有1以外的公约数，则最小公倍数是axb.

不失一般情况，假设a<b,则a的倍数从小到大排列为a,2a,3a,......(b-1)a, ba;在ba之前的所有a的倍数中，假设ka(1<k<b)同样也是b的倍数，则

$\frac{ka}{b}$

是整数。

由于a,b互质，则a/b不可能存在导致结果为整数的因子，所以只有k存在这个因子，但是k小于b,所以同样得到结论，这样的K不存在，这样，最小的公倍数只能是ab了，结论得证。

或者用反证法，我们知道ab一定是公倍数，要证明是最小，其它公倍数对最小公倍数之间一定可以整除（其他公倍数之间不一定），所以假设ab/n是其最小公倍数，则根据ab/n整除a,b可以推理出n是a,b的公因数，这和a,b互质矛盾。

总结：

基本原理：两个整数的最大公约数等于，其中较小的数和两数的差的最大公约数。

个人解析：若A、B有最大公约数K（A > B)，则，A、B、（A - B）、A mod B（A / B的余数），都是K的倍数。即余数（A - B）和 B 的最大公公约数也是 K 。

由此递归，可知当 A mod B = 0，即 A 是 B 的倍数时，此时，B 即为 K 。实际上，存在如下定理：

两数最大公约数与最小公倍数的积等于两数之积，用公式表示就是：

$gcd(p,q)\times lcm(p,q)=pq$

当

$gcd(p,q)=1$

时

$lcm(p,q)=pq$

最大公因数*最小公倍数=pq

结束

原文链接：https://blog.csdn.net/tugouxp/article/details/126820935