近期,小组成员为解决项目中的功能需求,查找了深度学习的相关书籍以及技术文献,并学习了神经网络与推荐算法的相关知识技术,为生成各个关键词对于各项职业的权重确定技术方向。
神经网络:
基本模块——神经元:
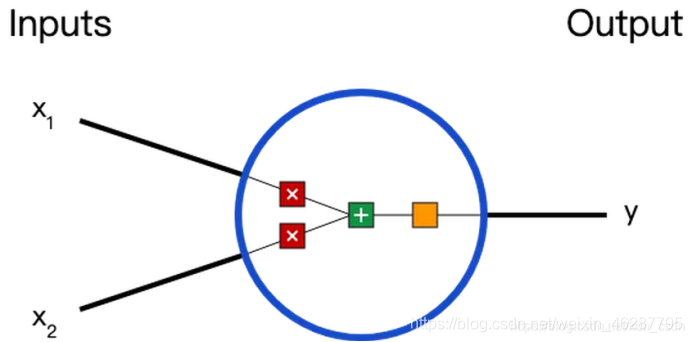
每一个连接都有各自的权重,如何对人工神经网络的权重进行初始化是一个非常重要的话题,这将会直接影响到之后的训练过程,以及最终整个模型的性能。连接的权重通常情况下是一些随机值,可以是负值,正值,非常小,或者非常大,也可以是零。和这个神经元连接的所有神经元的值都会乘以各自对应的权重,然后再把这些值都求和。
在这个神经元里,输入总共经历了3步数学运算:
- x1→x1∗w1
- x2→x2∗w2
- (x1∗w1)+(x2∗w2)+b
先将输入乘以权重(weight),再经过激活函数(activation function)处理得到输出:
- y=f((x1∗w1)+(x2∗w2)+b)
其中,激活函数的作用是将无限制的输入转换为可预测形式的输出。
搭建神经网络:
神经网络是神经元逐层组织以非循环的方式连接的图,也就是说,一些神经元的输出也可以变成另外神经元的输入,但神经网络中不允许环的出现。通常在神经网络中,层与层之间是以全连接(Fully-connected)的方式进行连接,相邻层之间的神经元都互相连接,相同层内的神经元之间不连接。如下图所示:
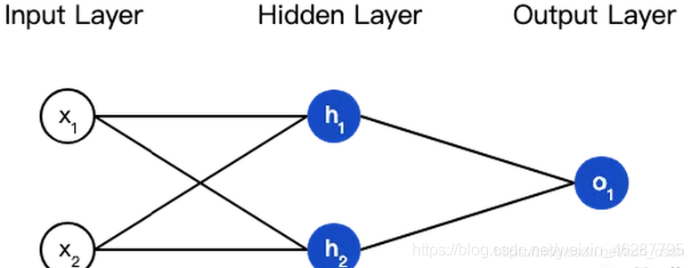
这个网络有2个输入、一个包含2个神经元的隐藏层(h1和h2)、包含1个神经元的输出层o1。隐藏层是夹在输入层和输出层之间的部分,一个神经网络可以有多个隐藏层。
把神经元的输入向前传递获得输出的过程称为前馈(feedforward)。
例如,令w1=0,w2=1,b=0,激活函数为sigmoid,则有:
- H1=h2=f(w*x+b)=f(3)
- O1=f(w1h1+w2x2+b)=f(0.9526)
神经网络的表示能力:
已经被证明,至少包含一个隐藏层的神经网络就可以近似任意的连续函数,可以参考文章Approximation by Superpositions of Sigmoidal Function。(http://www.dartmouth.edu/~gvc/Cybenko_MCSS.pdf)
随着网络规模的不断扩大,网络中的参数也就急剧增加,那么就会需要大量的数据来调整参数。当数据不多时,为了能使网络不仅对训练的数据更好的预测,也要对未知的数据具有良好的预测(通常把这种能力成为泛化能力(generalization ability)),就需要防止过拟合(over-fitting)现象的发生,过拟合就是对训练数据有很好的预测,而对未知数据的预测很差,如正则化(Regularzation),归一化(Normalization)。
推荐算法:
推荐系统的功能是帮助用户主动的找到满足偏好的个性化物品并推荐给用户。在本质上可以当做一个个性化的搜索引擎,输入的数据为用户行为信息、偏好信息等,返回的结果为最符合查询条件的物品列表。
它的数学化表示为:物品列表=f(用户偏好)。
而推荐引擎就扮演着这里的函数的角色,它主要需要完成两部分的工作:针对查询条件的相关性进行评估;筛选出符合条件的物品。即对上述函数进行计算。
然而现实上大多数推荐系统将上述计算分为两部分:推荐召回、推荐排序。推荐召回指在所有物品集合中检索到符合用户兴趣的候选集,大约筛选出几百个候选的列表;推荐排序的目的是要利用展示、点击(或转化)数据,然后加入更多的用户、物品特征,对推荐候选进行更精细的修正、打分。
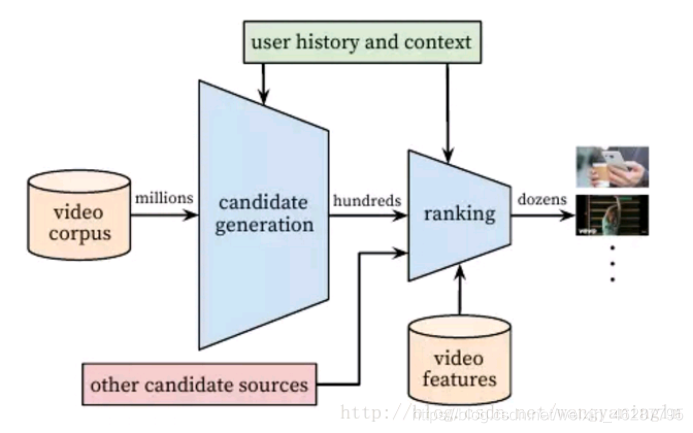
因此,推荐系统需要完成两步计算:候选集生成和排序,这两阶段的估计函数分别表示为g和h,即f=g(h(x))。
深度神经网络通过众多的简单线性变换层次性的进行非线性变换对于数据中的复杂关系能够很好的进行拟合,即对数据特征进行的深层次的挖掘。神经网络作为一种近似化求解方法可以用来对于公式f=g(h(x))的两个函数g,h进行近似。