Python中的数字有各种形状和形式。存在不同类型的数字表示的原因是因为它们都有不同的权衡。这些权衡通常令人惊讶!整数
关于整数的最令人惊讶的事情是它们停止成为整数的难易程度。例如,4/3将两个整数相除 得到一个浮点数,并且(4/3)*3是 float 4.0。即使程序没有浮点数输入,浮点数存在于某处所需的所有操作都是除法运算。浮点数
浮点数的行为不像数字。数字遵循某些数学特性:减法是加法的逆,加法是关联的,等等。
例如

将两个数字相加,然后一次相减一个,将不会得到相同的值。
他们不遵守加法的关联法则 a + (b + c) = (a + b) + c:

这些仅显示浮点数出现的两个极端情况,这可能令人惊讶。关于浮点行为可能令人惊讶的方式的完整论述太大了,不足以适合此文章的空白。分数
许多看起来简单明了的算法都会用精确的分数“爆炸”。爆炸通常从时间爆炸开始:算法变成“二次方”:花费的时间与输入长度不成正比,而与输入长度的惊吓成正比。换句话说,将输入大小加倍 会花费四倍的时间。
如果花费足够的时间,内存爆炸也是可能的:空间需求增加,直到所有内存都填满。
一种防止内存爆炸的怪异方法是,通常花很长时间才能获得它,并且该程序会因“挂起”而被杀死。
一种这样的“算法”是加法。

这只是将反数添加到一些素数中(我从列表中删除了前几个,然后将列表切成下一个10,000)。在设计成游戏平台的笔记本电脑上,一分钟内增加10,000个数字,结果输出超过90K!
相比之下,使用浮点数运行相同的算法效率更高:

花费的时间不到一毫秒,其中一些可能是datetime以来的测量误差 。这快了大约10,000倍。输出可以保存为17个字节:空间仅减少1000。但是,结果不准确:

结果相差不到1e-14。这就像将到月球的距离弄错了1毫米。在不涉及将火箭发射到月球的公差小于一毫米(一粒沙)的情况下,浮子的结果足够精确,效率更高几个数量级。
许多响应都是基于“分数很慢,因为分数是用Python实现的”。Python可能会导致速度降低10倍,而不是10,000倍。有一个第三方模块 quicktions,它使用Cython实现分数。
使用quicktions,的确是更快。在我的笔记本电脑上,时间从一分十六秒减少到一分十五秒。
从根本上讲,问题在于这是二次算法。我仔细选择了输入:小数加法的最坏情况是在质数上。但是,除非可以预测算法的输入,否则除了最坏的情况外,你将无法依赖其他任何东西。小数点
小数在管理金融交易时很有用。出于最无聊的原因,这可能是:财务法律以小数点表示。但是,Python中的所有小数点计算都由隐藏的全局状态控制:context。上下文决定了精度,它取材于对API远距离动作有问题的漫画。
引用文档 (对于Python 3.8):
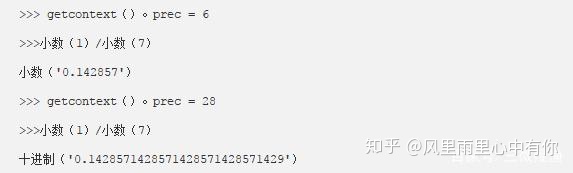
实际上,代码在设置精度和进行计算之间可能有数百行。计算可以在另一个函数中,甚至在另一个文件中。
在Python中使用十进制数字的唯一安全方法是 localcontext:

只要小心使用 localcontext,小数就可以很好地工作。它是线程安全的和信号安全的。摘要
在对代码中的数字进行处理之前,请停下来思考。你应该使用哪种类型?你想发生什么?哪些公差很重要?
不思考意味着让代码中的极端情况发生。
进阶学习资料获取方式:私信小编 “ 学习 ”,即可免费获取!



















领取方式:老规矩,直接私信小编 “ 学习 ”,即可获取啦!
谢谢大家的支持!