Description
 Background
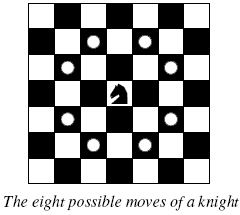
Background The knight is getting bored of seeing the same black and white squares again and again and has decided to make a journey
around the world. Whenever a knight moves, it is two squares in one direction and one square perpendicular to this. The world of a knight is the chessboard he is living on. Our knight lives on a chessboard that has a smaller area than a regular 8 * 8 board, but it is still rectangular. Can you help this adventurous knight to make travel plans?
Problem
Find a path such that the knight visits every square once. The knight can start and end on any square of the board.
Input
The input begins with a positive integer n in the first line. The following lines contain n test cases. Each test case consists of a single line with two positive integers p and q, such that 1 <= p * q <= 26. This represents a p * q chessboard, where p describes how many different square numbers 1, . . . , p exist, q describes how many different square letters exist. These are the first q letters of the Latin alphabet: A, . . .
Output
The output for every scenario begins with a line containing "Scenario #i:", where i is the number of the scenario starting at 1. Then print a single line containing the lexicographically first path that visits all squares of the chessboard with knight moves followed by an empty line. The path should be given on a single line by concatenating the names of the visited squares. Each square name consists of a capital letter followed by a number.
If no such path exist, you should output impossible on a single line.
If no such path exist, you should output impossible on a single line.
题意:n组数据,输入p*q代表棋盘的大小,p和q谁都可以是行或列,p按数字大小排序,q按大写字母排序,一个骑士在该棋盘上走“日”字步,问该骑士能否走遍该棋盘的每一个方格,如果能就按字典序大小输出其路径,如果字母相同则按数字升序输出其路径;如果不能走遍就输出“impossible”。
思路:由于行和列是自行定义的,则其八个方向走向的坐标也是自行定义的,只要让那八个方向坐标是按题目要求排序的即可,即让骑士先走的方向为字母和数字是最小的方向。
Sample Input
3 1 1 2 3 4 3
Sample Output
Scenario #1: A1 Scenario #2: impossible Scenario #3: A1B3C1A2B4C2A3B1C3A4B2C4
#include <cstdio>
#include <cstring>
using namespace std;
bool mmap[30][30];
int p,q;
int dx[]= {-2,-2,-1,-1,1,1,2,2}; //其八个方向的方向坐标
int dy[]= {-1,1,-2,2,-2,2,-1,1};
int xflag[100],yflag[100]; //记录其路径
int DFS(int x,int y,int ans) //让记录步数的ans当作参数,如果放在DFS函数里进行++那么步数会多加的,因为如果在当时++了,而该步不能再进行下去,回溯时步数并没有减少,那么到最后步数就会多,所以让ans当作参数可以避免这种错误发生
{
mmap[x][y]=true; //标记该步已经走过
if(ans==p*q) //如果步数达到了所有格数则说明骑士能走遍棋盘所有方格
return 1;
for(int i=0; i<8; i++) //遍历骑士的八个方向
{
int xx=x+dx[i];
int yy=y+dy[i];
if(xx>0&&xx<=q&&yy>0&&yy<=p&&!mmap[xx][yy])
{
xflag[ans]=xx; //记录路径
yflag[ans]=yy;
if(DFS(xx,yy,ans+1)) //接着走下一步
return 1;
}
}
mmap[x][y]=false; //当走完这一层之后取消该步的标记
return 0;
}
int main()
{
//freopen("lalala.text","r",stdin);
int n;
while(~scanf("%d",&n))
{
for(int k=1; k<=n; k++)
{
scanf("%d %d",&p,&q);
memset(mmap,0,sizeof(mmap));
memset(xflag,0,sizeof(xflag));
memset(yflag,0,sizeof(yflag));
printf("Scenario #%d:\n",k);
xflag[0]=1;
yflag[0]=1;
if(DFS(1,1,1))
{
for(int i=0; i<p*q; i++)
{
printf("%c%d",xflag[i]-1+'A',yflag[i]);
}
printf("\n\n");
}
else
printf("impossible\n\n");
}
}
return 0;
}<strong>
</strong>版权声明:本文为zhang_di233原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。