选择问题最常见的问题有:
- 1.1选最大
- 1.2同时选最大和最小的算法
- 1.3找第二大
- 2.选第k小(分治策略)
主要内容来自【北京大学】 算法设计与分析
1.1选最大
选择算法 统一描述:设L是n个算法的集合,从L中选出第k小的元素,1<=k<=n,当L中元素按从小到大排好序后,排在第k个位置的数,就是第k小的数。
下面介绍 顺序比较法
算法Findmax
输入:n个数的数组L
输出:max,k
max <- L[1]; k <- 1
for i <- 2 to n do //for循环执行n-1次
if max < L[i]
then max <- L[i]
k <- i
return max, k算法Findmax第二行,for循环执行n-1次,所以
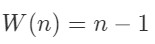
这个算法是选最大问题在时间上最优的算法(对于选最小问题,只需对算法稍加改动,就可以得到顺序比较的Findmin算法)
1.2同时选最大和最小的算法
设计思想:先选最大,然后把最大的从L中删除,接着选最小。
算法:(利用Findmax和Findmin)
输入:n个数的数组L
输出:max,min
if n=1 then return L[1]作为max和min
else Findmax
从L中删除max
Findmin算法执行的比较次数:
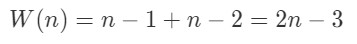
分组比赛的方法
基本思想:首先将L中的元素两两一组,分成
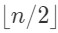
组(当n是奇数时有一个元素轮空)。每组中的2个元素进行比较,得到组内较大和较少数,把至多
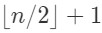
(当n为奇数时,把被轮空的元素加进来)个小组中较大的元素放在一起,运行Findmax,得到L中的最大元素,同理得到L中的最小元素。
算法FindMaxMin
将n个元素两两一组分成n/2(下取整)组
每组比较,得到n/2(下取整)个较小和n/2(下取整)个较大的数 //比较n/2(下取整)次
在n/2(下取整)个(n为奇数时,是n/2(下取整)+1)较小中找最小min
在n/2(下取整)个(n为奇数时,是n/2(下取整)+1)较大中找最大max行3和行4都执行
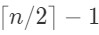
次,
所以
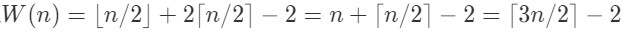
此算法效率更高,是所有同时找最大和最小算法中事件复杂度最低的算法。
1.3找第二大
2次调用Findmax算法
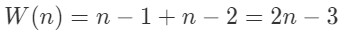
锦标赛算法
把数组中的元素两两一组,划分为
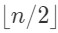
组(n为奇数时1个元素轮空),每组组内两个元素比大小,大的进入下一轮(n为奇数时,轮空的元素也进入下一轮)。 所以下一轮有
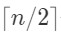
个元素。继续每组组内比大小,然后大的进入下一轮,直至找出max。筛掉n-1个元素,比较n-1次。
找第二大,不可能再用Findmax了,如果用Findmax,就又比较n-2次了,和上面的算法两次调用Findmax一样。 所以,我们可以利用找max时比较所产生的记录帮我们减少比较次数。在比赛前为每个元素设定一个指针,指向一个链表,把比较后比它小的元素都记录进它的链表中,找出max后,在max的链表中用Findmax找出整个数组第二大的元素。
算法FindSecond
输入:n个数的数组L
输出:second
k <- n
将k个元素两两一组,分成k/2(下取整)组
每组的两个数比较,找到较大的
将被淘汰的较小的数在淘汰它的数所指向的链表中做记录
if k为奇数 then k <- k/2(下取整)+1
else k <- k/2(下取整)
if k>1 then goto 2
max <- 剩下的一个数
second <- max的链表中的最大此时,第一轮两两比较的比较次数是n-1,但还不知道max的链表中有多少个元素, 所以接下来求解max所淘汰掉的元素个数(这部分的工作量) 设本轮参与比较的有t个元素,经过分组淘汰后进入下一轮的元素数至多是
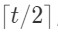
,下下一轮就是
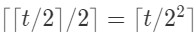
。
假设k轮淘汰后只剩max,则
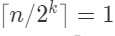
。
若n=2^d,那么
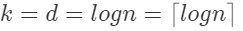
。
所以max进行了d次比较,
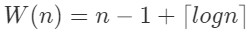
。 对于找第二大的问题,算法Findmax是时间复杂度最低的算法。
上面,我们只讨论了一些特例情况,基本上使用顺序比较或分组比较的方法,没有明确的分治算法的特征。下面考虑一般性的选第k小问题的算法,用到分治策略。
2.选第k小
输入:数组S,S的长度n,正整数k,1<=k<=n
输出:第k小的数
选第k小,可以使用排序算法,从小到大排好序后,选择第k个即可,最好的排序算法的时间复杂度是O(nlogn)。
下面考虑性能更好的分治算法,就是O(n)时间的算法,方便起见,假设数组S中元素彼此不等。
以S中的某个元素m*作为划分标准,将S划分为两个子数组S1和S2,把这个数组中比m*小的都放入S1的数组中,数组S1的元素个数是|S1|个;把这个数组中比m*大的都放入S2的数组中,数组S2的元素个数|S2|个。
- 若k<|S1|,则原问题归纳为在数组S1中找第k小的子问题。
- 若k=|S1|+1,则m*就是要找的第k小元素。
- 若k>|S1|+1,则原问题归纳为在数组S2中找第n-|S1|-1小的子问题。 算法的关键是如何确定这个划分S的标准m*,它要具有以下特征:
- 寻找m*的时间代价不能高于O(nlogn),如果直接寻找m*,时间应是O(n)。设选择算法的时间复杂度为T(n),递归调用这个算法在S上的一个真子集M上寻找m*,应该使用T(cn)时间(c<1,反映M的规模小于S)
- 通过m*划分的两个子问题的大小分别记作|S1|和|S2|,每次递归调用时,子问题规模与原问题规模n的比都不超过d(d<1),调用时间T(dn),并且应保证c+d<1,否则方程T(n)=T(cn)+T(dn)+O(n)的解不会达到O(n)。
下面的分治算法采用递归调用的方法寻找m*,先将S分组,5个元素一组,共分成
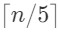
个组。
在每组中取中位数,把这
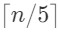
个中位数放入集合M中,然后使用选择算法选出集合M中的中位数m*。这次递归调用的子问题规模是原问题规模的1/5,1/5即为上文的特征(1)的c。
算法Select(S,k)
输入:数组S,S的长度n,正整数k,1<=k<=n
输出:第k小的数
将S划分成5个一组,共n/5(上取整)个组
每组中找一个中位数,把这些中位数放到集合M中
m* <- Select(M,|M|/2) //选M中的中位数m*,将S中的数组划分成A,B,C,D四个集合
把A和D中的每个元素与m*比较,小的构成S1,大的构成S2
S1 <- S1并C ; S2 <- S2并B
if k=|S1|+1 then 输出m*
else if k<=|S1|
then Select(S1,k)
else Select(S2,k-|S1|-1)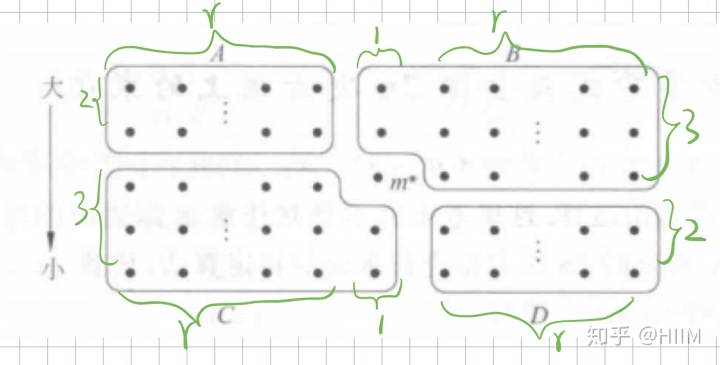
左下方的集合C中所以元素全部小于m*,右上角的集合B中的所有元素全部大于m*。仅仅对于A,D中的元素,我们不能确定它们是否大于或小于m*,所以在算法的行4加以比较,完成S1和S2的划分。
下面分析时间复杂度
假设n是5的倍数,且n/5是奇数,即n/5=2r+1,
所以|A|=|D|=2r,|B|=|C|=3r+2,n=10r+5。
若A,D的元素都小于m*,那么它们都加入至S1中,且下一步算法又在这个子问题上递归调用,这对应了归约后子问题的规模的上界,也正好是时间复杂度最坏的情况。类似的,如果A,D的元素都大于m*,也会出现类似的情况。 以前者为例时,子问题的大小是
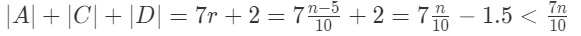
上式表明子问题规模最大不超过原问题的7/10,这个参数7/10就是前文特征(2)中的d。 所以最坏情况下的时间复杂度的递推式:
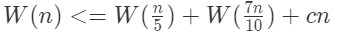
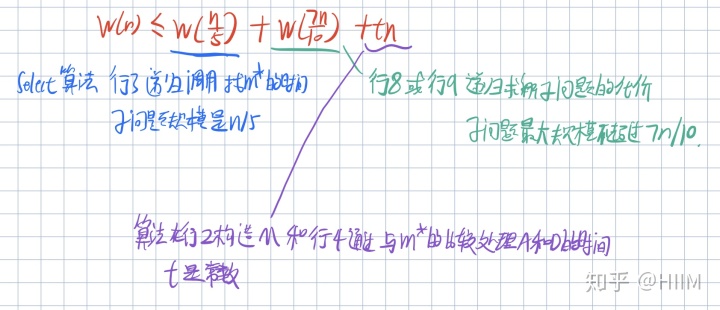
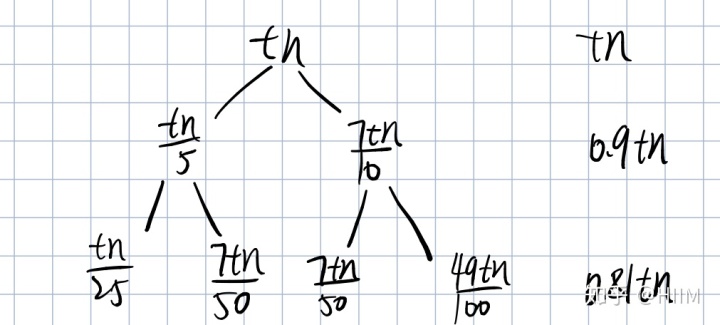
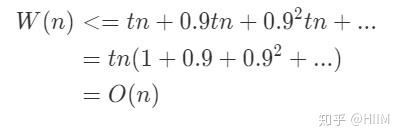
所以从上面的分析可以看出,这样找的m*完全满足算法要求,两次递归调用的参数分别是c=0.2,d=0.7,c+d=0.9<1。 所以Select算法可以把时间复杂度降至线性时间。 分组时也可以选3个或7个元素,元素数的改变可能会改变m*的特征,从而使得针对某些分组方法得到的c+d的值不再小于1,这就会增加运算时间。