01背包问题Java

题目
有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。

第 i 件物品的体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。

输入格式
第一行两个整数，N，V，用空格隔开，分别表示物品数量和背包容积。

接下来有 N 行，每行两个整数 vi,wi，用空格隔开，分别表示第 i 件物品的体积和价值。

输出格式
输出一个整数，表示最大价值。

数据范围
0<N,V≤1000
0<vi,wi≤1000
输入样例
4 5
1 2
2 4
3 4
4 5
输出样例：
8

问题解决：

（1）将题中输入举例转换成表格，清晰表现，后续计算帮助理解：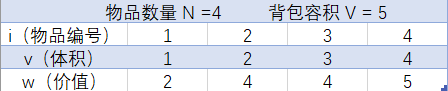

（2）总体思路：
动态规划
用子问题定义状态：即 f[i][v] 表示前 i 件物品恰放入一个容量为 v 的背包可以获得的最大价值。
则其状态转移方程便是：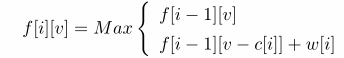

（3）01背包问题特点：每件物品仅有一件，选择放或不放
则该问题的子问题：前 i 件物品放入容量为 V 的背包中，考虑第 i 件物品放或不放。
每件物品只有两种状态：放与不放，而在前i件物品中已经选择好放那些物品，然后考虑第 i 件放或不放是否会有当前最大价值即最优解。

• 不放第i件物品：
  两种情况：1.背包剩余容积不足以装下第i件物品：则此时的价值与前i-1个物品价值一样： f[i][v] = f[i-1][v]；
  2.有足够的容积，但是装了第i件不一定会达到当前最大价值，因此要在装与不装之间作比较，选较大者：f[i][v] = max ( f[i-1][v]，f[i][v-c[i]]+w[i] )；若结果是 f[i-1][v] 则不放第i件物品。

• 放第i件物品：
  有足够的背包空间，并且选择放之后有当前最大价值，但同样直接作比较得出计算结果：f[i][v] = max ( f[i-1][v]，f[i][v-c[i]]+w[i] )；
  （4）根据状态转移方程可以将题中数据代入计算填表，进一步理解：

• 1.初始化：f[0][0] = 0;
  

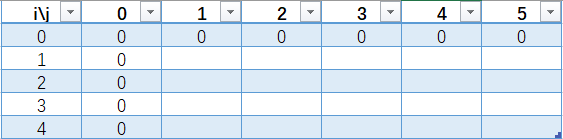
• 2.代入数据进行计算验证，如：
  i=1，j=1，w[1] = 2,v[1] = 1,j = v[1],f[1][1]= max ([f[1-1][1] , f[1-1][1-1]+2) ) = 2;
  一行一行的填表，得出结果，如下图 :
  
  得到最大价值为：f[N][V] = 8.

代码实现：

1.基本思路：

import java.util.Scanner;
public class Main {
    public static void main(String[] args) throws Exception {
        Scanner read1 = new Scanner(System.in);
        int N = read1.nextInt(); // 有N件物品；
        int V = read1.nextInt(); // 背包容量；
        int[] v = new int[N + 1]; //每件物品体积
        int[] w = new int[N + 1]; //每件物品价值
        for (int i = 1; i <= N; i++) {
            v[i] = read1.nextInt();
            w[i] = read1.nextInt();
        }
        read1.close();
        int[][] f = new int[N + 1][V + 1];
        f[0][0] = 0;
        for (int i = 1; i <= N; i++) {
            for (int j = 0; j <= V; j++) {
                f[i][j] = f[i-1][j];
                if(j >= v[i])  //判断背包容积是否足以装下该件物品
                {
                     f[i][j] = Math.max(f[i-1][j], f[i-1][j - v[i]] + w[i]);
                }  
            }
        }
        System.out.println(f[N][V]);
    }
 }

2.空间复杂度优化：

import java.util.Scanner;
public class Main {
    public static void main(String[] args) throws Exception {
        Scanner read1 = new Scanner(System.in);
        int N = read1.nextInt(); // 有N件物品；
        int V = read1.nextInt(); // 背包容量；
        int[] v = new int[N + 1]; //每件物品体积
        int[] w = new int[N + 1]; //每件物品价值
        for (int i = 1; i <= N; i++) {
            v[i] = read1.nextInt();
            w[i] = read1.nextInt();
        }
        read1.close();
        int[] f = new int[V + 1];
        f[0] = 0;
        for (int i = 1; i <= N; i++) {
            for (int j = V; j >= v[i]; j--) {  //此处是逆序（在完全背包问题中讲解为何）
                f[j] = Math.max(f[j], f[j - v[i]] + w[i]);
            }
        }
        System.out.println(f[V]);
    }
 }