树的直径
定义
直径 : 在圆上两点(不相交)之间最远的距离就是我们通常所说的直径。
树的直径 : 树上最远的两个节点之间的距离就被称为树的直径,连接这两点的路径被称为树的最长链
(一开始,下意识地以为是,找到某个节点到它子树中叶子节点的最大距离,显然不是)
法一、两次dfs、bfs
思想
先从任意一点P出发,找离它最远的点Q,再从点Q出发,找离它最远的点W,W到Q的距离就是是的直径。
证明
①若P已经在直径上,根据树的直径的定义可知Q也在直径上且为直径的一个端点(从直径的一个端点Q出发,距离Q最远的点就是直径的另一个端点)
树上任意点能到的最远点,一定是树的直径的某个端点。
②若P不在直径上,我们用反证法,假设此时WQ不是直径,AB是直径
1、若AB与PQ有交点C,由于P到Q最远,那么PC+CQ>PC+CA,所以CQ>CA,易得CQ+CB>CA+CB,即CQ+CB>AB,与AB是直径矛盾,不成立,如下图(其中AB,PQ不一定是直线,画成直线是为了方便)
2、若AB与PQ没有交点,M为AB上任意一点,N为PQ上任意一点。首先还是NP+NQ>NQ+MN+MB,同时减掉NQ,得NP>MN+MB,易知NP+MN>MB,所以NP+MN+MA>MB+MA,即NP+MN+MA>AB,与AB是直径矛盾,所以这种情况也不成立,如下图:
优点
== 可以有效处理 负边权==
缺点
对于记录路径的信息效率较低
实现代码
#include<iostream>
#include <algorithm>
using namespace std;
const int N=4e4+10;
struct edge{
int to,w,nex;
}e[N<<1];
int head[N];
int cnt;
void add(int u,int v,int w){
e[++cnt].to=v;
e[cnt].w=w;
e[cnt].nex=head[u];
head[u]=cnt;
}
int Q;//通过节点1找到的直径的一个端点
int ans;//找节点1/Q到 其子树根节点的最大距离
int d[N];//1每个节点到其
//这里不是 要求x到其子树根节点的最大距离(树形dp),
//而是距离1/Q距离最大的节点
//要求距离x节点最远的节点,可以用d[y]记录它的所有能蔓延出去的节点
//到x的距离
//这样一来,距离最大的那个节点就是要找的节点
//int vis[N];本来想优化dfs,找x的所有能到达的节点嘛
//但由于两节点之间只有一条路径(树),dfs下去不会重复,
//况且已经限制不能向上遍历了(向父亲)
void dfs(int u,int fa){
if(d[u]>ans){
ans=d[u];//最大距离
Q=u;//距离最初的u最远的节点
}
//反正可以通过d数组记录路径信息,可以dfs求出x所有能蔓延出去的节点
//到x的最远距离之后,d数组中最大元素对应的节点就是距离x最远的节点
for(int i=head[u];i;i=e[i].nex){
int to=e[i].to;
int w=e[i].w;
if(to==fa)continue;//无向边,不要陷入循环了
d[to]=d[u]+w;//对于d数组,有点从上到下推的味道,so在dfs前
dfs(to,u);
}
}
int main() {
int n,m;
cin>>n>>m;
// 道路不会交叉且每个农场间有且仅有一条路径
// m只会是n-1
int u,v,w;
char dir;
for(int i=1;i<n;i++){
cin>>u>>v>>w>>dir;
add(u,v,w);
add(v,u,w);
}
dfs(1,0);//默认n个节点的编号分别为1~n,0当作根节点不存在的父节点
// for(int i=1;i<=n;i++){
// if(d[i]>ans){
// ans=d[i];
// Q=i;
// }
// }
fill(d+1,d+1+n,0);
fill(vis+1,vis+1+n,0);
ans=0;
dfs(Q,0);
// for(int i=1;i<=n;i++){
// if(d[i]>ans){
// ans=d[i];
// Q=i;
// }
// }
cout<<ans;
return 0;
}
法二、树形dp
思想
1、先求出所有节点到其子树中叶子节点的最大距离d[x],
再对于每一个节点x,分别求出 d [ x ] + m a x ( d [ y i ] + e d g e [ y i ] ) d[x]+max(d[y_i]+edge[y_i])d[x]+max(d[yi]+edge[yi])
取每个节点得出结果的最大值
2、对于每一个节点x,求出x到其子树中叶子节点的最大距离f1[x],次长距离f2[x],
取每个节点得出f1[x]+f2[x]的最大值
对于每个节点我们要记录两个值:
f1 [ i ] 表示以 i 为根的子树中,i 到叶子结点距离的最大值
f2 [ i ] 表示以 i 为根的子树中,i 到叶子结点距离的次大值
对于一个节点,它到叶子结点距离的最大值和次大致所经过的路径肯定是不一样的
若j是i的儿子,那么(下面的 w [ i ][ j ] 表示 i 到 j 的路径长度):
若 f1 [ i ] < f1 [ j ] + w [ i ][ j ],f2 [ i ] = f1 [ i ],f1 [ i ] = f1 [ j ] + w [ i ][ j ];
否则,若 f2 [ i ] < f1 [ j ] + w [ i ][ j ],f2 [ i ] = f1 [ j ] + w [ i ][ j ];
理解:这样做就是,先看能否更新最大值,若能,它的次大值就是原先的最大值,再更新它的最大值;若不能,就看能不能更新次大值,若能,就更新,不能就不管它
这样的话,最后的答案 answer = max { f1 [ i ] + f2 [ i ] }
证明
我们不妨设1号点为根节点,那么这就可以看做一棵有根树。(设1号节点为根节点,那么一张N个点,N−1条边的无向图,我们可以认为它是一棵有根树)
1、可以求出从任意节点x出发,到以x为根的子树,能过到达最远节点(叶子节点)的距离
设D[x]表示从节点x出发,往以x为根的子树走,能够到达的最远距离。设x的子节点分别为y 1 , y 2 , y 3 , . . . , y t , e d g e ( x , y ) y1,y2,y3,...,yt,edge(x,y)y1,y2,y3,...,yt,edge(x,y)表示从x到y的边权,则可以得到状态转移方程:D [ x ] = m a x ( D [ y i ] + e d g e ( x , y i ) ) D[x]=max(D[yi]+edge(x,yi))D[x]=max(D[yi]+edge(x,yi))
2、有了第一步求出的每个节点到自己子树中叶子节点的最大距离,我们考虑对于每个节点x求出经过x的最长链的长度F[x],整棵树的直径就是m a x F [ x ] ( 1 < = x < = n ) max{F[x]}(1<=x<=n)maxF[x](1<=x<=n)。
现在我们考虑如何求F [ x ] 。 F[x]。F[x]。
对于x节点的任意两个子节点y i 和 y j y_i和y_jyi和yj,经过节点x的最长链的长度可以通过四个部分来构成:
D [ y i ] D[y_i]D[yi]
D [ y j ] D[y_j]D[yj]
从 x 到 y i 的 距 离 从x到y_i的距离从x到yi的距离
从 x 到 y j 的 距 离 从x到y_j的距离从x到yj的距离
不 妨 设 j < i , 则 有 : 不妨设j<i,则有:不妨设j<i,则有:
F [ x ] = m a x ( D [ y i ] + D [ y j ] + e d g e ( x , y i ) + e d g e ( x , y j ) ) F[x]=max(D[y_i]+D[y_j]+edge(x,y_i)+edge(x,y_j))F[x]=max(D[yi]+D[yj]+edge(x,yi)+edge(x,yj))
非常需要理解的一点,不管是贪心思想还是数学证明,都需要直到,对于经过节点x的最长链的长度(直径是所有节点的最长链中的最大值),是
m a x ( x 经 过 子 节 点 y i 到 达 其 子 树 叶 子 节 点 的 最 大 值 + x 经 过 子 节 点 y j 到 达 其 子 树 叶 子 节 点 的 最 大 值 ) max(x经过子节点y_i到达其子树叶子节点的最大值+ x经过子节点y_j到达其子树叶子节点的最大值)max(x经过子节点yi到达其子树叶子节点的最大值+x经过子节点yj到达其子树叶子节点的最大值)(可表示为
x到其子树叶子节点的最大值+ m a x ( x 的 子 节 点 y i 到 其 子 树 叶 子 节 点 的 最 大 值 + e d g e ( x , y j ) ) max(x的子节点y_i到其子树叶子节点的最大值+edge(x,y_j))max(x的子节点yi到其子树叶子节点的最大值+edge(x,yj))
显然,x到达其子树叶子节点的最长路径+次长路径
x到叶节点最长的两条路径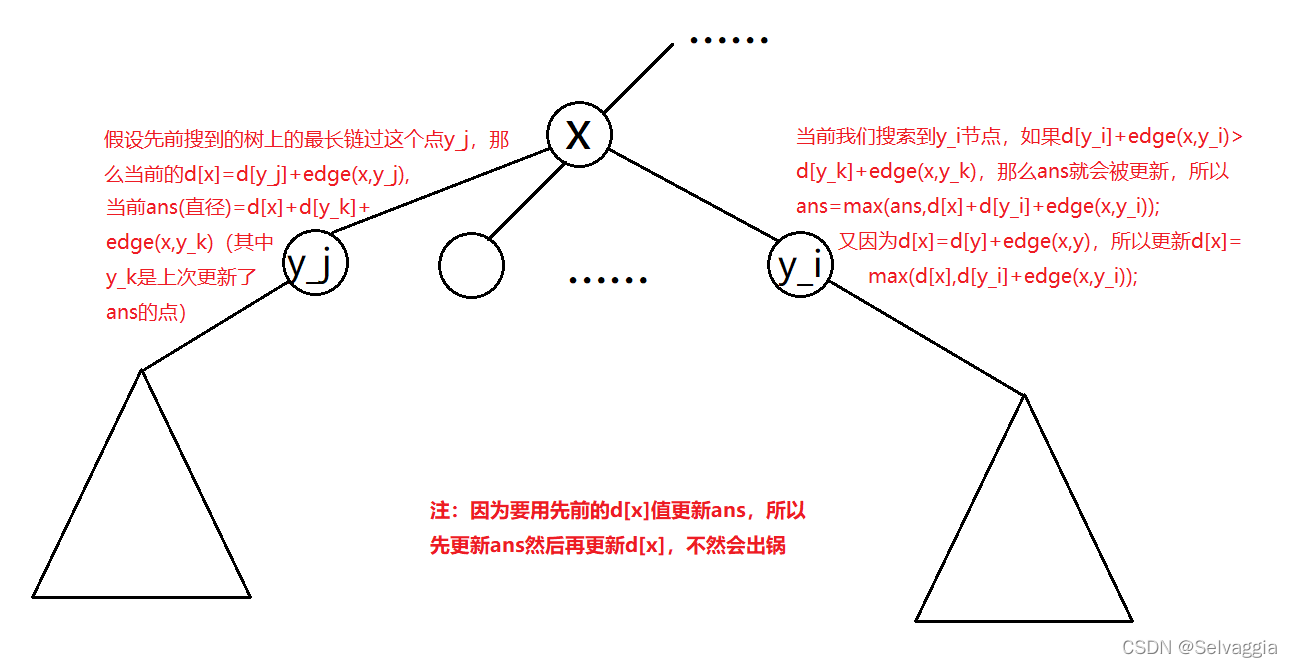
优点
可以通过一个新的数组记录路径信息(例如父节点与子节点之间的关系)
缺点
== 缺点 : 无法处理 负边权(遇到 负边权 凉凉)==
代码一 m a x ( 最 长 链 + 次 长 链 ) max(最长链+次长链)max(最长链+次长链)
#include<iostream>
#include <algorithm>
using namespace std;
const int N=4e4+10;
struct edge{
int to,w,nex;
}e[N<<1];
int head[N];
int cnt;
void add(int u,int v,int w){
e[++cnt].to=v;
e[cnt].w=w;
e[cnt].nex=head[u];
head[u]=cnt;
}
int f1[N];
int f2[N];
//f1,f2分别代表节点x到其子树节点的最大值和次大值
//两次dfs求直径中d数组是x节点能蔓延出去的所有节点到x的距离,应从上往下递推
//f1,f2显然应该从下往上递推
int ans;//直径=max( d[u]
void dfs(int u,int fa){
for(int i=head[u];i;i=e[i].nex){
int to=e[i].to;
int w=e[i].w;
if(to==fa)continue;
dfs(to,u);
if(f1[u]<f1[to]+w){
f2[u]=f1[u];//f2是次大值嘛,继承最大值上一次更新的值
f1[u]=f1[to]+w;
}
else f2[u]=f1[to]+w;
ans=max(ans,f1[u]+f2[u]);
}
}
int main() {
int n,m;
cin>>n>>m;
// 道路不会交叉且每个农场间有且仅有一条路径
// m只会是n-1
int u,v,w;
char dir;
for(int i=1;i<n;i++){
cin>>u>>v>>w>>dir;
add(u,v,w);
add(v,u,w);
}
dfs(1,0);
cout<<ans;
return 0;
}
代码二max(x到子树叶子节点最长路径+x某子节点到子树叶子节点最长路径+x到该子节点距离)记得更新每个节点到子树叶子节点的最长距离
#include<iostream>
#include <algorithm>
using namespace std;
const int N=4e4+10;
struct edge{
int to,w,nex;
}e[N<<1];
int head[N];
int cnt;
void add(int u,int v,int w){
e[++cnt].to=v;
e[cnt].w=w;
e[cnt].nex=head[u];
head[u]=cnt;
}
int f1[N];
//int f2[N];
//f1,f2分别代表节点x到其子树节点的最大值和次大值
//两次dfs求直径中d数组是x节点能蔓延出去的所有节点到x的距离,应从上往下递推
//f1,f2显然应该从下往上递推
int ans;//直径=max(f1[u]+f2[u])或max(f1[u]+f1[to]+w[u->to])
void dfs(int u,int fa){
for(int i=head[u];i;i=e[i].nex){
int to=e[i].to;
int w=e[i].w;
if(to==fa)continue;
dfs(to,u);
// if(f1[u]<f1[to]+w){
// f2[u]=f1[u];//f2是次大值嘛,继承最大值上一次更新的值
// f1[u]=f1[to]+w;
// }
// else f2[u]=f1[to]+w;
// ans=max(ans,f1[u]+f2[u]);
ans=max(ans,f1[u]+f1[to]+w);
f1[u]=max(f1[u],f1[to]+w);
// 在逐一遍历x的各子节点过程中,随时可能发现一条更长的
// x到其子树叶子节点的路,要更新f1[u]
// 因为 ans=max(ans,f1[u]+f1[to]+w)这个定义中
// f1[x]就是x到其子树叶子节点的最长路
}
}
int main() {
int n,m;
cin>>n>>m;
// 道路不会交叉且每个农场间有且仅有一条路径
// m只会是n-1
int u,v,w;
char dir;
for(int i=1;i<n;i++){
cin>>u>>v>>w>>dir;
add(u,v,w);
add(v,u,w);
}
dfs(1,0);
cout<<ans;
return 0;
}
题目集
以上给出的代码对应的就是这道板子题
些许离谱,oj上的题面似乎不完整,连数据范围都没有
完整题面如下
【问题描述】
农夫约翰有N个农场,标号为1到N。M条不同的垂直或水平的道路连接着农场,道路的长度不超过1000。这些农场的分布就像下面的地图一样,图中农场用F1…F7表示:
每个农场最多能在东西南北四个方向连接4个不同的农场。此外,农场只处在道路的两端。道路不会交叉且每个农场间有且仅有一条路径。但是约翰丢了农场的地图,他只得从电脑的备份信息中修复了。每一条道路信息描述如下:
从农场23往南经距离10到达农场17
从农场1往东经距离7到达农场17
……
最近美国过度肥胖非常普遍,农夫约翰为了让他的奶牛多做运动,举办了奶牛马拉松。马拉松路线要尽量长,请帮助约翰寻找两个最远的农场间的距离。
【输入格式】
第1行两个整数N和M。
第2到第M+1行:每行包括4个分开的整数:F1,F2,L,D分别描述两个农场的编号,道路的长度,F1到F2的方向N,E,S,W。
【输出格式】
一个整数,表示最远两个农场的距离。
【输入样例】
7 6
1 6 13 E
6 3 9 E
3 5 6 S
4 1 3 N
2 4 20 W
4 7 2 S
1
2
3
4
5
6
7
【输出样例】
51
1
【样例解释】
最长的马拉松路线通过4,1,6,3到5;总长为:20+3+12+9+7=32。
【数据范围】
1<=N,M<=40000
环游世界
题意:
切断树的一条边,将树分为两棵,要让两棵树的最长路径(即直径)中较大的那个最小。

#include<iostream>
#include<vector>
#include <math.h>
using namespace std;
const int N=1e6+5;
struct edge{
int to,nex,w;
}e[N<<1];
int head[N];
int cnt;
void add(int u,int v,int w){
e[++cnt].to=v;
e[cnt].w=w;
e[cnt].nex=head[u];
head[u]=cnt;
}
int Q,R;
int d[N];//每个节点到p的最远距离
int maxd;//存放最长的距离啦
void dfs(int u,int fa){
if(d[u]>maxd){
maxd=d[u];
Q=u;
}
for(int i=head[u];i;i=e[i].nex){
int to=e[i].to;
int w=e[i].w;
if(to==fa)continue;
d[to]=d[u]+w;
dfs(to,u);
}
}
bool fg=false;
//dfsPath会深搜很多条路径,但只需要保存直径这条路径上的边
//怎么判断深搜的这条边是直径,
//1、这条路最后一个节点是R 2、这条路的长度为之前算出的maxd
vector< pair<int,int> >v;
void dfsPath(int Q,int fa){
if(Q==R){
fg=true;
return;
}
for(int i=head[Q];i;i=e[i].nex){
int to=e[i].to;
int w=e[i].w;
if(to==fa)continue;
v.push_back(make_pair(Q,to));//顺序有讲究,断开这条边,pair左边的节点是在Q所属的那颗子树里
dfsPath(to,Q);
if(fg)return;
v.pop_back();
//不这条路是直径啦 ,这一路走来所有保存的边都要抛除去
}
}
//树形dp求每一棵子树的直径
//通过每个节点到其子树叶子节点的最大距离(最长链而不是最长路径,直径)
int f[2][N];//记录每个节点到其子树叶子节点的最大距离,最长链
//int mx;求树的直径板子题里,就是求给定的一棵树的直径,
//mx相当于mx[root],以root为根的最长路径,直径,用一个遍历mx足矣
//但这里要求,求以任意节点为根的子树的直径(以删除的边的两节点为根,删除的边是任意的)
int mx[2][N];//回顾一下mx的求法
//1、mx=max(mx,f[u]+f[v]+w),f[u]=max(f[u],f[v]+w)
//2、f1[u]或f2[u]=f[v]+w,mx=max(mx,f1[u]+f2[u]);
//注意啦,f[i]是i到其子树叶子的最长路径
//mx[i]是以i为根的树的最长链即直径(是i到叶子的最长路径+次长路径)
void dfs2(int u,int fa,int flag){//Q所在的半颗子树的众多子树的最长链
// mx[flag][u] = f[flag][u] = 0;
for(int i=head[u];i;i=e[i].nex){
int to=e[i].to;
int w=e[i].w;
if(to==fa)continue;
dfs2(to,u,flag);
mx[flag][u]=max(mx[flag][u],f[flag][u]+f[flag][to]+w);
f[flag][u]=max(f[flag][u],f[flag][to]+w);
//随着遍历u的各孩子,要更新u到叶子的最长链
}
//要与u所有的子树中最大直径比较,原来只用一个全局变量ans,即mx[root]
//ans在每一层递归中都会在与求出来的最长路径比较
//而今用mx数组代替ans,一来可以表示以每个节点为根的子树直径,但
//mx[u]已经不能再全局比较
//so递归的过程中u必须与它的孩子的最长路径比较,因为它的孩子
//已经与孩子的孩子进行了比较,握住了自他以下的最长路径
for(int i=head[u];i;i=e[i].nex){
int to=e[i].to;
mx[flag][u]=max(mx[flag][u],mx[flag][to]);
}
}
//void dfs2(int u,int fa,int flag)
//{
// int mx1=0,mx2=0;
// for(int i=head[u];i;i=e[i].nex){
// int v=e[i].to;
// int w=e[i].w;
// if(v==fa)continue;
// dfs2(v,u,flag);
// int t=f[v][flag]+w;
//
// if(t>=mx1) mx2=mx1,mx1=t;
// else if(t>mx2) mx2=t;
//
// f[u][flag]=max(f[u][flag],f[v][flag]+w);
// mx[u][flag]=max(mx[u][flag],mx[v][flag]);
// }
// //if(!flag) printf("u:%d mx1:%d mx2:%d\n",u,mx1,mx2);
// mx[u][flag]=max(mx[u][flag],mx1+mx2);
//}
int main() {
//最大距离的最小值,一定要切断直径,即删除的边在直径上(要保存直径这条路径)
//切断一条边后,变成两颗树,要求这两棵树中所有的子树的最长直径
ios::sync_with_stdio(false);
cin.tie(0);
int n;
cin>>n;
int x,y,w;
for(int i=0;i<n-1;i++){
cin>>x>>y>>w;
add(x,y,w);
add(y,x,w);
}
//1、欲遍历直径上的所有边,先找到直径的两端点
//两次dfs求直径(距离p最远的点Q是直径一个端点,距离Q最远的点是另一个端点R)
dfs(1,0);
fill(d+1,d+1+n,0);
maxd=0;
R=Q;//先保存一个端点
dfs(Q,0);
dfsPath(Q,0);
int len=v.size();
dfs2(Q,0,0);//dfs2用于求以每个节点为根节点的子树的最长路径
// 但随着割断的边不同,每个节点指不定属于Q,R哪一边
// 属于两边的情况都要求,第三个参数用于标记该节点属于哪一边时的直径
dfs2(R,0,1);
int res=0x3f3f3f3f;//要搞无穷大就要写齐4个3f啦,不然直接1e9
for(int i=0;i<len;i++){
int temp=max(mx[1][v[i].first],mx[0][v[i].second]);
res=min(res,temp);
}
cout<<res;
return 0;
}