1.原理部分
softmax与SVM结构类似。在Softmax分类器中,函数映射保持不变,但将这些评分值视为每个分类的未归一化的对数概率,并且将折叶损失(hinge loss)替换为交叉熵损失(cross-entropy loss)。公式如下:
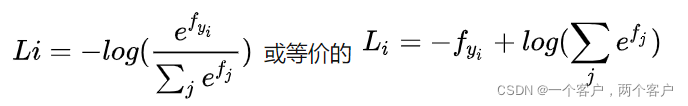
其中是正确标签预测值,
是其他预测值。
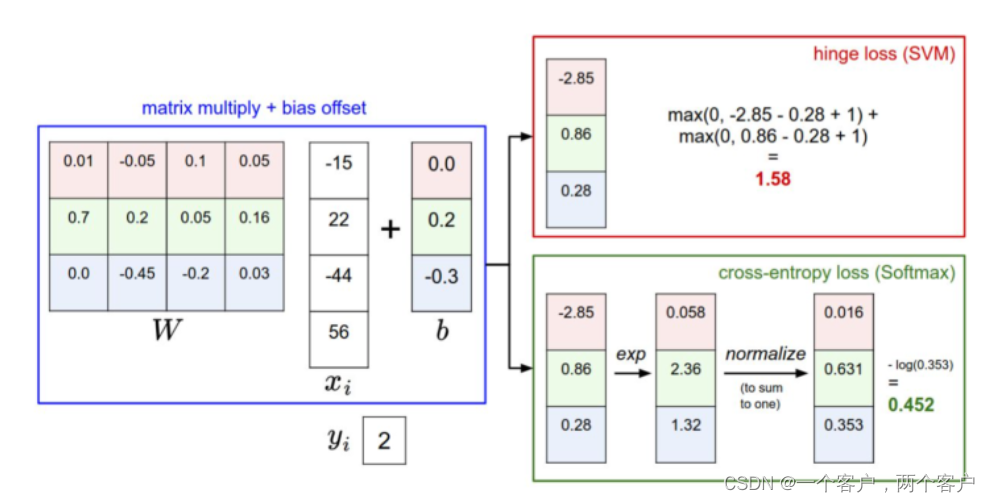
SVM与Sfotmax对比图如下:
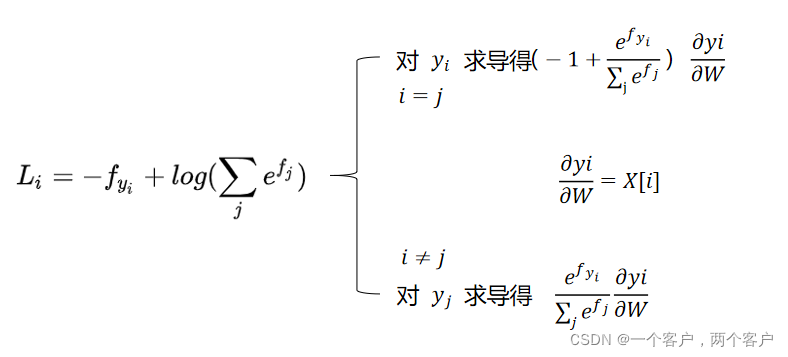
反向传播公式为:
2.损失函数代码实现
损失函数编写在cs231n/classifiers/softmax.py文件中
Softmax 损失函数,一般实现
输入的维度为 D,有 C 类,我们在 minibatch 上操作 N 个例子。
输入:
- W: 维度为(D, C) 的向量,代表权重值
- X: 维度为 (N, D)的向量,代表训练数据
- y: 维度为(N,) 的向量,代表训练标签; y[i] = c means
that X[i] has label c, where 0 <= c < C.
- reg: (float) 正则化强度
需要返回值:
- loss as single float
- gradient with respect to weights W; an array of same shape as W
def softmax_loss_naive(W, X, y, reg):
# Initialize the loss and gradient to zero.
loss = 0.0
dW = np.zeros_like(W)
#############################################################################
# TODO: Compute the softmax loss and its gradient using explicit loops. #
# Store the loss in loss and the gradient in dW. If you are not careful #
# here, it is easy to run into numeric instability. Don't forget the #
# regularization! #
#############################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
num_train = X.shape[0]
num_classes = W.shape[1]
F = X.dot(W)
normalized_F = (F.T - np.max(F, axis=1)).T # 标准化,这一步非必须
exp_normalized_F = np.exp(normalized_F) # 标准化后的exp
# compute loss
for i in range(num_train):
s_yi = exp_normalized_F[i][y[i]]
sum_i = np.sum(exp_normalized_F[i])
loss -= np.log(s_yi*1.0 / sum_i)
loss /= num_train
loss += reg*np.sum(np.square(W))
# compute dW
for i in range(num_train):
sum_i = np.sum(exp_normalized_F[i])
for j in range(num_classes):
dW[:, j] += (exp_normalized_F[i][j]*1.0 / sum_i)*X[i]
if j == y[i]:
dW[:, j] -= X[i]
dW /= num_train
dW += 2*reg*W
pass
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
return loss, dW向量形式为:
def softmax_loss_vectorized(W, X, y, reg):
"""
Softmax loss function, vectorized version.
Inputs and outputs are the same as softmax_loss_naive.
"""
# Initialize the loss and gradient to zero.
loss = 0.0
dW = np.zeros_like(W)
#############################################################################
# TODO: Compute the softmax loss and its gradient using no explicit loops. #
# Store the loss in loss and the gradient in dW. If you are not careful #
# here, it is easy to run into numeric instability. Don't forget the #
# regularization! #
#############################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
num_train = X.shape[0]
num_classes = W.shape[1]
F = X.dot(W)
exp_normalized_F = np.exp( (F.T - np.max(F, axis=1)).T )
# compute loss
sum_i = np.sum(exp_normalized_F, axis=1)
p_i = exp_normalized_F[range(num_train), y] / sum_i
L_i = - np.log(p_i)
loss = np.sum(L_i)
loss /= num_train
loss += reg*np.sum(W * W)
# compute gradient
acc_effect = (exp_normalized_F.T / sum_i).T
acc_effect[range(num_train), y] -= 1.0
dW = X.T.dot(acc_effect)
dW /= num_train
dW += 2*reg*W
pass
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
return loss, dW3.验证最佳超参数
与SVM相同
# 使用验证集来调整超参数(正则化强度和学习率)。 您应该尝试不同的学习率和正则化强度范围;
# 如果你小心,你应该能够在验证集上获得超过 0.35 的分类准确度。
from cs231n.classifiers import Softmax
results = {}
best_val = -1
best_softmax = None
################################################################################
# TODO: #
#使用验证集设置学习率和正则化强度。 这应该与您为 SVM 所做的验证相同;
#在 best_softmax 中保存最佳训练的 softmax 分类器。
################################################################################
# Provided as a reference. You may or may not want to change these hyperparameters
learning_rates = [5e-8, 5e-6]
regularization_strengths = [5e3, 5e5]
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# follow the same steps in svm.ipynb:
# first select learning rate that makes lose go down,
# then select the regularization strength by cross-validation
for lr in [5e-8, 1e-7, 5e-7, 1e-6, 5e-6]:
# instead of np.linspace(learning_rates[0], learning_rates[1], num=5)
for reg in [5e3, 7.5e3, 1e4, 2.5e4, 5e4, 7.5e4, 1e5, 2.5e5, 5e5]:
# instead of np.linspace(regularization_strengths[0], regularization_strengths[1], num=5)
softmax_clf = Softmax()
softmax_clf.train(X_train, y_train, learning_rate=lr, reg=reg, num_iters=200)
y_train_pred = softmax_clf.predict(X_train)
y_val_pred = softmax_clf.predict(X_val)
train_acc = np.mean(y_train_pred == y_train)
val_acc = np.mean(y_val_pred == y_val)
print('lr %e reg %e train accuracy: %f val accuracy: %f' % (
lr, reg, train_acc, val_acc))
if val_acc > best_val:
best_val = val_acc
best_softmax = softmax_clf
pass
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# Print out results.
for lr, reg in sorted(results):
train_accuracy, val_accuracy = results[(lr, reg)]
print('lr %e reg %e train accuracy: %f val accuracy: %f' % (
lr, reg, train_accuracy, val_accuracy))
print('best validation accuracy achieved during cross-validation: %f' % best_val)4.补充
grad_check_sparse()函数,位于:
from cs231n.gradient_check import grad_check_sparse
f = lambda w: softmax_loss_naive(w, X_dev, y_dev, 0.0)[0]
grad_numerical = grad_check_sparse(f, W, grad, 10)
原理图

其具体实现
def grad_check_sparse(f, x, analytic_grad, num_checks=10, h=1e-5):
"""
sample a few random elements and only return numerical
in this dimensions.
"""
for i in range(num_checks):
ix = tuple([randrange(m) for m in x.shape])
oldval = x[ix]
x[ix] = oldval + h # increment by h
fxph = f(x) # evaluate f(x + h)
x[ix] = oldval - h # increment by h
fxmh = f(x) # evaluate f(x - h)
x[ix] = oldval # reset
grad_numerical = (fxph - fxmh) / (2 * h)
grad_analytic = analytic_grad[ix]
rel_error = (abs(grad_numerical - grad_analytic) /
(abs(grad_numerical) + abs(grad_analytic)))
print('numerical: %f analytic: %f, relative error: %e'
%(grad_numerical, grad_analytic, rel_error))版权声明:本文为qq_42142973原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。