
#1 主成份分析和因子分析简介
主成份分析和因子分析用于将数据中多个相关的变量合并为少数几个潜在的维度(underlying dimensions)。Stata中相关命令主要包括:
- pca: principle components analysis,主成分分析
- factor:因子分析,用于提取不同类型的因子
- screeplot:根据pca或factor画出碎石图(scree graph,也叫特征值标绘图)
- rotate:使用factor命令之后,进行正交或斜交旋转
- predict:在使用pca、factor和rotate命令之后,创建因子分或符合变量。便于下一步进行建模分析
- alpha:哥伦巴哈阿尔法信度系数。如果不使用因子分析和主成份分析,而是直接将相关变量相加,则需要检验它们的alpha系数
- cluster:聚类分析
#2 例子:planets数据分析
第一步:导入数据
. cd "D:StataStatistics with STATA"
. use "D:StataStatistics with STATAplanets.dta", clear
第二步:查看数据
. des
/*
Contains data from D:StataStatistics with STATAplanets.dta
obs: 9 Solar system data
vars: 12 2 Jul 2012 06:11
---------------------------------------------------------------------------------------------
storage display value
variable name type format label variable label
---------------------------------------------------------------------------------------------
planet str7 %9s Planet
dsun float %9.0g Mean dist. sun, km*10^6
radius float %9.0g Equatorial radius in km
rings byte %8.0g ringlbl Has rings?
moons byte %8.0g Number of known moons
mass float %9.0g Mass in kilograms
density float %9.0g Mean density, g/cm^3
logdsun float %9.0g natural log dsun
lograd float %9.0g natural log radius
logmoons float %9.0g natural log (moons + 1)
logmass float %9.0g natural log mass
logdense float %9.0g natural log dense
---------------------------------------------------------------------------------------------
Sorted by: dsun
Note: Dataset has changed since last saved.
*/
第三步:PCA主成份分析
. pca rings logdsun-logdense //第4个 + 后5个变量
/*
Principal components/correlation Number of obs = 9
Number of comp. = 6
Trace = 6
Rotation: (unrotated = principal) Rho = 1.0000
--------------------------------------------------------------------------
Component | Eigenvalue Difference Proportion Cumulative
-------------+------------------------------------------------------------
Comp1 | 4.62365 3.45469 0.7706 0.7706
Comp2 | 1.16896 1.05664 0.1948 0.9654
Comp3 | .112323 .0539515 0.0187 0.9842
Comp4 | .0583717 .0217421 0.0097 0.9939
Comp5 | .0366296 .0365651 0.0061 1.0000
Comp6 | .00006454 . 0.0000 1.0000
--------------------------------------------------------------------------
Principal components (eigenvectors)
----------------------------------------------------------------------------------------
Variable | Comp1 Comp2 Comp3 Comp4 Comp5 Comp6 | Unexplained
-------------+------------------------------------------------------------+-------------
rings | 0.4554 0.0714 0.2912 0.0351 -0.8370 0.0301 | 0
logdsun | 0.3121 -0.6576 0.5930 -0.1418 0.3135 -0.0156 | 0
lograd | 0.4292 0.3455 -0.0390 -0.3216 0.2619 0.7231 | 0
logmoons | 0.4541 0.0003 -0.1567 0.8466 0.2286 0.0156 | 0
logmass | 0.3878 0.5037 0.1374 -0.2427 0.2675 -0.6682 | 0
logdense | -0.3930 0.4352 0.7201 0.3157 0.0932 0.1708 | 0
----------------------------------------------------------------------------------------
*/结果解释:
- 特征值(eigenvalue)大于1的共有两个,一个是Comp1,一个是Comp2;特征值小于1表示解释能力还不如原变量。结果通常会排除特征值小于1的成份
- Comp1 解释了 4.62/6 = 0.7706那么多标准化方差;加上Comp2,前两个主成份共解释了0.9654的标准化方差
第三步:PCF, principle component factors,主成份因子法分析。使用factor命令,加上pcf选项即可
. factor rings logdsun-logdense, pcf
/*
(obs=9)
Factor analysis/correlation Number of obs = 9
Method: principal-component factors Retained factors = 2
Rotation: (unrotated) Number of params = 11
--------------------------------------------------------------------------
Factor | Eigenvalue Difference Proportion Cumulative
-------------+------------------------------------------------------------
Factor1 | 4.62365 3.45469 0.7706 0.7706
Factor2 | 1.16896 1.05664 0.1948 0.9654
Factor3 | 0.11232 0.05395 0.0187 0.9842
Factor4 | 0.05837 0.02174 0.0097 0.9939
Factor5 | 0.03663 0.03657 0.0061 1.0000
Factor6 | 0.00006 . 0.0000 1.0000
--------------------------------------------------------------------------
LR test: independent vs. saturated: chi2(15) = 100.49 Prob>chi2 = 0.0000
Factor loadings (pattern matrix) and unique variances //主成份因子法会自动删除特征值小于1的因子
-------------------------------------------------
Variable | Factor1 Factor2 | Uniqueness
-------------+--------------------+--------------
rings | 0.9792 0.0772 | 0.0353
logdsun | 0.6710 -0.7109 | 0.0443
lograd | 0.9229 0.3736 | 0.0088
logmoons | 0.9765 0.0003 | 0.0465
logmass | 0.8338 0.5446 | 0.0082
logdense | -0.8451 0.4705 | 0.0644
-------------------------------------------------
*/
第四步:screeplot碎石图
. screeplot, yline(1)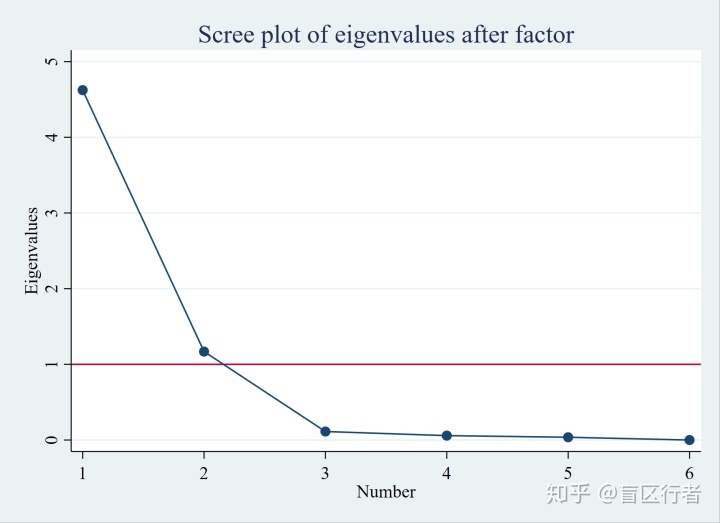
图中在特征值=1处画了一个横线,强调特征值大于1的因子才是我们想要的
第五步:旋转rotate
. rotate, promax(3) factors(2) #将
Factor analysis/correlation Number of obs = 9
Method: principal-component factors Retained factors = 2
Rotation: oblique promax (Kaiser off) Number of params = 11
--------------------------------------------------------------------------
Factor | Variance Proportion Rotated factors are correlated
-------------+------------------------------------------------------------
Factor1 | 4.12467 0.6874
Factor2 | 3.32370 0.5539
--------------------------------------------------------------------------
LR test: independent vs. saturated: chi2(15) = 100.49 Prob>chi2 = 0.0000
Rotated factor loadings (pattern matrix) and unique variances
-------------------------------------------------
Variable | Factor1 Factor2 | Uniqueness
-------------+--------------------+--------------
rings | 0.7626 0.3466 | 0.0353
logdsun | -0.1727 1.0520 | 0.0443
lograd | 0.9926 0.0060 | 0.0088
logmoons | 0.6907 0.4275 | 0.0465
logmass | 1.0853 -0.2154 | 0.0082
logdense | -0.1692 -0.8719 | 0.0644
-------------------------------------------------
Factor rotation matrix
--------------------------------
| Factor1 Factor2
-------------+------------------
Factor1 | 0.9250 0.7898
Factor2 | 0.3800 -0.6134
--------------------------------
*说明:旋转后发现rings、lograd、logmoons和logmass在Factor 1上的负载最高。和“大规模/低密度”相关
. loadingplot, factors(2) yline(0) xline(0) //将结果可视化。如下图所示
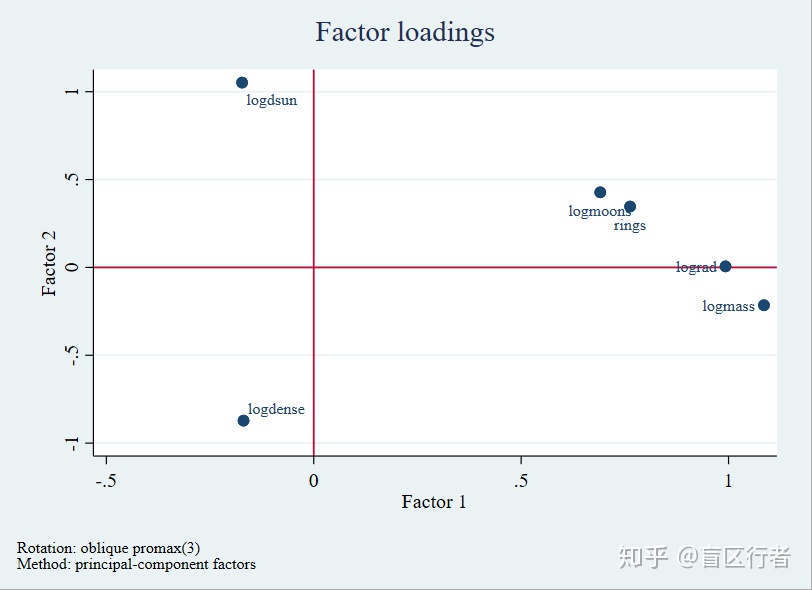
第六步:因子分factor scores
. predict f1 f2
(option regression assumed; regression scoring)
Scoring coefficients (method = regression; based on promax(3) rotated factors)
----------------------------------
Variable | Factor1 Factor2
-------------+--------------------
rings | 0.22099 0.12674
logdsun | -0.09689 0.48769
lograd | 0.30608 -0.03840
logmoons | 0.19543 0.16664
logmass | 0.34386 -0.14338
logdense | -0.01609 -0.39127
----------------------------------
. list planet f1 f2
+---------------------------------+
| planet f1 f2 |
|---------------------------------|
1. | Mercury -.9172388 -1.256881 |
2. | Venus -.5160229 -1.188757 |
3. | Earth -.3939372 -1.035242 |
4. | Mars -.6799535 -.5970106 |
5. | Jupiter 1.342658 .3841085 |
|---------------------------------|
6. | Saturn 1.184475 .9259058 |
7. | Uranus .7682409 .9347457 |
8. | Neptune .647119 .8161058 |
9. | Pluto -1.43534 1.017025 |
+---------------------------------+
.
. sum f1 f2
Variable | Obs Mean Std. Dev. Min Max
-------------+---------------------------------------------------------
f1 | 9 -3.31e-09 1 -1.43534 1.342658
f2 | 9 9.93e-09 1 -1.256881 1.017025
. corr f1 f2 //没有旋转之前,两个因子完全无关。最大方差旋转后因子之间也是无关的
(obs=9)
| f1 f2
-------------+------------------
f1 | 1.0000
f2 | 0.4974 1.0000
第七步:使用因子变量
通过因子分析得到的变量,通常会给它一个现实意义上的称呼。比如第五步中的f2,可以称为“距离远且密度低”。
然后,就可以将它当成普通的变量来使用—比如放入回归模型。
.reg f2 logdsun logra logmoons
/*
Source | SS df MS Number of obs = 9
-------------+---------------------------------- F(3, 5) = 63.61
Model | 7.79573228 3 2.59857743 Prob > F = 0.0002
Residual | .204267695 5 .040853539 R-squared = 0.9745
-------------+---------------------------------- Adj R-squared = 0.9591
Total | 7.99999997 8 .999999996 Root MSE = .20212
------------------------------------------------------------------------------
f2 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
logdsun | .4404628 .0674815 6.53 0.001 .2669961 .6139296
lograd | -.081395 .137908 -0.59 0.581 -.4358989 .2731089
logmoons | .3189279 .1950787 1.63 0.163 -.1825378 .8203937
_cons | -2.560538 1.308671 -1.96 0.108 -5.924585 .8035082
------------------------------------------------------------------------------
*/