图着色问题

“四色问题”一直是数学方面一个重要且困难的问题，直到计算机的发明才得以侧面证明，如何求一个图的着色色数，可以通过回溯法来解决。

问题描述

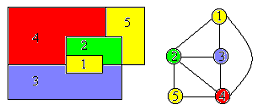
已知一个图G和m种颜色，在只准使用这m种颜色对G的结点着色的情况下，是否能使图中任何相邻的两个结点都具有不同的颜色呢？这个问题称为m-着色判定问题。可对图G着色的最小正整数m，称为图G的色数。

分析设计

图的表示我们采用二维数组邻接矩阵的形式存储。颜色我们可以使用正整数1、2、3……m的形式表示，通过一位数组x[n]来记录结点颜色，x[i]表示结点i的颜色为x[i]。

我们可以通过深度遍历的方法遍历每一个结点，颜色也从1开始试，在给每个结点确定颜色时，判断与它相邻的结点是否着色冲突：

• 都不冲突，则继续往下一个结点走；
• 存在冲突，则换一个颜色继续试；当所有颜色试完均无可行解，则回溯至上一个顶点；
• 当所有顶点都找到了一种颜色解决时，我们就可以说改图所需色数可能小于等于m。

源代码

#include <iostream>
#include <vector>

using namespace std;

vector<vector<bool> > graph;	//邻接图
vector<int> x;					//节点数组
int color;						//颜色种类

//输出结果
void print(int k) {
	for (int i = 1; i <= k; i++) 
		cout << x[i] << " ";
	cout << endl;
}

//递归算法
void MColoring(int k) {
	int j;
	while (1) {
		x[k]++;
		if (x[k] > color)
			return;
		for (j = 1; j <= k - 1; j++) 
			if (graph[k][j] && x[k] == x[j])	//存在冲突
				break;
		if (j == k)
			break;
	}
	if (k == x.size() - 1) {	//找到一种可能
		print(k);
		return;
	}
	else
		MColoring(k + 1);	//递归进入下一层
}


int main() {
	int n;
	cout << "输入图顶点数：";
	cin >> n;
	vector<vector<bool> >g(n + 1, vector<bool>(n + 1, false));	//邻接矩阵图
	cout << "输入邻接边a b：（输入0结束）" << endl;
	int a, b;
	while (cin >> a && a) {
		cin >> b;
		g[a][b] = true;
		g[b][a] = true;
	}
	graph = g;

	vector<int> t(n + 1, 0);
	x = t;
	x[1] = 1;

	cout << "输入颜色种类：";
	cin >> color;

	MColoring(1);

	system("pause");
	return 0;
}


/*
1 2
2 3
1 3
1 4
2 4
2 5
3 4
4 5
*/

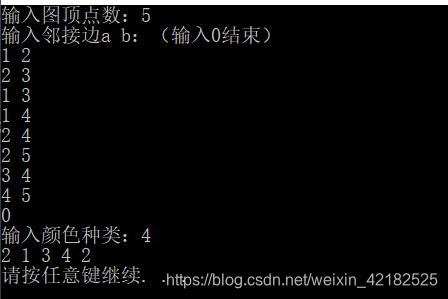
运行结果