联邦学习数学公式纯手推

=========================================================
以下每个算法都从数据、模型、代价函数以及梯度下降四方面来推导

1.逻辑回归

1.1 基本思想

经典的逻辑回归是一个二分类算法（分类标签0和1），核心思想是在线性回归的基础上加了一个sigmoid激活函数，即线性+非线性，而sigmoid函数有一个特点，所有定义域内的数值都会映射到（0，1）之间，左右都是开区间，这就类比于概率值，可以把所有的值域的数看成是预测正类的概率值，如此，则规定0.5是一个分界，高于0.5看作1类，低于0.5看作0类

1.2 sigmoid

原函数h=g(z)=1/(1+e^-z)取值范围(0,1)
导函数h’=h(1-h)取值范围(0,0.25]

2.联邦学习

2.1 背景

隐私保护、数据安全和行业竞争需求导致的“数据孤岛”问题

2.2 本质

一种分布式机器学习技术或机器学习框架，多方联合建模，数据不动模型动

2.3 目标

保证数据隐私安全以及合法合规，实现共同建模，提升AI模型的效果

2.4 分类

横向联邦学习
纵向联邦学习
联邦迁移学习（样本特征均不相同，目前落地应用较少，还只停留在学术层面）

3.横向逻辑回归

3.1 数据要求

特征相同，样本不同

3.2 应用

相同行业（金融领域）
例如：银行+监管——联合反洗钱建模

3.3 比较代价和梯度

代价函数：

	@staticmethod
    def compute_loss(values, coef, intercept):
        X, Y = load_data(values)
        batch_size = len(X)
        if batch_size == 0:
            LOGGER.warning("This partition got 0 data")
            return None
        tot_loss = np.log(1 + np.exp(np.multiply(-Y.transpose(), X.dot(coef) + intercept))).sum()
        return tot_loss

梯度：

	@staticmethod
    def compute_gradient(values, coef, intercept, fit_intercept):
        X, Y = load_data(values)
        batch_size = len(X)
        if batch_size == 0:
            LOGGER.warning("This partition got 0 data")
            return None

        d = (1.0 / (1 + np.exp(-np.multiply(Y.transpose(), X.dot(coef) + intercept))) - 1).transpose() * Y
        grad_batch = d * X
        if fit_intercept:
            grad_batch = np.c_[grad_batch, d]
        grad = sum(grad_batch)
        return grad

4.纵向逻辑回归

4.1 数据要求

样本相同，特征不同

4.2 应用

不同行业
银行+互联网——联合信贷风控建模
互联网+保险——联合权益定价建模
互联网+零售——联合客户价值建模

4.3 比较代价和梯度

代价函数：

    def compute_loss(self, data_instances, w, n_iter_, batch_index, loss_norm=None):
        """
        Compute hetero-lr loss for:
        loss = (1/N)*∑(log2 - 1/2*ywx + 1/8*(wx)^2), where y is label, w is model weight and x is features
        where (wx)^2 = (Wg * Xg + Wh * Xh)^2 = (Wg*Xg)^2 + (Wh*Xh)^2 + 2 * Wg*Xg * Wh*Xh

        Then loss = log2 - (1/N)*0.5*∑ywx + (1/N)*0.125*[∑(Wg*Xg)^2 + ∑(Wh*Xh)^2 + 2 * ∑(Wg*Xg * Wh*Xh)]

        where Wh*Xh is a table obtain from host and ∑(Wh*Xh)^2 is a sum number get from host.
        """

梯度：

    def compute_and_aggregate_forwards(self, data_instances, half_g, encrypted_half_g, batch_index,
                                       current_suffix, offset=None):
        """
        gradient = (1/N)*∑(1/2*ywx-1)*1/2yx = (1/N)*∑(0.25 * wx - 0.5 * y) * x, where y = 1 or -1
        Define wx as guest_forward or host_forward
        Define (0.25 * wx - 0.5 * y) as fore_gradient
        """

5.总结

各算法的代价函数和梯度汇总，可以进行简单的对比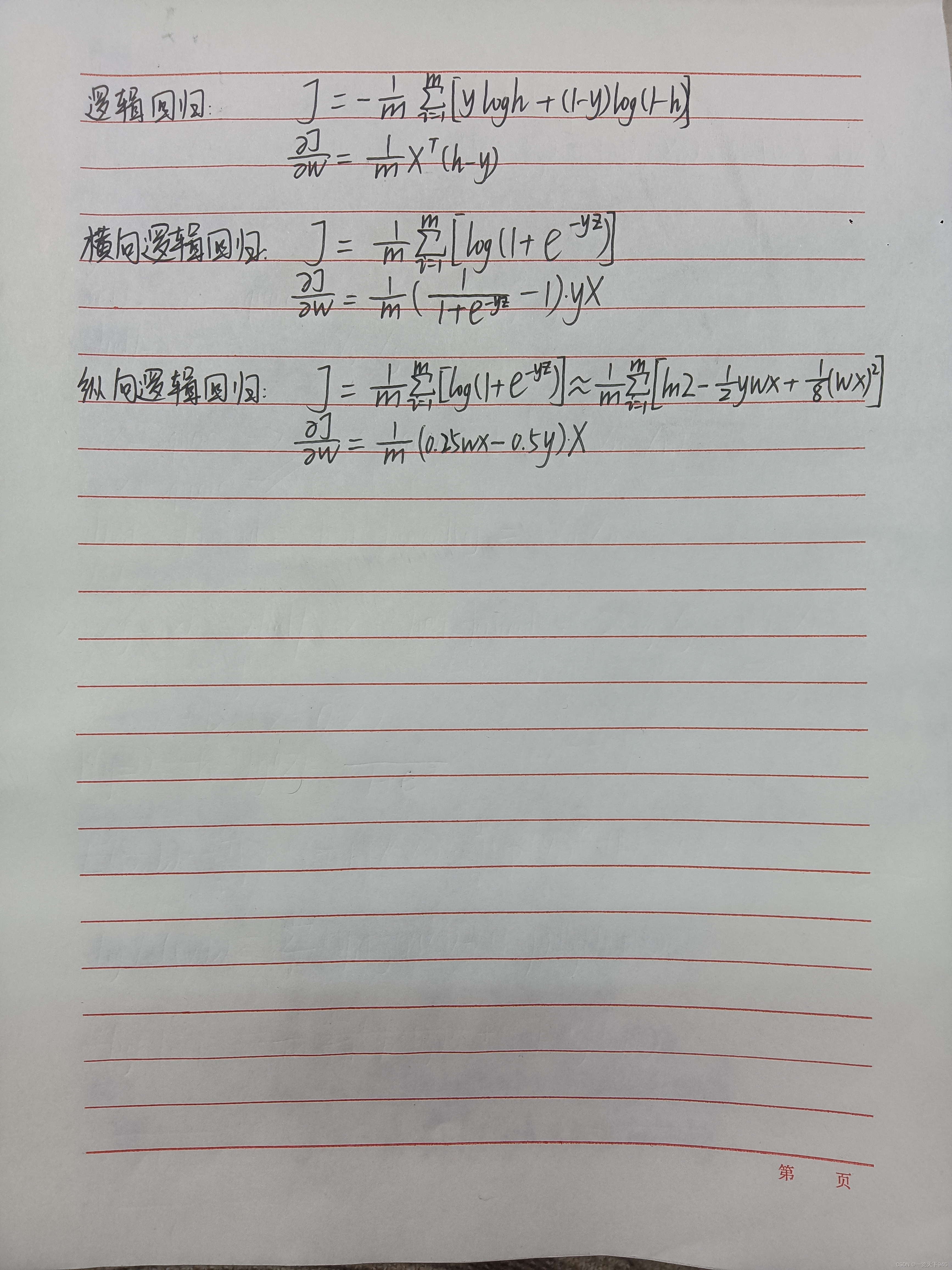

感谢大家的关注和支持，希望我写的文章能够让你们有收获。
如有不足，还请各位多多指正！