机器学习之主成分分析

主成分分析（无监督降维）

降维技术：

特征选择：从一个特征的集合里面，挑选出相应的特征。是直接抽取
特征提取：不仅仅是提取了，而是通过组合或运算的方式，从现有的特征中抽象出新的特征。注意这个新特征并不属于原本的特征集合。是需要加工
特征选择会影响模型的效果

在实验数据分析模块，数据可视化等也需要维数约简，因为一般可以可视化的数据通常为二维或者三维

主成分分析就是把原有的多个指标转化为少数几个代表性较好的综合指标，这少数几个指标能够反映原来指标大部分信息（85%以上），并且各个指标之间保持独立，避免出现重叠信息，主成分分析主要起着降维和简化数据结构的作用

有时数据处于低维时不容易分割，这时就需要升维来进行分割，例如下图：

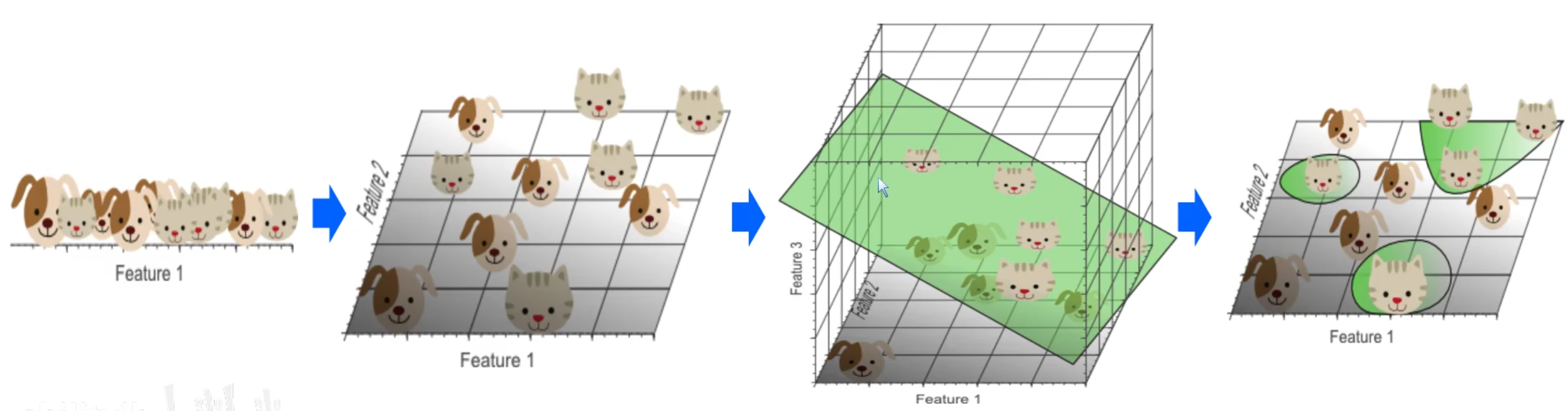
当识别小猫小狗时，在一维上只能识别出猫狗的头部，很难找出一个分割线对猫狗有一个分类，所以升到二维三维可能会更容易找出一个超维分割面来进行分类之后再映射回低维度

但是随之而来的是另外一个新问题，当升维升到一定程度之后，机器学习也会很难处理，会造成维数灾难（索引结构的性能随着维数的增大而迅速降低，在维数较高时不如顺序扫描）

降维的原理：把采集的数据从一个高维度空间映射到一个维度低得多的新空间的过程，这个过程与信息压缩概念密切相关

降维的适用原因：

高维数据的计算量相当庞大
在某些情况下高维数据导致算法具有较差的泛化能力
降维可以用于数据的解释性，为发现有意义的数据结构，并说明其用途

降维技术需要解决的问题：

消除数据冗余：去掉可导出的维（也就是去掉可以从其他属性直接或间接推导出来的属性），只保留独立维（去掉完全相关的数据）
高维数据索引
- 先进行降维
- 在降维后的子空间用一维或者多维索引技术
可能会引起信息的丢失，从而降低查询精度

例如一段数据点表示米和厘米的换算关系，所以厘米和米具有相关关系，因此，当使用降维的时候，只保留米或者厘米即可

以分类区分
- 有监督降维：对抗生成网络
- 无监督降维：主成分分析
以线性和非线性区分
- 线性降维
- 非线性降维

线性降维方法

通过特征的线性组合来降维
本质上是把数据投影到低维线性子空间
线性方法相对比较简单其容易计算
代表方法：
- 主成分分析（PCA）：把x通过变化变为更少量的特征
- 线性判别分析（LDA）
- 多维尺度变换（MDS）

主成分分析的目的与功能

目的：
- 在多变量分析中，分析者所面临的的最大难题是解决众多变量之间的关系问题
- 解决多元回归分析中的多重共线性问题
- 主成分分析可以把这众多指标所蕴含的信息压缩到少数几个成分指标，然后给出这几个只成分指标的去那种，综合到一个评价指标中
主要功能：
- 数据降维
- 变量筛选

主成分分析的数学模型：

两个向量相互正交即为相互独立

在数学上，有讨论多个指标降为上述几个综合指标的过程就叫降维，主成分分析的通常做法是，寻求原指标的p个线性组合F_i

满足如下条件：

对于一维的数据通常考察其方差，对于二维通常考察其协方差（表示变量之间的相关性），方差表示其波动程度

方差和协方差：

方差的计算公式是针对一维特征，即针对同一特征不同样本的取值来进行计算得到；而协方差则必须要求至少满足二维特征；方差是协方差的特殊情况

样本均值：

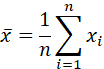
样本协方差：

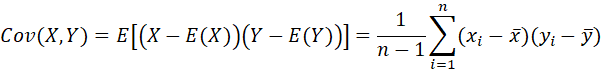
多个指标求解主成分的步骤：

一般情况下，设有n个样本，每个样本观测p个指标，将原始数据排成如下矩阵：

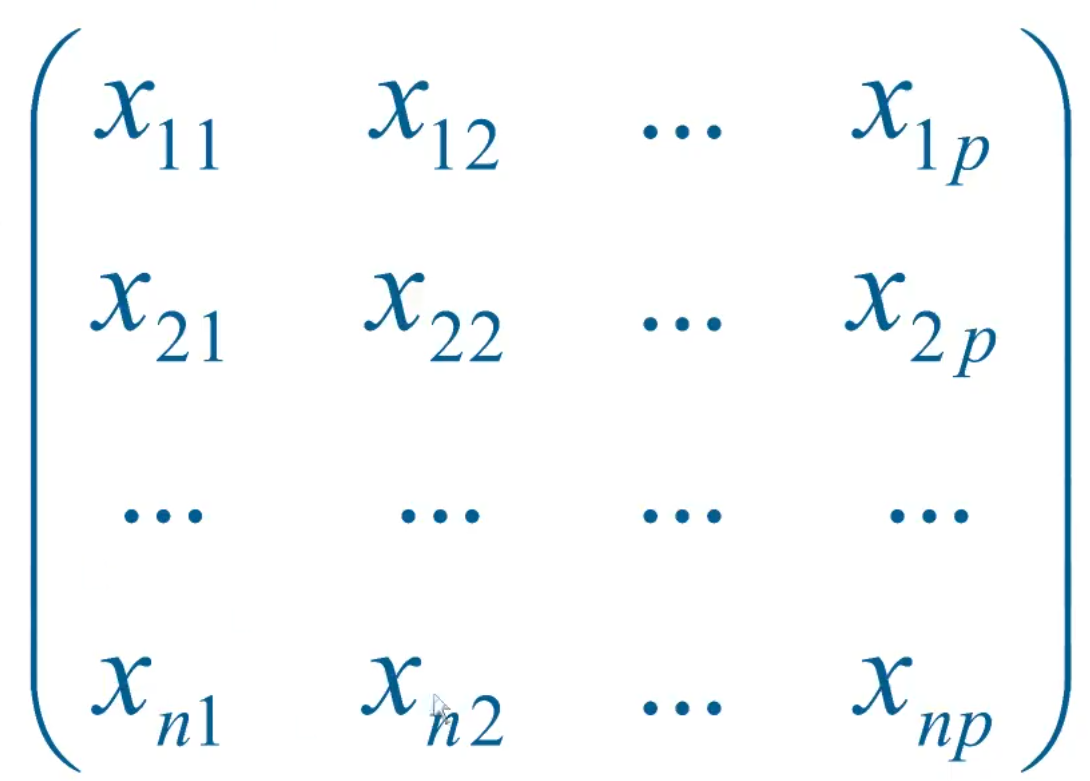
然后再按照步骤进行求解：

主成分个数的选取原则：

主要是根据累积贡献率的大小取前面m个(m<p)主成分

选取原则：

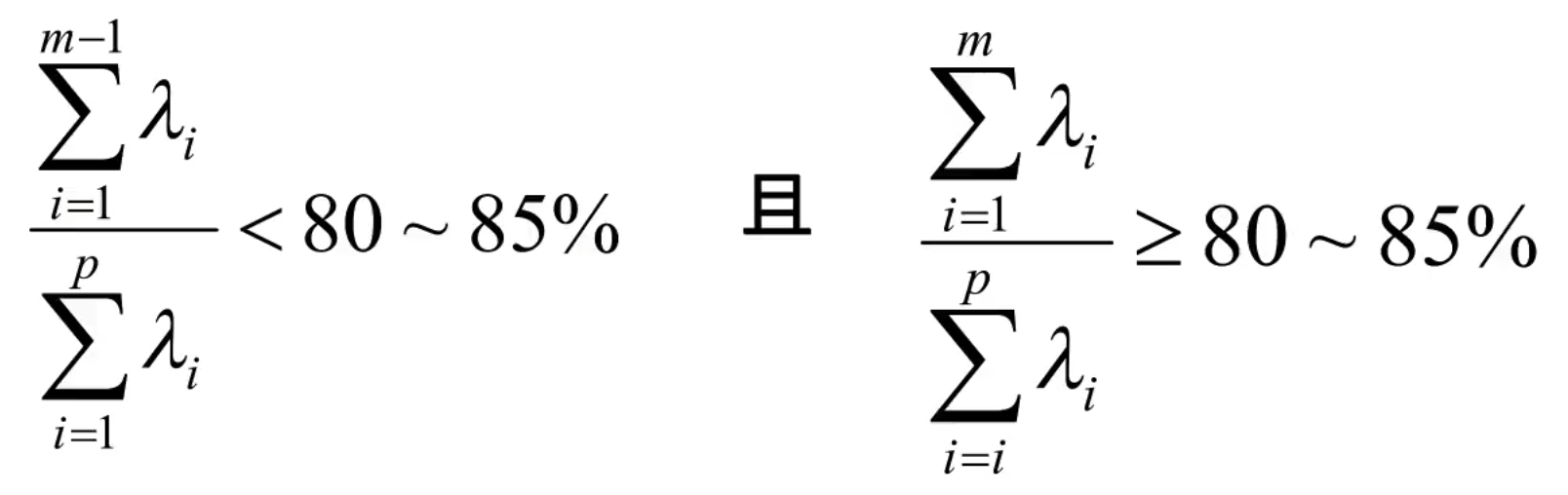
总结：

主成分是原始变量的线性组合。

第一个主成分具有最大的方差值
第二主成分试图解释数据集中的剩余方差，并且与第一主成分不相关（正交）
第三主成分试图解释前两个主成分等没解释的方差

具体计算时根据方差来计算的

具体代码实现：

非skleran实现

"""
-*- coding: utf-8 -*-
@Time    : 2021/10/24 12:24
@Author  : wcc
@FileName: principalComponentAnalysis1.py
@Software: PyCharm
@Blog    ：https://blog.csdn.net/qq_41575517?spm=1000.2115.3001.5343
"""
import numpy as np
# 此处有三个属性，分别为身高，胸围，体重
data = [[149.5, 69.5, 38.5], [162.5, 77.0, 55.5], [162.7, 78.5, 50.8], [162.2, 87.5, 65.5], [156.5, 74.5, 49.0],
        [156.1, 74.5, 45.5], [172.0, 76.5, 51.0], [173.2, 81.5, 59.5], [159.5, 74.5, 43.5], [157.7, 79.0, 53.5]]
data = np.array(data)
"""
求解协方差矩阵的步骤
1.求每个维度的平均值
2.将x的每一列减去对应维度的平均值得到一个新矩阵
3.计算协方差矩阵：
    (1)将新得到的矩阵和其转置矩阵相乘（新得到的矩阵形式为:假设有m维，则矩阵为m行n列），得到一个m*m的矩阵
    (2)然后再除以列数n
"""

averx1 = np.average(data[:, 0])
averx2 = np.average(data[:, 1])
averx3 = np.average(data[:, 2])
data[:, 0] -= averx1
data[:, 1] -= averx2
data[:, 2] -= averx3
# 得到协方差矩阵
c = (np.dot(data.T, data))/np.size(data[:, 0])
# 求协方差矩阵的特征值和和对应的特征向量
value, vector = np.linalg.eig(c)
# 根据求得的特征值判断每一个属性的方差的贡献率
# 其结果为百分数，可以舍掉百分比最小的属性，保留较大的属性，因为百分比较大的属性包含的信息更广
x1 = value[0]/np.sum(value)
x2 = value[1]/np.sum(value)
x3 = value[2]/np.sum(value)
print(x1, x2, x3)

输出：
0.8035560071904497 0.18498974697392231 0.011454245835627984

使用sklearn实现

"""
-*- coding: utf-8 -*-
@Time    : 2021/10/24 13:13
@Author  : wcc
@FileName: principalComponentAnalysis2.py
@Software: PyCharm
@Blog    ：https://blog.csdn.net/qq_41575517?spm=1000.2115.3001.5343
"""
import numpy as np
from sklearn.decomposition import PCA
data = [[149.5, 69.5, 38.5], [162.5, 77.0, 55.5], [162.7, 78.5, 50.8], [162.2, 87.5, 65.5], [156.5, 74.5, 49.0],
        [156.1, 74.5, 45.5], [172.0, 76.5, 51.0], [173.2, 81.5, 59.5], [159.5, 74.5, 43.5], [157.7, 79.0, 53.5]]
data = np.array(data)
# PCA的参数：最主要的参数是降维后需要的维度或按照提取n%的数据信息进行降维（可以为浮点数）
model = PCA(1)
model.fit(data)
# .components_:表示获取协方差矩阵的特征向量
print(model.components_)
# .explained_variance_:表示获取协方差矩阵的特征值
print(model.explained_variance_)
# .explained_variance_:表示获取协方差矩阵的特征值所占比率
print(model.explained_variance_ratio_)
# 生成降维后的数据
newData = model.transform(data)
print(newData)

输出：
[[-0.55915657 -0.42128705 -0.71404562]]
[110.00413886]
[0.80355601]
[[ 18.91238007]
 [ -3.6550838 ]
 [ -1.04283126]
 [-15.05130709]
 [  5.39436979]
 [  8.1171921 ]
 [ -5.54322239]
 [-14.39003332]
 [  7.64415101]
 [ -0.38561512]]

主成分分析的几何意义：

主成分分析本质就是特征空间的变化，将原本的特征空间压缩变换成新的特征空间，主成分分析在空间上做的就是平移旋转坐标轴
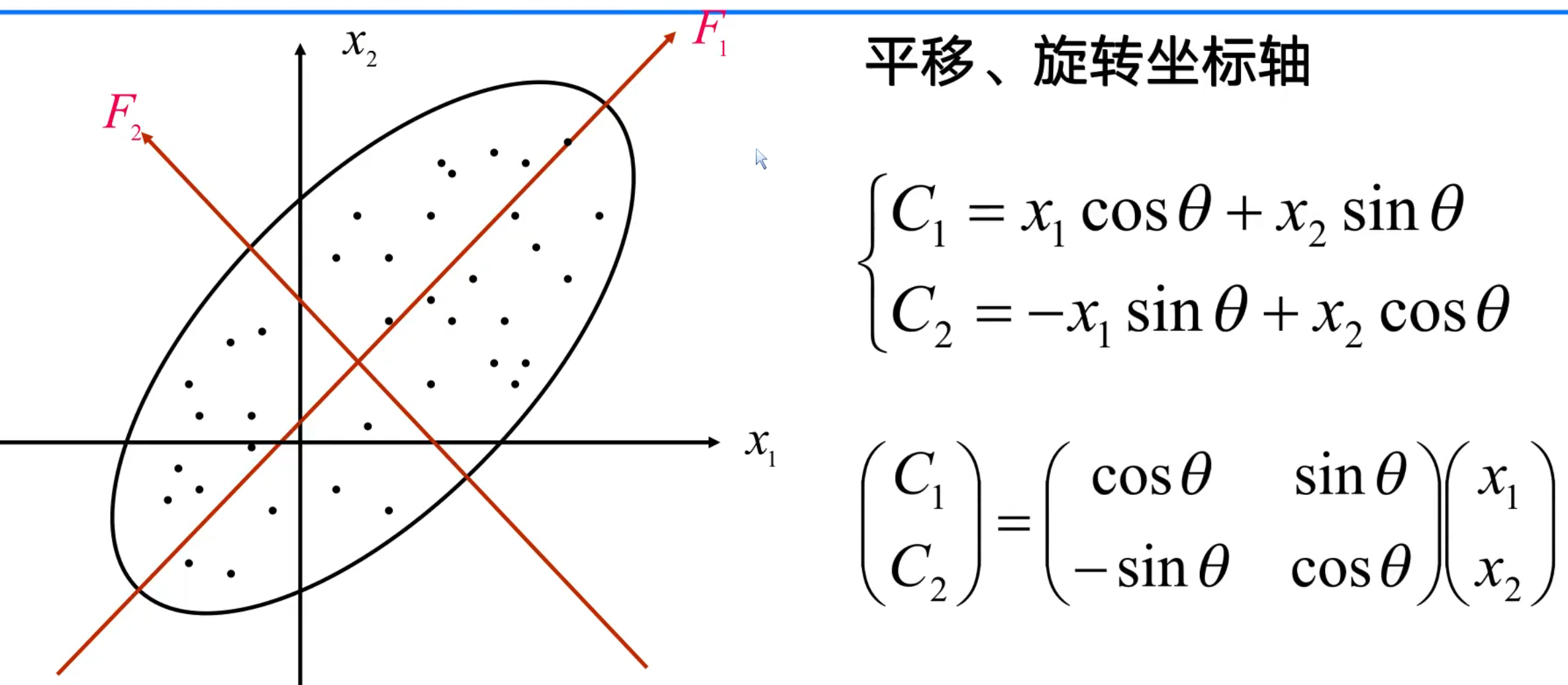
这个图的意思是，原本的坐标轴是x1，x2，现在的坐标轴为F1,F2。
如何从x1，x2轴来确定F1,F2轴？所要做的就是使得F1轴离散程度最大，即F1的方差最大，而F2则是与F1正交的轴。此处只是举了二维的例子，上升到多维也是同样的道理。
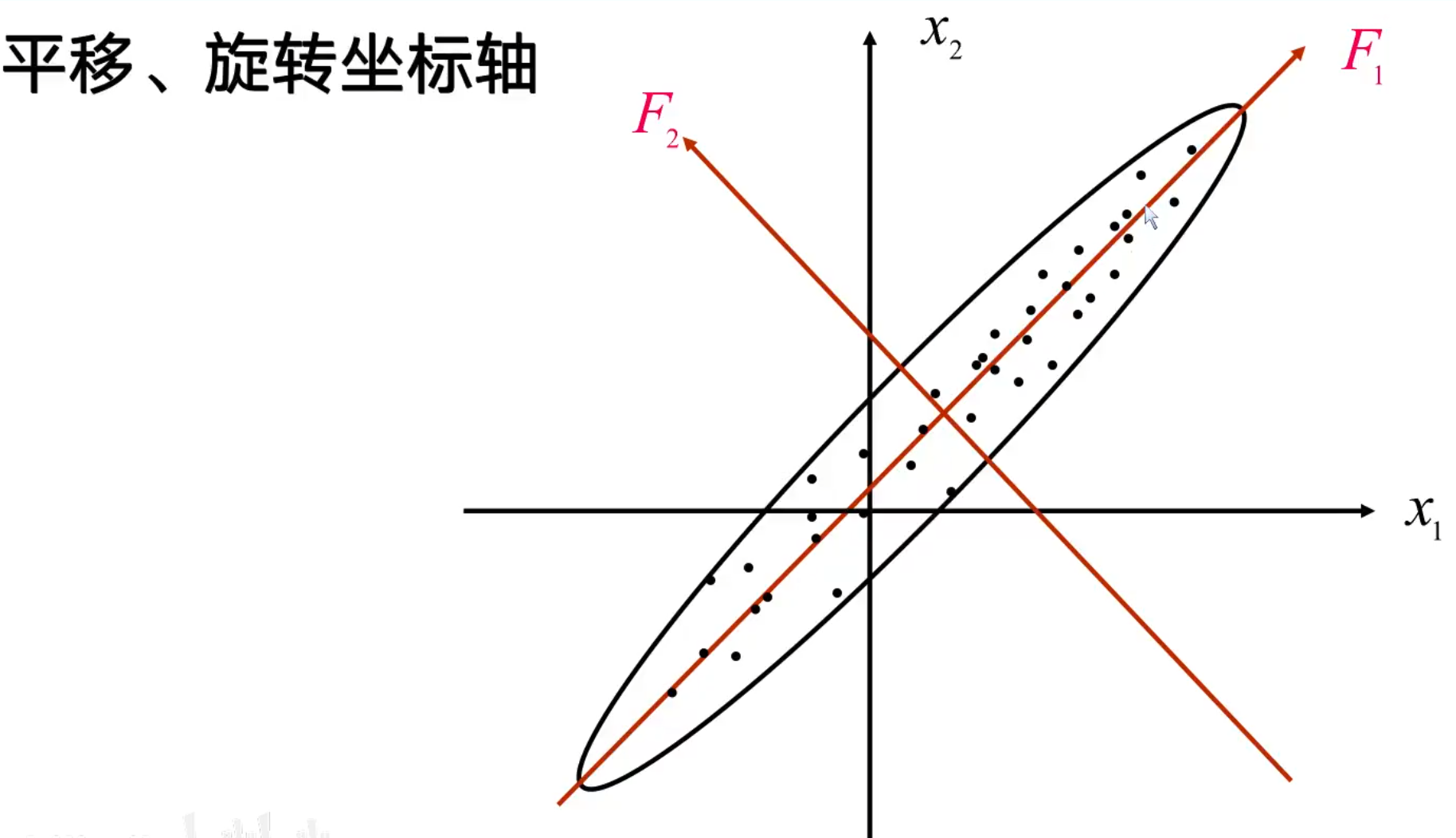
主成分分析其实就是通过坐标变换，得到一个新的坐标轴，在这个新坐标轴里面，可以把和这个数据变化关系不大的轴去掉，因为方差就表示数据的变化，所以去掉关系不大的轴就时实现了降维作用。在上图中，即使不考虑F2变量，也损失不了多少信息。从另一方面来说，去掉F2也是实现了降维。

原文链接：https://blog.csdn.net/qq_41575517/article/details/120934666