矩阵

在数学中，矩阵（Matrix）是一个按照长方阵列排列的复数或实数集合。矩阵是高等代数学中的常见工具，也常见于统计分析等应用数学学科中。 在物理学中，矩阵于电路学、力学、光学和量子物理中都有应用；计算机科学中，三维动画制作也需要用到矩阵。 矩阵的运算是数值分析领域的重要问题。将矩阵分解为简单矩阵的组合可以在理论和实际应用上简化矩阵的运算。对一些应用广泛而形式特殊的矩阵，例如稀疏矩阵和准对角矩阵，有特定的快速运算算法。

矩阵的基本运算

矩阵运算在科学计算中非常重要 ，而矩阵的基本运算包括矩阵的加法，减法，数乘，转置，共轭和共轭转置

矩阵加法

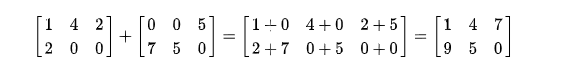
矩阵的加法满足下列运算律(A，B，C都是同型矩阵)：
A+B = B+A
（A+B）+C = A+（B+C）

矩阵减法

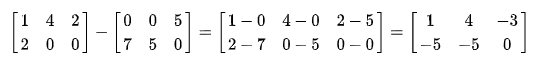
矩阵数乘

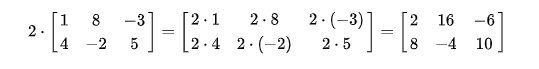
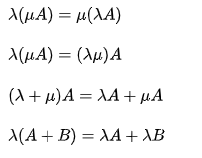
矩阵转置

把矩阵A的行和列互相交换所产生的矩阵称为A的转置矩阵(A)T ，这一过程称为矩阵的转置。
矩阵的转置满足以下运算律：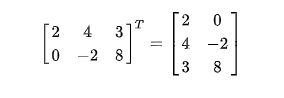

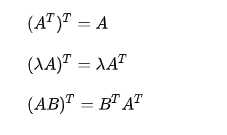
矩阵乘法

两个矩阵的乘法仅当第一个矩阵A的列数和另一个矩阵B的行数相等时才能定义。如A是m×n矩阵和B是n×p矩阵，它们的乘积C是一个m×p矩阵 。乘积：C=AB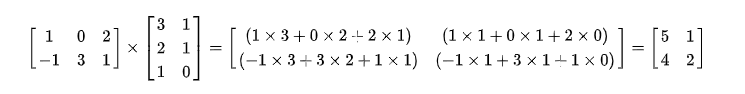

矩阵的乘法满足以下运算律：
结合律：A(BC)=(AB)C
左分配律：A(B+C)=AB+AC
右分配律：(A+B)C=AC+BC
注意：矩阵乘法不满足交换律。

矩阵代码

public class MatrixTest {

	public static void main(String[] args) {
		// TODO Auto-generated method stub
		//创建矩阵
		int[][] a = new int[3][4];
		int[][] b = new int[3][4];
		int[][] c = new int[4][4];
		//矩阵赋值
		a=Matrix_value(a);
		b=Matrix_value(b);
		//输出矩阵
		System.out.println("============== 矩阵A ==================");
		Matrix_Show(a);
		System.out.println("============== 矩阵B ==================");
		Matrix_Show(b);
		// 加法
		System.out.println("============== 矩阵A + 矩阵B ============");
		Matrix_Add(a, b);
		// 减法
		System.out.println("============== 矩阵A - 矩阵B ============");
		Matrix_Sub(a, b);
		// 乘法
		c=Matrix_value(c);
		System.out.println("============== 矩阵C ==================");
		Matrix_Show(c);
		System.out.println("============== 矩阵A * 矩阵C ============");
		Matrix_Mul(a, c);
		//数乘
		System.out.println("============== 2 * 矩阵A =================");
		Matrix_Mul(2, a);
		//转置
		System.out.println("============== 矩阵A转置 =====================");
		Matrix_Tran(a);
		//旋转
		System.out.println("============== 矩阵旋转  =====================");
		for (int i = 1; i <= 3; i++) {
			System.out.println("============== 旋转 " + i + " 次（每次旋转90度）  =====================");
			a = Matrix_Rotate(a);
			Matrix_Show(a);
		}
		//对角线之差
		System.out.println("============== 矩阵对角线之差  =====================");
		Matrix_Diag(a);
	}

	// 矩阵赋值
	public static int[][] Matrix_value(int[][] a) {
		for (int i = 0; i < a.length; i++) {
			for (int j = 0; j < a[0].length; j++) {
				a[i][j] = (int) (Math.random() * 100 + 1);
			}
		}
		return a;
	}

	// 输出矩阵
	public static void Matrix_Show(int[][] a) {
		// System.out.println(Arrays.deepToString(a));
		for (int i = 0; i < a.length; i++) {
			for (int j = 0; j < a[0].length; j++) {
				System.out.print(a[i][j] + " ");
			}
			System.out.println();
		}

	}

	// 加法
	public static void Matrix_Add(int[][] a, int[][] b) {
		int[][] result = new int[a.length][a[0].length];
		for (int i = 0; i < result.length; i++) {
			for (int j = 0; j < result[0].length; j++) {
				result[i][j] = a[i][j] + b[i][j];
			}
		}
		Matrix_Show(result);

	}

	// 减法
	public static void Matrix_Sub(int[][] a, int[][] b) {
		int[][] result = new int[a.length][a[0].length];
		for (int i = 0; i < result.length; i++) {
			for (int j = 0; j < result[0].length; j++) {
				result[i][j] = a[i][j] - b[i][j];
			}
		}
		Matrix_Show(result);

	}

	// 乘法
	public static void Matrix_Mul(int[][] a, int[][] b) {
		int[][] result = new int[a.length][b[0].length];
		for (int i = 0; i < result.length; i++) {
			for (int j = 0; j < result[0].length; j++) {
				for (int k = 0; k < b.length; k++) {
					result[i][j] += a[i][k] * b[k][j];
				}
			}
		}
		Matrix_Show(result);
	}

	// 数乘
	public static void Matrix_Mul(int n, int[][] a) {
		int[][] result = new int[a.length][a[0].length];
		for (int i = 0; i < result.length; i++) {
			for (int j = 0; j < result[0].length; j++) {
				result[i][j] = a[i][j] * n;
			}
		}
		Matrix_Show(result);
	}

	// 矩阵转置
	public static void Matrix_Tran(int[][] a) {
		int[][] result = new int[a[0].length][a.length];
		for (int i = 0; i < result.length; i++) {
			for (int j = 0; j < result[0].length; j++) {
				result[i][j] = a[j][i];
			}
		}
		Matrix_Show(result);
	}

	// 矩阵旋转
	public static int[][] Matrix_Rotate(int[][] a) {

		// 获得原矩阵的宽高
		// 外层一维数组的长度
		int w = a.length;
		// 内层一维数组的长度
		int h = a[0].length;

		// 创建一个新二维数组
		int[][] c = new int[h][w];

		// 原数组的读取位置
		int x = w - 1;
		int y = 0;

		// 将原的二维数组反转90度，赋值到新的二维数组中
		for (int i = 0; i < c.length; i++) {
			for (int j = 0; j < c[i].length; j++) {
				c[i][j] = a[x][y];
				x--;
			}

			// 换行赋值
			x = w - 1;
			y++;
		}

		// 旋转90度之后的结果
		return c;
	}

	// 矩阵对角线之差
	public static void Matrix_Diag(int[][] a) {
		// 主对角线
		int x = 0;
		// 次对角线
		int y = 0;
		// 外层一维数组的长度
		int i = 0;
		// 内层一维数组的长度
		int j = 0;
		// 求主对角线值
		while ((i < a.length) && (j < a[0].length)) {
			x += a[i][j];
			i++;
			j++;
		}
		i = 0;
		j = a[0].length - 1;
		// 求次对角线值
		while ((i < a.length) && (j >= 0)) {
			y += a[i][j];
			i++;
			j--;
		}
		System.out.println("矩阵对角线之差为 " + (x - y));
	}
}

文章图片来源
百度-矩阵