本学期的机器学习课程,作业参考了吴恩达大佬的手写数字识别实验。
以下是完成的代码:
import numpy as np
import scipy.io as sio
from scipy.optimize import fmin_cg
import matplotlib.pyplot as plt
def display_data(data, img_width=20):
"""将图像数据 data 按照矩阵形式显示出来"""
plt.figure()
# 计算数据尺寸相关数据
n_rows, n_cols = data.shape
img_height = n_cols // img_width
# 计算显示行数与列数
disp_rows = int(np.sqrt(n_rows))
disp_cols = (n_rows + disp_rows - 1) // disp_rows
# 图像行与列之间的间隔
pad = 1
disp_array = np.ones((pad + disp_rows*(img_height + pad),
pad + disp_cols*(img_width + pad)))
idx = 0
for row in range(disp_rows):
for col in range(disp_cols):
if idx > n_rows:#这里的n_rows已经更改,原值为未出现的m
break
# 复制图像块
rb = pad + row*(img_height + pad)
cb = pad + col*(img_width + pad)
disp_array[rb:rb+img_height, cb:cb+img_width] = data[idx].reshape((img_height, -1), order='F')
# 获得图像块的最大值,对每个训练样本分别归一化
max_val = np.abs(data[idx].max())
disp_array[rb:rb+img_height, cb:cb+img_width] /= max_val
idx += 1
plt.imshow(disp_array)
plt.gray()
plt.axis('off')
plt.savefig('data-array.png', dpi=150)
plt.show()
def nn_cost_function(nn_params, *args):
"""神经网络的损失函数"""
# Unpack parameters from *args
input_layer_size, hidden_layer_size, num_labels, lmb, X, y = args
# Unroll weights of neural networks from nn_params
Theta1 = nn_params[:hidden_layer_size*(input_layer_size + 1)]
Theta1 = Theta1.reshape((hidden_layer_size, input_layer_size + 1))
Theta2 = nn_params[hidden_layer_size*(input_layer_size + 1):]
Theta2 = Theta2.reshape((num_labels, hidden_layer_size + 1))
# 设置变量
m = X.shape[0]
# You need to return the following variable correctly
J = 0.0
y=y.reshape([len(y),1])
tem_y=np.zeros([X.shape[0],num_labels])
for i in range(y.shape[0]):
tem_y[i,y[i,0]-1]=1
# ====================== 你的代码 ======================
z1=np.dot(np.c_[np.ones(X.shape[0]),X],np.transpose(Theta1))
h1=sigmoid(z1)
z2=np.dot(np.c_[np.ones(h1.shape[0]),h1],np.transpose(Theta2))
h2=sigmoid(z2)
# 计算损失函数J的值
J=np.sum(np.sum(-tem_y*np.log(h2)-(1-tem_y)*np.log(1-h2)))/m+lmb/2/m*(np.sum(np.sum(Theta1[:,1:]*Theta1[:,1:]))+np.sum(np.sum(Theta2[:,1:]*Theta2[:,1:])))
# ======================================================
return J
def nn_grad_function(nn_params, *args):
"""神经网络的损失函数梯度计算 """
# 获得参数信息
input_layer_size, hidden_layer_size, num_labels, lmb, X, y = args
# 得到各个参数的权重值
Theta1 = nn_params[:hidden_layer_size*(input_layer_size + 1)]
Theta1 = Theta1.reshape((hidden_layer_size, input_layer_size + 1))
Theta2 = nn_params[hidden_layer_size*(input_layer_size + 1):]
Theta2 = Theta2.reshape((num_labels, hidden_layer_size + 1))
# 设置变量
m = X.shape[0]
# ====================== 你的代码 =====================
label_y=np.zeros([m,num_labels])
y=y.reshape([len(y),1])
for i in range(y.shape[0]):
label_y[i,y[i,0]-1]=1
z1=np.dot(np.c_[np.ones(X.shape[0]),X],np.transpose(Theta1))
h1=sigmoid(z1)
z2=np.dot(np.c_[np.ones(h1.shape[0]),h1],np.transpose(Theta2))
h2=sigmoid(z2)
derta_3=h2-label_y
derta_2=np.dot(derta_3*sigmoid_gradient(z2),Theta2[:,1:])
derta_theta1=np.dot(np.transpose(derta_2),np.c_[np.ones(X.shape[0]),X])
derta_theta2=np.dot(np.transpose(derta_3),np.c_[np.ones(h1.shape[0]),h1])
Theta1_grad=derta_theta1/m
Theta2_grad=derta_theta2/m
# 计算Theta1,Theta2的梯度值
Theta1_grad[:,1:]=Theta1_grad[:,1:]+lmb/m*Theta1[:,1:]
Theta2_grad[:,1:]=Theta2_grad[:,1:]+lmb/m*Theta2[:,1:]
#Theta2_grad=np.dot(derta*sigmoid_gradient(z2),h1)
# =====================================================
grad = np.hstack((Theta1_grad.flatten(), Theta2_grad.flatten()))
return grad
def predict(Theta1, Theta2, X):
"""模型预测"""
m = X.shape[0]
# num_labels = Theta2.shape[0]
p = np.zeros((m,1), dtype=int)
# ====================== 你的代码============================
# 神经网络模型预测
z1=np.dot(np.c_[np.ones(X.shape[0]),X],np.transpose(Theta1))
h1=sigmoid(z1)
z2=np.dot(np.c_[np.ones(h1.shape[0]),h1],np.transpose(Theta2))
h2=sigmoid(z2)
# ============================================================
# print(h1.shape, h2.shape)
p = np.argmax(h2, axis=1) + 1.0
return p
def sigmoid(z):
"""Sigmoid 函数"""
return 1.0/(1.0 + np.exp(-np.asarray(z)))
def sigmoid_gradient(z):
"""计算Sigmoid 函数的梯度"""
g = np.zeros_like(z)
# ====================== 你的代码 ======================
# 计算Sigmoid 函数的梯度g的值
dz=sigmoid(z)
g=dz*(1-dz)
# =======================================================
return g
def rand_initialize_weights(L_in, L_out):
""" 初始化网络层权重参数"""
# You need to return the following variables correctly
W = np.zeros((L_out, 1 + L_in))
# ====================== 你的代码 ======================
#初始化网络层的权重参数
W=(np.random.random(size=W.shape)-0.5)*0.24
# ======================================================
return W
def debug_initialize_weights(fan_out, fan_in):
"""Initalize the weights of a layer with
fan_in incoming connections and
fan_out outgoing connection using a fixed strategy."""
W = np.linspace(1, fan_out*(fan_in+1), fan_out*(fan_in+1))
W = 0.1*np.sin(W).reshape(fan_out, fan_in + 1)
return W
def compute_numerical_gradient(cost_func, theta):
"""Compute the numerical gradient of the given cost_func
at parameter theta"""
numgrad = np.zeros_like(theta)
perturb = np.zeros_like(theta)
eps = 1.0e-4
for idx in range(len(theta)):
perturb[idx] = eps
loss1 = cost_func(theta - perturb)
loss2 = cost_func(theta + perturb)
numgrad[idx] = (loss2 - loss1)/(2*eps)
perturb[idx] = 0.0
return numgrad
def check_nn_gradients(lmb=0.0):
"""Creates a small neural network to check the backgropagation
gradients."""
input_layer_size, hidden_layer_size = 3, 5
num_labels, m = 3, 5
Theta1 = debug_initialize_weights(hidden_layer_size, input_layer_size)
Theta2 = debug_initialize_weights(num_labels, hidden_layer_size)
X = debug_initialize_weights(m, input_layer_size - 1)
y = np.array([1 + (t % num_labels) for t in range(m)])
nn_params = np.hstack((Theta1.flatten(), Theta2.flatten()))
cost_func = lambda x: nn_cost_function(x,
input_layer_size,
hidden_layer_size,
num_labels, lmb, X, y)
grad = nn_grad_function(nn_params,
input_layer_size, hidden_layer_size,
num_labels, lmb, X, y)
numgrad = compute_numerical_gradient(cost_func, nn_params)
print(np.vstack((numgrad, grad)).T, np.sum(np.abs(numgrad - grad)))
print('The above two columns you get should be very similar.')
print('(Left-Your Numerical Gradient, Right-Analytical Gradient)')
# Parameters
input_layer_size = 400 # 20x20 大小的输入图像,图像内容为手写数字
hidden_layer_size = 25 # 25 hidden units
num_labels = 10 # 10 类标号 从1到10
# =========== 第一部分 ===============
# 加载训练数据
print("Loading and Visualizing Data...")
data = sio.loadmat('D:/360安全浏览器下载/资料文件/大三上/机器学习/神经网络/data/data6559/NN_data.mat')
X, y = data['X'], data['y']
m = X.shape[0]
# 随机选取100个数据显示
rand_indices = np.array(range(m))
np.random.shuffle(rand_indices)
X_sel = X[rand_indices[:100]]
display_data(X_sel)
# =========== 第二部分 ===============
print('Loading Saved Neural Network Parameters ...')
# Load the weights into variables Theta1 and Theta2
data = sio.loadmat('D:/360安全浏览器下载/资料文件/大三上/机器学习/神经网络/data/data6559/NN_weights.mat')
Theta1, Theta2 = data['Theta1'], data['Theta2']
#print(Theta1.shape,hidden_layer_size,input_layer_size + 1)
#print(Theta2.shape,num_labels, hidden_layer_size + 1)
# ================ Part 3: Compute Cost (Feedforward) ================
# To the neural network, you should first start by implementing the
# feedforward part of the neural network that returns the cost only. You
# should complete the code in nnCostFunction.m to return cost. After
# implementing the feedforward to compute the cost, you can verify that
# your implementation is correct by verifying that you get the same cost
# as us for the fixed debugging parameters.
#
# We suggest implementing the feedforward cost *without* regularization
# first so that it will be easier for you to debug. Later, in part 4, you
# will get to implement the regularized cost.
print('Feedforward Using Neural Network ...')
# Weight regularization parameter (we set this to 0 here).
lmb = 0.0#正则化项
nn_params = np.hstack((Theta1.flatten(), Theta2.flatten()))
J = nn_cost_function(nn_params,
input_layer_size, hidden_layer_size,
num_labels, lmb, X, y)
print('Cost at parameters (loaded from PRML_NN_weights): %f ' % J)
print('(this value should be about 0.287629)')
# =============== Part 4: Implement Regularization ===============
print('Checking Cost Function (w/ Regularization) ... ')
lmb = 1.0
J = nn_cost_function(nn_params,
input_layer_size, hidden_layer_size,
num_labels, lmb, X, y)
print('Cost at parameters (loaded from PRML_NN_weights): %f ' % J)
print('(this value should be about 0.383770)')
# ================ Part 5: Sigmoid Gradient ================
print('Evaluating sigmoid gradient...')
g = sigmoid_gradient([1, -0.5, 0, 0.5, 1])
print('Sigmoid gradient evaluated at [1 -0.5 0 0.5 1]: ', g)
# ================ Part 6: Initializing Pameters ================
print('Initializing Neural Network Parameters ...')
initial_Theta1 = rand_initialize_weights(input_layer_size, hidden_layer_size)
initial_Theta2 = rand_initialize_weights(hidden_layer_size, num_labels)
# Unroll parameters
initial_nn_params = np.hstack((initial_Theta1.flatten(),
initial_Theta2.flatten()))
# =============== Part 7: Implement Backpropagation ===============
print('Checking Backpropagation... ')
# Check gradients by running checkNNGradients
check_nn_gradients()
# =============== Part 8: Implement Regularization ===============
print('Checking Backpropagation (w/ Regularization) ... ')
# Check gradients by running checkNNGradients
lmb = 3.0
check_nn_gradients(lmb)
# =================== Part 8: Training NN ===================
print('Training Neural Network...')
lmb, maxiter = 1.0, 50
args = (input_layer_size, hidden_layer_size, num_labels, lmb, X, y)
nn_params, cost_min, _, _, _ = fmin_cg(nn_cost_function,
initial_nn_params,
fprime=nn_grad_function,
args=args,
maxiter=maxiter,
full_output=True)
Theta1 = nn_params[:hidden_layer_size*(input_layer_size + 1)]
Theta1 = Theta1.reshape((hidden_layer_size, input_layer_size + 1))
Theta2 = nn_params[hidden_layer_size*(input_layer_size + 1):]
Theta2 = Theta2.reshape((num_labels, hidden_layer_size + 1))
# ================= Part 9: Implement Predict =================
pred = predict(Theta1, Theta2, X)
# print(pred.shape, y.shape)
# print(np.hstack((pred, y)))
print('Training Set Accuracy:', np.mean(pred == y[:, 0])*100.0)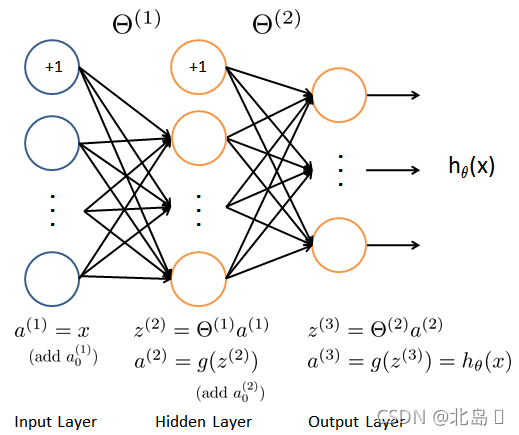
涉及的参数大致如图。
文中涉及的文件已经以资源的形式发出,可以到我的主页去找。
版权声明:本文为weixin_52255304原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。